Apa rumus dari energi kinetik? – www.sridianti.com

Energi kinetik adalah salah satu konsep dasar dalam fisika yang menggambarkan energi yang dimiliki oleh suatu objek karena gerakannya. Dalam artikel ini, kita akan membahas secara mendetail tentang rumus energi kinetik, termasuk penjelasan tentang variabel yang terlibat, derivasi rumus, serta aplikasi dan contoh penggunaannya dalam berbagai konteks.

1. Rumus Energi Kinetik

Rumus untuk menghitung energi kinetik (EK) dari suatu objek adalah sebagai berikut:

$EK = \frac{1}{2} mv^2$

Di mana:

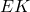$EK$ = Energi kinetik (dalam joule, J)
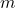$m$ = Massa objek (dalam kilogram, kg)
$v$ = Kecepatan objek (dalam meter per detik, m/s)

2. Penjelasan Variabel dalam Rumus

a. Massa (m)

Massa adalah ukuran jumlah materi dalam suatu objek. Dalam konteks energi kinetik, massa berperan penting karena semakin besar massa suatu objek, semakin besar energi kinetiknya pada kecepatan yang sama. Massa diukur dalam satuan kilogram (kg) dalam sistem internasional (SI).

b. Kecepatan (v)

Kecepatan adalah ukuran seberapa cepat suatu objek bergerak. Dalam rumus energi kinetik, kecepatan dikuadratkan ( $v^2$ ), yang menunjukkan bahwa energi kinetik meningkat secara signifikan dengan peningkatan kecepatan. Kecepatan diukur dalam satuan meter per detik (m/s).

3. Derivasi Rumus Energi Kinetik

Rumus energi kinetik dapat diturunkan dari hukum Newton dan konsep kerja. Berikut adalah langkah-langkah untuk memahami derivasi rumus tersebut:

1. Hukum Newton Kedua: Hukum ini menyatakan bahwa gaya ( $F$ ) yang bekerja pada suatu objek sama dengan massa ( $m$ ) objek dikalikan dengan percepatan ( $a$ ):

$F = ma$

2. Kerja (W): Kerja yang dilakukan pada objek sama dengan perubahan energi kinetik objek. Kerja dapat didefinisikan sebagai gaya dikalikan dengan jarak ( $d$ ) yang ditempuh dalam arah gaya:

$W = F \cdot d$

3. Menghubungkan Gaya dan Percepatan: Dengan mengganti gaya dalam persamaan kerja dengan hukum Newton, kita mendapatkan:

$W = mad$

4. Menggunakan Persamaan Kinematika: Dari kinematika, kita tahu bahwa percepatan ( $a$ ) dapat dinyatakan sebagai perubahan kecepatan ( $\Delta v$ ) dibagi dengan waktu ( $t$ ):

$a = \frac{\Delta v}{t}$

5. Menghitung Jarak: Jarak yang ditempuh selama percepatan dapat dinyatakan sebagai:

$d = \frac{1}{2} a t^2$

6. Mengganti dalam Persamaan Kerja: Dengan mengganti $a$ dan $d$ dalam persamaan kerja, kita mendapatkan:

$W = m \left(\frac{\Delta v}{t}\right) \left(\frac{1}{2} a t^2\right)$

7. Menyederhanakan: Setelah menyederhanakan, kita mendapatkan:

$W = \frac{1}{2} mv^2$

Dari sini, kita dapat menyimpulkan bahwa kerja yang dilakukan pada objek sama dengan perubahan energi kinetik, sehingga kita mendapatkan rumus energi kinetik:

$EK = \frac{1}{2} mv^2$

4. Aplikasi Rumus Energi Kinetik

Rumus energi kinetik memiliki banyak aplikasi dalam berbagai bidang, termasuk:

a. Transportasi

Dalam industri transportasi, rumus energi kinetik digunakan untuk menghitung energi yang dimiliki oleh kendaraan yang bergerak. Misalnya, insinyur dapat menggunakan rumus ini untuk merancang sistem pengereman yang efektif dengan mempertimbangkan energi kinetik kendaraan.

b. Olahraga

Dalam olahraga, atlet dan pelatih dapat menggunakan rumus energi kinetik untuk menganalisis performa atlet. Misalnya, pelari dapat menghitung energi kinetik mereka saat berlari untuk memahami seberapa efisien mereka bergerak.

c. Fisika dan Teknik

Dalam fisika dan teknik, rumus energi kinetik digunakan untuk menganalisis gerakan objek dan sistem mekanis. Ini membantu insinyur merancang mesin dan perangkat yang efisien.

5. Contoh Penggunaan Rumus Energi Kinetik

a. Contoh 1: Mobil yang Melaju

Misalkan sebuah mobil memiliki massa 1000 kg dan bergerak dengan kecepatan 20 m/s. Energi kinetik mobil tersebut dapat dihitung sebagai berikut:

$EK = \frac{1}{2} mv^2 = \frac{1}{2} \times 1000 \, \text{kg} \times (20 \, \text{m/s})^2 = \frac{1}{2} \times 1000 \times 400 = 200000 \, \text{J}$

Jadi, energi kinetik mobil tersebut adalah 200.000 joule.

b. Contoh 2: Bola yang Dilempar

Misalkan sebuah bola memiliki massa 0,5 kg dan dilempar dengan kecepatan 10 m/s. Energi kinetik bola tersebut dapat dihitung sebagai berikut:

$EK = \frac{1}{2} mv^2 = \frac{1}{2} \times 0,5 \, \text{kg} \times (10 \, \text{m/s})^2 = \frac{1}{2} \times 0,5 \times 100 = 25 \, \text{J}$

Jadi, energi kinetik bola tersebut adalah 25 joule.

6. Kesimpulan

Rumus energi kinetik, yaitu $EK = \frac{1}{2} mv^2$ , adalah alat penting dalam fisika yang digunakan untuk menghitung energi yang dimiliki oleh suatu objek karena gerakannya. Dengan memahami variabel yang terlibat, derivasi rumus, serta aplikasi dan contoh penggunaannya, kita dapat lebih menghargai konsep energi kinetik dan perannya dalam berbagai aspek kehidupan. Energi kinetik tidak hanya merupakan konsep teoritis, tetapi juga memiliki aplikasi praktis yang signifikan dalam bidang transportasi, olahraga, teknik, dan banyak lagi. Dengan demikian, pemahaman tentang energi kinetik dan rumusnya sangat penting dalam studi fisika dan aplikasinya dalam dunia nyata.

√ Apa rumus dari energi kinetik?