Percepatan adalah salah satu konsep dasar dalam fisika yang menggambarkan perubahan kecepatan suatu objek dalam satuan waktu tertentu. Dalam konteks ini, percepatan dapat didefinisikan sebagai laju perubahan kecepatan. Untuk memahami lebih dalam tentang percepatan, kita perlu membahas rumus-rumus yang terkait, jenis-jenis percepatan, serta aplikasinya dalam berbagai situasi fisik. Artikel ini akan menjelaskan secara mendetail tentang rumus percepatan, termasuk penjelasan tentang variabel yang terlibat dan contoh penerapannya.
1. Definisi Percepatan
Percepatan adalah besaran vektor yang menunjukkan perubahan kecepatan suatu objek per satuan waktu. Dalam istilah matematis, percepatan dapat dinyatakan dengan rumus:
![]()
Di mana:
 = percepatan (dalam satuan meter per detik kuadrat, m/s²)
= percepatan (dalam satuan meter per detik kuadrat, m/s²)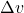 = perubahan kecepatan (dalam satuan meter per detik, m/s)
= perubahan kecepatan (dalam satuan meter per detik, m/s)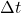 = perubahan waktu (dalam satuan detik, s)
= perubahan waktu (dalam satuan detik, s)
2. Penjelasan Variabel dalam Rumus
a. Perubahan Kecepatan (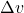 )
)
Perubahan kecepatan (![]() ) adalah selisih antara kecepatan akhir (
) adalah selisih antara kecepatan akhir (![]() ) dan kecepatan awal (
) dan kecepatan awal (![]() ) dari suatu objek. Ini dapat dinyatakan dengan rumus:
) dari suatu objek. Ini dapat dinyatakan dengan rumus:
![]()
Di mana:
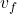 = kecepatan akhir (m/s)
= kecepatan akhir (m/s)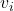 = kecepatan awal (m/s)
= kecepatan awal (m/s)
b. Perubahan Waktu (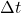 )
)
Perubahan waktu (![]() ) adalah selisih antara waktu akhir (
) adalah selisih antara waktu akhir (![]() ) dan waktu awal (
) dan waktu awal (![]() ). Ini dapat dinyatakan dengan rumus:
). Ini dapat dinyatakan dengan rumus:
![]()
Di mana:
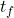 = waktu akhir (s)
= waktu akhir (s)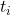 = waktu awal (s)
= waktu awal (s)
3. Rumus Percepatan dalam Berbagai Situasi
a. Percepatan Konstan
Jika percepatan suatu objek konstan, rumus percepatan tetap berlaku. Dalam hal ini, kita dapat menggunakan rumus kinematika untuk menghitung jarak yang ditempuh oleh objek selama periode waktu tertentu. Rumus yang digunakan adalah:
![]()
Di mana:
 = jarak yang ditempuh (m)
= jarak yang ditempuh (m)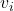 = kecepatan awal (m/s)
= kecepatan awal (m/s)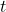 = waktu (s)
= waktu (s) = percepatan (m/s²)
= percepatan (m/s²)
b. Percepatan dalam Gerakan Vertikal
Dalam gerakan vertikal, seperti jatuh bebas, percepatan yang dialami objek adalah percepatan gravitasi (![]() ), yang memiliki nilai sekitar
), yang memiliki nilai sekitar ![]() di permukaan bumi. Dalam hal ini, rumus percepatan dapat digunakan untuk menghitung kecepatan akhir objek yang jatuh bebas:
di permukaan bumi. Dalam hal ini, rumus percepatan dapat digunakan untuk menghitung kecepatan akhir objek yang jatuh bebas:
![]()
c. Percepatan dalam Gerakan Melingkar
Dalam gerakan melingkar, percepatan juga dapat dinyatakan dalam bentuk percepatan sentripetal (![]() ), yang diperlukan untuk menjaga objek bergerak dalam lintasan melingkar. Rumus percepatan sentripetal adalah:
), yang diperlukan untuk menjaga objek bergerak dalam lintasan melingkar. Rumus percepatan sentripetal adalah:
![]()
Di mana:
 = kecepatan linear objek (m/s)
= kecepatan linear objek (m/s) = jari-jari lintasan melingkar (m)
= jari-jari lintasan melingkar (m)
4. Contoh Penerapan Rumus Percepatan
Contoh 1: Percepatan Konstan
Misalkan sebuah mobil bergerak dengan kecepatan awal ![]() dan setelah 5 detik kecepatannya menjadi
dan setelah 5 detik kecepatannya menjadi ![]() . Hitunglah percepatan mobil tersebut.
. Hitunglah percepatan mobil tersebut.
![]()
![]()
![]()
Contoh 2: Jarak yang Ditempuh
Menggunakan contoh yang sama, kita dapat menghitung jarak yang ditempuh mobil selama 5 detik.
![]()
![]()
![]()
![]()
5. Kesimpulan
Rumus percepatan adalah alat penting dalam fisika yang digunakan untuk menggambarkan perubahan kecepatan suatu objek dalam satuan waktu tertentu. Dengan memahami rumus dan variabel yang terlibat, kita dapat menganalisis berbagai situasi fisik, baik dalam gerakan lurus maupun gerakan melingkar. Percepatan memiliki aplikasi yang luas dalam berbagai bidang, termasuk teknik, olahraga, dan ilmu pengetahuan. Dengan demikian, pemahaman yang baik tentang percepatan dan rumusnya sangat penting untuk mempelajari dinamika gerakan