Acceleration is a fundamental concept in physics that describes the rate of change of an object’s velocity over time. It is a vector quantity, meaning it has both magnitude (how much the velocity changes) and direction (in which the velocity changes). Acceleration occurs when an object’s velocity changes due to an increase or decrease in speed, or a change in direction.

This article will explore what acceleration is, the different types of acceleration, the relationship between acceleration, velocity, and time, and provide examples to demonstrate how acceleration works in real-life scenarios.
What is Acceleration?
In physics, acceleration is defined as the change in an object’s velocity per unit time. If an object speeds up, slows down, or changes direction, it is said to be accelerating. Mathematically, acceleration is expressed as:

Where:
- a is acceleration,
- Δv is the change in velocity,
- Δt is the time interval over which the velocity changes.
The SI unit for acceleration is meters per second squared (m/s2), which describes how much an object’s velocity changes every second. For instance, if a car accelerates at 5 m/s2, its speed increases by 5 m/s every second.
Types of Acceleration
- Uniform Acceleration
- Non-uniform Acceleration
- Centripetal Acceleration
1. Uniform Acceleration
Uniform acceleration occurs when an object’s velocity changes at a constant rate. This means that the object’s acceleration does not vary over time. A classic example of uniform acceleration is an object in free fall, where gravity accelerates it at a constant rate, assuming no air resistance.
Example:
A car accelerates from rest at a constant rate of 2 m/s2. After 5 seconds, we can calculate the car’s velocity using the equation:
v=u+at
Where:
- v is the final velocity,
- u is the initial velocity (which is 0, since the car starts from rest),
- a is the acceleration (2 m/s2),
- t is the time (5 seconds).
v=0+(2×5)=10 m/s
Thus, after 5 seconds, the car is moving at a speed of 10 m/s.
2. Non-uniform Acceleration
In non-uniform acceleration, the rate of change of velocity is not constant. This means the object accelerates at varying rates over time. This type of acceleration is more common in real-world scenarios, where forces acting on an object may not be uniform. For instance, a car in traffic will accelerate and decelerate at different rates depending on traffic conditions.
Example:
A cyclist moves along a path where they initially accelerate slowly and then pedal harder, increasing their rate of acceleration over time. Their speed doesn’t increase uniformly, as it depends on the cyclist’s changing effort and the terrain.
3. Centripetal Acceleration
Centripetal acceleration occurs when an object moves in a circular path at a constant speed. Even though the speed remains constant, the direction of the object’s velocity changes, which results in acceleration. Centripetal acceleration always points toward the center of the circular path, keeping the object in motion along the curved trajectory.
The formula for centripetal acceleration is:
ac=v2/r
Where:
- ac is centripetal acceleration,
- v is the tangential velocity of the object,
- r is the radius of the circular path.
Example:
Consider a car driving around a circular track at a constant speed of 20 m/s20 \, m/s. If the radius of the track is 5050 meters, the centripetal acceleration can be calculated as:
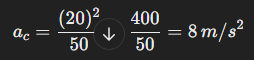
This means that, although the car’s speed remains constant, its direction is constantly changing, causing an acceleration directed toward the center of the circle with a magnitude of 8 m/s2.
Relation Between Acceleration, Velocity, and Time
To understand how acceleration affects an object’s motion, it is essential to consider the relationship between velocity (the rate of change of position) and time. Velocity and acceleration are closely related because acceleration describes how velocity changes with time.
- If the velocity of an object increases, it experiences positive acceleration.
- If the velocity of an object decreases, it experiences negative acceleration or deceleration.
- If an object’s velocity remains constant (no change in speed or direction), the acceleration is zero.
In situations where the initial velocity and acceleration of an object are known, we can predict the object’s velocity after a certain time has passed using the following formula:
v=u+at
Where:
- v is the final velocity,
- u is the initial velocity,
- a is the acceleration,
- t is the time.
Example of Accelerating Car:
Imagine a car traveling at an initial speed of 10 m/s, and it accelerates at a rate of 3 m/s2 for 4 seconds. To find the final velocity, we use the equation:
v=u+at=10+(3×4)=10+12=22 m/s
After 4 seconds, the car is traveling at a velocity of 22 m/s.
Acceleration Due to Gravity
One of the most common examples of uniform acceleration in physics is the acceleration due to gravity. On Earth, when an object is in free fall (assuming there is no air resistance), it accelerates toward the ground at a constant rate of approximately 9.8 m/s2. This value is known as gravitational acceleration and is denoted by g.
Objects in free fall experience a continuous increase in velocity as they descend. This means that for every second an object falls, its velocity increases by 9.8 m/s.
Example:
If a ball is dropped from a height and falls freely under the influence of gravity, its velocity after 3 seconds can be calculated using the equation:
v=u+gt
Since the ball starts from rest, u=0, so:
v=0+(9.8×3)=29.4 m/s
After 3 seconds, the ball will be traveling at a speed of 29.4 m/s.
The Concept of Deceleration
Deceleration is a type of acceleration where an object slows down, meaning its velocity decreases over time. Although deceleration is often referred to as “negative acceleration,” it still follows the same principles as regular acceleration but with the final velocity being less than the initial velocity.
Example:
A car traveling at 30 m/s begins to slow down as it approaches a stoplight. If the car decelerates at a rate of 5 m/s2, we can calculate how long it will take for the car to come to a complete stop using the following formula:
v=u+at
Rearranging for time (t):
t=v−ua
Since the final velocity v=0 (the car comes to a stop), the formula becomes:
t=0−30−5=−30−5=6 seconds
It will take the car 6 seconds to come to a complete stop.
Graphical Representation of Acceleration
Acceleration can also be represented graphically by plotting velocity against time. The slope of a velocity-time graph provides information about the acceleration of the object:
- If the graph shows a straight line sloping upward, the object has constant acceleration.
- If the graph shows a curved line, the object is experiencing non-uniform acceleration.
- If the graph has a horizontal line, this indicates that the object is moving at a constant velocity and the acceleration is zero.
Example:
Consider a velocity-time graph for an object accelerating uniformly from rest. The graph would show a straight line starting at the origin (0,0), indicating that velocity increases at a constant rate over time. The slope of this line represents the object’s acceleration.
Factors Affecting Acceleration
Several factors can influence the acceleration of an object:
- Force: According to Newton’s Second Law of Motion, the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. This is expressed in the formula:F=maWhere F is the force applied, mm is the mass, and aa is the acceleration. A greater force results in greater acceleration, while a larger mass results in smaller acceleration for the same amount of force.
Example: If two objects of different masses are subjected to the same force, the object with the smaller mass will experience a greater acceleration than the object with the larger mass.
- Friction and Air Resistance: Friction between an object and the surface it moves on, or air resistance acting against a moving object, can reduce acceleration. For example, a car moving on a rough road experiences more friction and thus requires more force to accelerate compared to a car moving on a smooth surface.
- Inclined Planes: The angle of an incline can affect an object’s acceleration due to gravity. An object sliding down a steeper slope will experience greater acceleration compared to an object on a more gradual slope.
Conclusion
Acceleration is a central concept in understanding motion and the forces that cause changes in velocity. Whether an object speeds up, slows down, or changes direction, acceleration plays a vital role in describing its motion. Understanding the relationship between acceleration, velocity, and time allows us to predict and describe various real-world phenomena, from a car accelerating on a highway to a ball falling freely due to gravity.
Through examples of uniform and non-uniform acceleration, as well as centripetal acceleration, it becomes clear how acceleration influences objects in motion. By applying the principles of acceleration to practical scenarios, we can better comprehend how the forces of nature govern the movement of objects, both large and small.