Algebra Symbols: Understanding Key Symbols and Their Uses in Mathematical Expressions

Algebra is a branch of mathematics that uses symbols to represent numbers, quantities, and operations in formulas and equations. These algebra symbols serve as a universal language, allowing mathematicians, scientists, and engineers to communicate complex ideas and solve problems effectively. Algebraic symbols include variables, operators, relational signs, grouping symbols, and constants, each with unique meanings and applications.

Whether you’re solving equations, working with functions, or exploring advanced mathematical concepts, understanding algebraic symbols is essential for interpreting and manipulating mathematical expressions. This article will explore some of the most important symbols in algebra, including variables, operators, and relational signs, and provide examples to illustrate how they are used in various mathematical contexts.

1. Variables and Constants

Variables and constants are fundamental symbols in algebra that represent quantities in mathematical expressions and equations.

Variables

In algebra, variables are symbols (usually letters) that represent unknown or changeable values. They allow mathematicians to work with general formulas and solve problems involving unknown quantities. The most common variables used in algebra are letters such as x, y, and z.

Example: In the equation 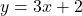$y = 3x + 2$ , x and y are variables. The value of 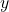$y$ depends on the value assigned to 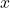$x$ , making both of them changeable within the equation.

Variables can take on different values depending on the problem, which is why they are especially useful in functions, inequalities, and equations. For example, in a real-world application, $x$ might represent the number of hours worked, while $y$ could represent total earnings.

Constants

Constants are fixed values that do not change within an equation or expression. Numbers like 2, 5, π (pi), or even letters assigned a specific value (like k for a rate constant) are examples of constants.

Example: In the formula for the circumference of a circle, $C = 2πr$ , π (approximately equal to 3.14159) is a constant that represents a fixed ratio in every circle.

Example: Using Variables and Constants in an Equation

Consider the equation $y = mx + c$ , which is the general form of a linear equation. Here:

m and c are constants that determine the slope and y-intercept of the line.
x and y are variables that represent points on the line.

In this equation, if $m = 2$ and $c = 3$ , then the equation becomes $y = 2x + 3$ , where x and y are the changing quantities.

2. Operators

Operators are symbols that denote specific mathematical operations, such as addition, subtraction, multiplication, division, and exponents. Understanding these operators is crucial for solving algebraic expressions and equations.

Basic Operators

1. Addition (+): The plus symbol denotes addition.
– Example: $x + 5$ represents adding 5 to the value of $x$ .

2. Subtraction (−): The minus symbol represents subtraction.
– Example: $y - 3$ means 3 is subtracted from $y$ .

3. Multiplication (× or ⋅): Multiplication can be represented by different symbols, but in algebra, a simple dot or no symbol at all is commonly used.
– Example: $4x$ means 4 multiplied by $x$ , while $3 \cdot z$ means 3 times $z$ .

4. Division (÷ or /): Division can be represented by the division sign or a slash.
– Example: $x / 2$ means $x$ divided by 2.

5. Exponentiation (^ or superscript): Exponents are used to represent repeated multiplication.
– Example: $x^2$ (or $x^3$ for cubing) means $x$ multiplied by itself twice, which is written as $x \cdot x$ .

Advanced Operators

1. Square Root (√): The square root symbol represents the value that, when multiplied by itself, gives the original number.
– Example: $\sqrt{16} = 4$ because $4 \times 4 = 16$ .

2. Absolute Value (| |): Absolute value represents the distance of a number from zero, regardless of direction.
– Example: $| -5 | = 5$ because the distance of -5 from 0 is 5.

3. Factorial (!): Factorial is used in permutations, combinations, and series, denoted by ! and applied to natural numbers.
– Example: $5! = 5 \times 4 \times 3 \times 2 \times 1 = 120$ .

Example: Combining Operators in an Expression

Consider the expression $3x^2 + 2x - 5$ .

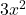The term $3x^2$ represents 3 times 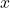$x$ squared.
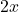$2x$ means 2 multiplied by $x$ .
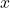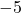$-5$ is a constant being subtracted.

This expression combines multiplication, exponentiation, and subtraction, demonstrating how operators work together in algebraic expressions.

3. Relational Symbols

Relational symbols represent the relationship between two quantities, which is essential for writing and solving equations and inequalities in algebra.

Basic Relational Symbols

1. Equals (=): The equals sign shows that two expressions are equal.
– Example: $3x + 2 = 8$ means that $3x + 2$ is equal to 8.

2. Greater Than (>): Indicates that the value on the left is greater than the value on the right.
– Example: $x > 5$ means $x$ is any value greater than 5.

3. Less Than (<): Indicates that the value on the left is less than the value on the right.
– Example: $y < 7$ means $y$ is any value less than 7.

4. Greater Than or Equal To (≥) and Less Than or Equal To (≤): Used to indicate that one side is greater than or equal to, or less than or equal to, the other side.
– Example: $x \geq 10$ means $x$ can be 10 or any value greater than 10.

Example: Using Relational Symbols in Inequalities

An inequality like $2x + 3 > 7$ means that we are looking for values of $x$ that make the expression $2x + 3$ greater than 7. By solving this inequality, we can find that:

$2x + 3 > 7$

Subtract 3 from both sides:

$2x > 4$

Divide by 2:

$x > 2$

This means that any value of $x$ greater than 2 will satisfy the inequality.

4. Grouping Symbols

Grouping symbols are used in algebra to indicate the order in which operations should be performed. The most common grouping symbols include parentheses ( ), brackets [ ], and braces { }. Grouping symbols follow the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction).

Types of Grouping Symbols

1. Parentheses ( ): Used to enclose parts of an expression that should be calculated first.
– Example: In $2 \times (3 + 4)$ , the expression inside the parentheses is calculated first, giving $2 \times 7 = 14$ .

2. Brackets [ ] and Braces { }: Used when there are multiple layers of grouping within an expression. They indicate that certain operations should be performed before others within a larger calculation.
– Example: In the expression $[(2 + 3) \times 4] - 5$ , the operation inside the parentheses is performed first, followed by multiplication, then subtraction.

Example: Complex Expression with Grouping Symbols

Consider the expression $(3 + 2) \times [5 - (1 + 2)]$ .

Calculate inside the innermost parentheses first: $(1 + 2) = 3$ .
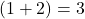Substitute back into the expression: $(3 + 2) \times [5 - 3]$ .
Then calculate inside the brackets: $5 - 3 = 2$ .
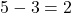Substitute back and multiply: $(3 + 2) \times 2 = 5 \times 2 = 10$ .

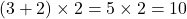Grouping symbols allow us to control the order of operations and achieve the correct answer.

5. Special Algebra Symbols

Several specialized symbols are unique to algebra and higher-level mathematics, including summation, product, and set notation symbols.

Summation (Σ)

The summation symbol (Σ) is used

to denote the sum of a sequence of terms, especially useful in series and functions. The formula below shows a general form of the summation:

$\sum_{i=1}^{n} a_i$

Where $a_i$ represents the terms in the sequence and $i$ is the index of summation that runs from 1 to $n$ .

Example: $\sum_{i=1}^{5} i = 1 + 2 + 3 + 4 + 5 = 15$ .

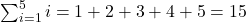Product (∏)

The product symbol (∏) represents the product of a sequence of terms, much like the summation symbol, but for multiplication rather than addition.

$\prod_{i=1}^{n} a_i$

This notation indicates the multiplication of each term $a_i$ as $i$ ranges from 1 to $n$ .

Example: $\prod_{i=1}^{4} i = 1 \times 2 \times 3 \times 4 = 24$ .

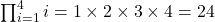Set Notation Symbols

Algebra frequently uses set notation to work with groups of numbers or solutions:
1. Union ( ∪ ): Represents the union of two sets, containing all elements from both sets.
– Example: If $A = \{1, 2, 3\}$ and $B = \{3, 4, 5\}$ , then $A \cup B = \{1, 2, 3, 4, 5\}$ .

2. Intersection ( ∩ ): Represents the common elements between two sets.
– Example: With the same sets $A$ and $B$ , $A \cap B = \{3\}$ .

Conclusion: The Role of Symbols in Algebra

Algebra symbols provide the foundation for building and solving mathematical expressions and equations. Understanding variables, operators, relational signs, grouping symbols, and special notations helps simplify and solve complex problems efficiently. These symbols not only convey specific instructions within mathematical expressions but also help represent abstract ideas, making algebra a versatile and powerful tool in both academic studies and practical applications.

With these symbols, algebra becomes a language through which we can explore, express, and understand patterns, relationships, and processes in mathematics and beyond. As we delve deeper into algebra, mastery of these symbols and their meanings will serve as a valuable asset for problem-solving and analytical thinking.