Ampere’s Law is one of the fundamental principles in electromagnetism, offering a profound insight into the relationship between electricity and magnetism. Named after André-Marie Ampère, a French physicist and mathematician, this law plays a crucial role in understanding how magnetic fields are generated by electric currents. Ampere’s Law forms part of Maxwell’s Equations, which are the cornerstone of classical electromagnetism, and it provides a powerful tool for calculating the magnetic fields created by currents in a variety of situations.

In this article, we will explore the conceptual foundations of Ampere’s Law, its mathematical formulation, and practical applications. Through examples, we will clarify how this law operates in real-world scenarios and demonstrate its significance in both theoretical and applied physics.
What Is Ampere’s Law?
Ampere’s Law relates the circulation of the magnetic field around a closed loop to the total current passing through the enclosed area. In simple terms, it provides a direct way to calculate the magnetic field generated by an electric current. It states that the integral of the magnetic field along a closed path is proportional to the total current that flows through the area enclosed by that path.
The mathematical expression for Ampere’s Law in its integral form is:
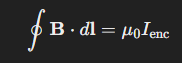
Where:
- B is the magnetic field,
- dl is an infinitesimal segment of the closed loop (path),
- μ0 is the permeability of free space (4π×10−7 T⋅m/A),
- IencI_{\text{enc}} is the net current passing through the enclosed loop.
Ampere’s Law essentially tells us that the magnetic field around a current-carrying wire is proportional to the current in the wire. By using this law, one can calculate the magnetic field around wires, loops, or coils, making it a powerful tool for solving electromagnetic problems.
Conceptual Foundations of Ampere’s Law
Ampere’s Law is rooted in the fundamental idea that moving electric charges create magnetic fields. This relationship between electricity and magnetism was first explored by Hans Christian Ørsted in 1820, when he discovered that a compass needle could be deflected by a nearby electric current. Ampère later formalized this relationship into a law that could quantify the magnetic field produced by a given current.
Magnetic Fields Generated by Current
The key idea behind Ampere’s Law is that electric currents generate magnetic fields. This magnetic field forms concentric loops around the wire carrying the current, with the direction of the field determined by the right-hand rule: if the thumb of your right hand points in the direction of the current, the curl of your fingers shows the direction of the magnetic field around the wire.
The strength of this magnetic field diminishes as you move farther from the wire, and the field lines form closed loops around the current. The concept of circulation in Ampere’s Law refers to summing up the magnetic field along a closed loop path around the current. The greater the current, the stronger the magnetic field will be, and Ampere’s Law quantitatively links the two.
Mathematical Formulation of Ampere’s Law
Ampere’s Law is most commonly written in its integral form, as shown above. This form of the law is particularly useful when dealing with symmetrical situations, such as long straight wires, solenoids, or toroids, where the magnetic field has a predictable pattern.
Let’s break down the components of the mathematical expression:
- ∮B⋅dl: This represents the line integral of the magnetic field B around a closed loop. The symbol ∮ indicates that the integration is performed around a closed path, and dl is a small segment of this loop. The dot product between B and dl ensures that only the component of the magnetic field that is tangent to the loop contributes to the integral.
- μ0: The permeability of free space is a constant that appears in Ampere’s Law and other equations in electromagnetism. It represents how much resistance free space offers to the formation of a magnetic field.
- Ienc: This is the total current enclosed by the path of integration. If there are multiple wires inside the loop, the net current is the algebraic sum of the currents, taking into account the direction of each current.
Ampere’s Law can also be expressed in a differential form using one of Maxwell’s Equations:
∇×B=μ0J
Where:
- ∇×B represents the curl of the magnetic field B\mathbf{B},
- J is the current density vector.
This form is used in situations where the current distribution is not as simple, and we need to calculate the magnetic field on a point-by-point basis.
Applications of Ampere’s Law
Ampere’s Law is widely used in electromagnetism, especially in situations where there is symmetry that simplifies the computation of the magnetic field. Below are some common applications of Ampere’s Law in real-world scenarios.
1. Magnetic Field Around a Long Straight Wire
One of the most straightforward applications of Ampere’s Law is in determining the magnetic field around a long, straight wire carrying a steady current. Using Ampere’s Law, we can calculate the magnetic field at a distance rr from the wire.
Consider a long, straight wire carrying a current II. We choose a circular path around the wire with radius rr, centered on the wire. Due to the cylindrical symmetry of the problem, the magnetic field B\mathbf{B} is constant in magnitude and always tangential to the path.
Applying Ampere’s Law:
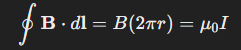
Thus, the magnetic field at a distance rr from the wire is:
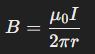
This equation shows that the magnetic field around a long straight wire decreases inversely with the distance from the wire.
Example: In power transmission lines, which carry high currents over long distances, Ampere’s Law helps calculate the magnetic fields generated around the wires. This is important for designing safety measures and ensuring that magnetic fields do not interfere with nearby electronic equipment.
2. Magnetic Field Inside a Solenoid
A solenoid is a coil of wire that generates a magnetic field when an electric current passes through it. Solenoids are used in many applications, such as electromagnets, motors, and inductors. Ampere’s Law can be applied to determine the magnetic field inside a solenoid.
Consider an ideal solenoid with nn turns per unit length, carrying a current I. Inside the solenoid, the magnetic field is uniform and parallel to the axis of the solenoid. Outside the solenoid, the field is negligible.
We can apply Ampere’s Law by choosing a rectangular path that runs parallel to the solenoid axis inside the coil and outside the coil. Since the magnetic field outside the solenoid is nearly zero, the contribution to the line integral comes only from the section inside the solenoid.
Using Ampere’s Law:
BL=μ0nIL
Where is the length of the path inside the solenoid. Simplifying, we find the magnetic field inside the solenoid:
B=μ0nI
This equation shows that the magnetic field inside a solenoid depends only on the current and the number of turns per unit length, and it is independent of the solenoid’s diameter or length.
Example: Electromagnets are commonly used in electric motors, relays, and MRI machines. The magnetic field inside these electromagnets can be calculated using Ampere’s Law to ensure they generate the correct field strength for their intended function.
3. Magnetic Field in a Toroid
A toroid is a doughnut-shaped coil used in applications like transformers and inductors. Ampere’s Law is particularly useful for calculating the magnetic field inside a toroid, which, due to its symmetry, confines the magnetic field to the space inside the coils.
Consider a toroid with N turns, carrying a current I, and with a radius rr from the center of the toroid to a point inside the coil. Ampere’s Law can be applied using a circular path inside the toroid. The magnetic field is tangential to this path, and applying the law gives:
B(2πr)=μ0NI
Solving for , the magnetic field inside the toroid is:
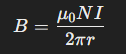
This shows that the magnetic field inside a toroid decreases as you move farther from the center, following an inverse relationship with the distance rr.
Example: Toroidal transformers are widely used in electrical systems, especially where efficient energy transfer is required with minimal magnetic field leakage. The ability to confine the magnetic field within the core of the toroid minimizes interference with other components.
Limitations of Ampere’s Law
While Ampere’s Law is a powerful tool, it has its limitations. In its simplest form, Ampere’s Law is only applicable in situations where there is sufficient symmetry to simplify the integral, such as in cases of infinite straight wires, solenoids, and toroids. In more complex scenarios, where the current distribution is irregular, or the geometry is more complicated, the use of Ampere’s Law requires more advanced techniques, such as the differential form combined with Maxwell’s Equations.
Additionally, Ampere’s Law, in its original form, does not account for the fact that time-varying electric fields can also produce magnetic fields. This limitation was addressed by James Clerk Maxwell, who introduced the concept of displacement current into Ampere’s Law, completing the set of equations that govern electromagnetism. The modified version of Ampere’s Law, which is one of Maxwell’s Equations, is written as:
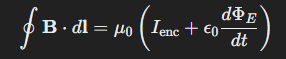
Where ϵ0 is the permittivity of free space and dΦE/dt is the rate of change of electric flux. This term accounts for the creation of magnetic fields by changing electric fields, a key concept in electromagnetic waves.
Conclusion
Ampere’s Law is a cornerstone of classical electromagnetism, linking electric currents to the magnetic fields they produce. Its mathematical formulation, particularly in the integral form, offers a powerful way to calculate magnetic fields in symmetrical situations such as around long straight wires, inside solenoids, and within toroids. Despite its limitations in certain cases, Ampere’s Law remains a fundamental tool in physics and engineering.
From the design of electric motors and transformers to the development of magnetic fields in scientific experiments, the applications of Ampere’s Law are vast and varied. As part of Maxwell’s Equations, it not only describes magnetic fields generated by currents but also contributes to our understanding of electromagnetic waves and the propagation of light. Ampere’s Law, thus, continues to play a critical role in both theoretical and applied physics, shaping the way we understand and utilize electromagnetism.