Applications of Trigonometry: Practical Uses and Real-World Examples

Trigonometry is a branch of mathematics that studies the relationships between the angles and sides of triangles. These relationships, defined by trigonometric functions like sine, cosine, and tangent, play a crucial role in solving problems involving angles, distances, and dimensions in both two- and three-dimensional space. Beyond academia, trigonometry has countless applications in various fields, from physics and engineering to navigation and architecture.

This article explores several key applications of trigonometry in real-world scenarios, illustrating how this mathematical tool aids in calculations and decision-making in complex situations.

Trigonometry in Architecture and Construction

In architecture and construction, trigonometry is essential for designing and building structures with precision. Architects and engineers use trigonometric functions to calculate angles, heights, lengths, and distances, ensuring that structures are safe, balanced, and meet specified dimensions.

1. Designing Angles and Dimensions in Buildings:

Example: Suppose an architect is designing a sloped roof with a specific angle of inclination for rainwater drainage. If the roof needs to slope at a 30° angle, and the horizontal base measures 20 feet, the architect can use trigonometry to calculate the required roof height. By applying the tangent function:

$\text{tan}(30^\circ) = \frac{\text{opposite (height)}}{\text{adjacent (base length)}}$

Rearranging, we find:

$\text{height} = 20 \times \text{tan}(30^\circ) \approx 20 \times 0.577 = 11.54 \text{ feet}$

This calculation ensures that the roof design meets the specifications, helping with material estimation and construction accuracy.

2. Ensuring Structural Stability:

Trigonometry helps engineers calculate loads and forces, especially in designs involving slopes or angled structures. For example, in constructing a bridge with angled support beams, trigonometry is used to determine the lengths and load-bearing capacities necessary to ensure the bridge’s stability.

Trigonometry in Physics and Engineering

Physics and engineering often involve motion, forces, and wave patterns, all of which can be analyzed using trigonometric principles. Trigonometry allows scientists and engineers to calculate distances, determine angles, and analyze wave behavior.

1. Projectile Motion:

When an object is launched at an angle, such as a cannonball or a basketball, trigonometry is used to determine its range, maximum height, and time of flight.
Example: Suppose a ball is thrown at a 45° angle with an initial velocity of 20 m/s. To find the horizontal and vertical components of this velocity, we use trigonometry:
Horizontal component ( $v_x$ ) = $20 \times \cos(45^\circ) \approx 20 \times 0.707 = 14.14 \, \text{m/s}$
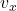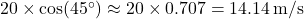
Vertical component ( $v_y$ ) = $20 \times \sin(45^\circ) \approx 20 \times 0.707 = 14.14 \, \text{m/s}$
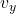With these components, we can calculate the maximum height and total distance traveled, allowing engineers and physicists to model real-world scenarios in projectile motion.

2. Electrical Engineering:

Trigonometry is crucial in analyzing alternating current (AC) circuits, which involve sinusoidal waveforms. The voltage and current in AC circuits vary over time in a sinusoidal manner, and trigonometric functions help in calculating the peak and RMS (Root Mean Square) values.
Example: In an AC circuit with a voltage peak of $V_0 = 120$ volts and a frequency of 50 Hz, the voltage at any point in time 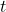$t$ can be expressed as:

$V(t) = V_0 \cdot \sin(2 \pi f t) = 120 \cdot \sin(2 \pi \cdot 50 \cdot t)$

This function allows engineers to predict voltage variations over time and ensure that electrical systems operate safely.

Trigonometry in Navigation and Cartography

Before modern GPS, sailors and navigators relied on trigonometry to calculate distances and determine positions on maps. Even today, trigonometric principles remain foundational in navigation and mapping, providing insights into distances, locations, and angles on the Earth’s surface.

1. Latitude and Longitude Calculations:

Example: Navigators use trigonometry to determine their position based on latitude and longitude. If a ship is located at a certain latitude and wants to calculate the distance to another point on the same longitude, they use the formula:

$\text{distance} = R \cdot \Delta \theta$

where R is the Earth’s radius (about 6,371 km) and $\Delta \theta$ is the angular distance between the two latitudes in radians.

This calculation provides an accurate measure of distance, helping navigators plot routes across vast oceans.

2. Celestial Navigation:

Trigonometry is also fundamental in celestial navigation, where navigators determine their location based on the positions of celestial bodies (such as the sun, moon, and stars).
Example: By measuring the angle between the horizon and a celestial body at a specific time, navigators can calculate their latitude using trigonometric tables, a method that has been used for centuries.

Trigonometry in Astronomy

Astronomy heavily relies on trigonometry to study celestial bodies’ distances, sizes, and positions in space. By analyzing the angles and distances between stars and planets, astronomers can determine distances that are otherwise impossible to measure directly.

1. Calculating Distances to Stars:

One method astronomers use to measure distances to nearby stars is parallax, which involves measuring the apparent shift in a star’s position relative to distant background stars as observed from different points in Earth’s orbit.
Example: If a star’s parallax angle is 0.1 arcseconds, the distance 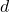$d$ in parsecs can be calculated as:

$d = \frac{1}{\text{parallax angle}} = \frac{1}{0.1} = 10 \, \text{parsecs}$

This trigonometric method allows astronomers to map our galaxy and understand the relative distances between celestial bodies.

2. Determining the Size of Celestial Bodies:

Trigonometry also helps astronomers calculate the size of planets, stars, and other objects. By measuring the angular diameter and knowing the distance, astronomers can determine the physical diameter.
Example: Suppose the moon has an angular diameter of 0.5° as seen from Earth, and the distance to the moon is 384,000 km. Using trigonometry:

$\text{Diameter} = 2 \times (\text{distance} \times \tan(\text{angular diameter} / 2))$

With this calculation, astronomers can determine the moon’s diameter, enhancing our understanding of its structure and composition.

Trigonometry in Music and Sound Engineering

Trigonometry is essential in analyzing and manipulating sound waves in music and audio engineering. Sound waves are sinusoidal, and their characteristics, such as frequency, wavelength, and amplitude, can be calculated and modified using trigonometric principles.

1. Sound Wave Analysis:

Sound engineers use trigonometric functions to model and analyze sound waves, allowing them to adjust audio properties, such as pitch and loudness.
Example: In a sound wave function 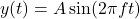$y(t) = A \sin(2 \pi f t)$ , where A is the amplitude and f is the frequency, trigonometry allows engineers to adjust these parameters to create different sound effects.

2. Harmonic Analysis in Music:

Trigonometry also helps in harmonic analysis, which involves breaking down complex sounds into simple sinusoidal components. This analysis is essential in music production to achieve clear, balanced sound quality.
Example: A musician might use harmonic analysis to combine multiple sound waves at different frequencies, creating harmony and texture in musical compositions.

Trigonometry in Medicine and Biology

In medicine and biology, trigonometry has applications in imaging techniques and anatomical studies. By measuring angles and distances, medical professionals and researchers can obtain accurate representations of the human body and biological structures.

1. Medical Imaging (CT and MRI Scans):

Trigonometry is used in CT (computed tomography) and MRI (magnetic resonance imaging) to create detailed images of internal organs and structures. By taking images from multiple angles and using trigonometric algorithms, these techniques generate 3D representations.
Example: In a CT scan, multiple 2D cross-sectional images are combined using trigonometric calculations, allowing doctors to observe detailed layers of the body and make accurate diagnoses.

2. Measuring Angles in Anatomy:

Trigonometry is essential for measuring anatomical angles, such as joint angles or the curvature of the spine.
Example: Orthopedic surgeons

may use trigonometry to calculate angles in the spine to assess and treat conditions like scoliosis. By measuring angles between vertebrae, doctors can determine the severity of curvature and plan appropriate treatments.

Trigonometry in Computer Graphics and Animation

Computer graphics and animation extensively use trigonometry to create realistic simulations and movements in virtual environments. Trigonometry helps animators and graphic designers model perspective, rotation, scaling, and lighting.

1. 3D Modeling and Rotation:

Trigonometric functions allow 3D objects to rotate and move realistically in virtual space.
Example: When designing a game, a developer may use trigonometry to calculate the angle at which a character turns, ensuring that movement appears smooth and natural on screen.

2. Rendering Light and Shadows:

In computer graphics, trigonometry is also crucial in rendering lighting and shadows accurately to create realistic images.
Example: By calculating the angle of light relative to an object, animators can apply shading techniques, creating depth and perspective that enhance the visual appeal of digital art.

Conclusion

Trigonometry’s applications extend far beyond theoretical mathematics. This mathematical field supports advancements in engineering, architecture, physics, medicine, and many other disciplines. By understanding and applying trigonometric functions like sine, cosine, and tangent, professionals can solve complex problems involving angles, distances, and dimensions, ultimately shaping our world in profound ways. As we continue to develop technology and explore new scientific fields, trigonometry will remain an indispensable tool in both practical and theoretical problem-solving.