Average velocity is a fundamental concept in physics that describes the rate at which an object changes its position over a certain time interval. Unlike speed, which only considers the distance traveled, average velocity is a vector quantity that includes both magnitude and direction. This makes average velocity particularly important in understanding motion, as it reflects the net effect of all directional changes and fluctuations in an object’s speed over a period of time.

In this article, we will explore the definition of average velocity, how it is calculated, its relation to speed, and practical examples to illustrate its significance in real-world contexts.
What is Average Velocity?
Average velocity is the displacement of an object divided by the time it takes to travel that displacement. Displacement, in this context, is the shortest straight-line distance between an object’s starting and ending points, along with a direction. Average velocity, therefore, tells us how fast and in what direction an object moves on average during a given time interval.
Formula for Average Velocity
The formula for calculating average velocity (![]() ) is:
) is:
![]()
where:
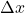 is the displacement, or the change in position of the object (final position
is the displacement, or the change in position of the object (final position 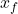 minus initial position
minus initial position 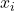 ),
),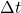 is the time interval over which the displacement occurs (final time
is the time interval over which the displacement occurs (final time 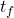 minus initial time
minus initial time 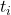 ).
).
Thus,
![]()
Since average velocity is a vector quantity, it has both magnitude and direction. The direction of average velocity is the same as the direction of the displacement vector.
Example of Average Velocity Calculation
Suppose a car travels 120 meters east over a period of 10 seconds. In this case:
- Displacement
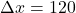 meters east.
meters east. - Time interval
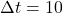 seconds.
seconds.
Using the formula:
![]()
Thus, the car’s average velocity is ![]() .
.
Difference Between Average Velocity and Average Speed
Average velocity and average speed are often confused, but they are different concepts. While average velocity considers displacement, average speed considers the total distance traveled, regardless of direction.
- Average Speed is defined as the total distance traveled divided by the total time taken, and it is a scalar quantity with only magnitude.
- Average Velocity is defined as displacement divided by time, and it includes both magnitude and direction, making it a vector quantity.
Example of Average Speed vs. Average Velocity
Imagine a person walks 50 meters north, then 50 meters south, taking a total of 20 seconds for the journey.
1. Total Distance Traveled: ![]()
2. Displacement: Since the person returns to the starting point, the displacement is 0 meters.
- Average Speed:
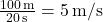
- Average Velocity:
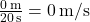
Thus, while the average speed is ![]() , the average velocity is
, the average velocity is ![]() , as there is no net displacement from the starting point.
, as there is no net displacement from the starting point.
Calculation of Average Velocity in Different Scenarios
The calculation of average velocity can vary depending on the type of motion. Let’s examine a few scenarios to understand how average velocity is determined in different contexts.
1. Straight-Line Motion
In straight-line motion, where an object moves in a single direction without reversing, the average velocity is simply the total displacement divided by the total time taken.
Example: A cyclist travels 200 meters north in 20 seconds.
- Displacement
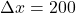 meters north.
meters north. - Time
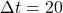 seconds.
seconds.
![]()
In this case, the average velocity is straightforward to calculate, as there is no change in direction.
2. Multi-Directional Motion
When an object moves in multiple directions, the displacement must be calculated as the vector sum of all the individual movements. Average velocity will depend on the net displacement rather than the total path length.
Example: A person walks 3 km east and then 4 km north in a total time of 1 hour.
1. Calculate Displacement: Since the person moves in a right-angle path, use the Pythagorean theorem to calculate the net displacement:
![]()
2. Calculate Average Velocity:
![]()
Thus, the person’s average velocity is 5 km/h in the northeast direction, even though the total distance walked was 7 km.
3. Circular Motion
In circular motion, if an object completes a full circle and returns to its starting point, its displacement is zero, resulting in an average velocity of zero.
Example: A runner completes one lap around a circular track with a circumference of 400 meters in 2 minutes.
1. Displacement: Since the runner ends at the starting point, the displacement is ![]() meters.
meters.
2. Average Velocity:
![]()
Despite covering a distance of 400 meters, the average velocity is zero because there is no net change in position.
Importance of Average Velocity in Real-Life Applications
Average velocity is useful in various real-life scenarios, particularly in physics, engineering, transportation, and navigation. Understanding average velocity allows us to analyze motion more accurately, predict travel times, and design efficient routes.
1. Transportation Planning
In transportation, average velocity is a critical factor for planning routes, predicting arrival times, and managing traffic. Knowing the average velocity helps in estimating the time required to cover specific distances and optimize route efficiency.
Example: A delivery driver travels 300 km over 5 hours to complete a delivery route, stopping occasionally. The average velocity of ![]() (assuming no return to the start) helps the company predict arrival times and schedule future deliveries.
(assuming no return to the start) helps the company predict arrival times and schedule future deliveries.
2. Sports Performance Analysis
Average velocity is often used in sports to assess athletes’ performance. Coaches use it to evaluate running speed, swimming velocity, and cycling performance, helping athletes set and achieve performance goals.
Example: A track runner completes a 400-meter race in 50 seconds. The average velocity is:
![]()
This average velocity can be used as a benchmark to track improvements over time or compare with other athletes’ performances.
3. Aviation and Navigation
In aviation and maritime navigation, average velocity is essential for plotting flight paths, estimating fuel usage, and determining the time required to reach destinations. By considering both speed and direction, navigators ensure that travel remains on course and efficient.
Example: An airplane flying at an average velocity of 500 km/h in a southwest direction for 2 hours covers an approximate displacement of 1000 km southwest. This information helps in coordinating with air traffic control and estimating arrival times.
Graphical Representation of Average Velocity
Average velocity can also be visualized on position-time graphs, where the slope of the line represents the object’s velocity. A constant slope indicates constant average velocity, while a changing slope indicates variable velocity.
Example of Position-Time Graph
Imagine an object moves from point ![]() meters at
meters at ![]() seconds to
seconds to ![]() meters at
meters at ![]() seconds. The position-time graph would be a straight line with a slope of:
seconds. The position-time graph would be a straight line with a slope of:
![]()
This slope, representing the change in position over time, is the average velocity of ![]() .
.
Key Differences Between Instantaneous and Average Velocity
- Average Velocity considers total displacement over total time, providing
an overview of motion over an interval.
- Instantaneous Velocity is the velocity at a specific point in time and can be obtained by finding the derivative of the position function with respect to time.
Average velocity gives a broad picture of overall movement, while instantaneous velocity captures precise motion at any given moment.
Conclusion
Average velocity is a crucial concept that enables us to understand motion in terms of displacement over time. As a vector quantity, it offers insights not just into the speed of movement, but also the direction, making it more comprehensive than average speed. Whether in analyzing transportation systems, evaluating sports performance, or navigating flight paths, average velocity provides essential data that helps in planning, analysis, and optimization. By understanding how average velocity is calculated and how it differs from speed, we gain a deeper appreciation of motion and its applications in real-world scenarios.