Avogadro’s Hypothesis: Definition, Explanation, and Applications

Avogadro’s Hypothesis, also known as Avogadro’s Law, is a fundamental principle in chemistry and molecular physics that states: *Equal volumes of gases, at the same temperature and pressure, contain an equal number of molecules.* This hypothesis provided the foundation for later developments in molecular theory and helped establish a clear understanding of the relationship between gas volume and the number of particles present.

First proposed by the Italian scientist Amedeo Avogadro in 1811, Avogadro’s Hypothesis was revolutionary for its time. Although initially not widely accepted, it eventually became one of the pillars of modern chemistry, leading to the calculation of Avogadro’s number, a constant representing the number of particles (atoms, ions, or molecules) in one mole of a substance.

In this article, we will explore Avogadro’s Hypothesis in detail, understand its implications for the study of gases, examine its relationship to the ideal gas law, and look at real-world applications and examples.

Understanding Avogadro’s Hypothesis

Avogadro’s Hypothesis asserts that, given the same temperature and pressure, equal volumes of different gases will contain the same number of molecules. This idea fundamentally means that gas volume depends on the number of molecules rather than the type of gas, provided temperature and pressure are constant.

Mathematically, Avogadro’s Hypothesis can be expressed as:

$V \propto n$

where:

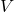$V$ is the volume of the gas,
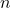$n$ is the number of moles (a measure of the number of molecules),
The proportionality sign ( 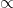$\propto$ ) indicates that volume is directly proportional to the number of moles when temperature and pressure are constant.

In other words, if the number of molecules (or moles) of gas doubles, the volume of the gas will also double, as long as temperature and pressure remain the same. This concept became critical in understanding the behavior of gases and allowed scientists to determine the molecular masses and formulas of compounds more accurately.

Example of Avogadro’s Hypothesis

Imagine two gas containers, one filled with hydrogen (H₂) and the other with oxygen (O₂), each having a volume of 1 liter, at the same temperature (e.g., 25°C) and pressure (e.g., 1 atm). According to Avogadro’s Hypothesis, both containers would contain the same number of molecules, despite the fact that hydrogen and oxygen have different molecular masses.

If each container contains one mole of gas, then each would have approximately $6.022 \times 10^{23}$ molecules (Avogadro’s number), regardless of the type of gas.

Relationship to the Ideal Gas Law

Avogadro’s Hypothesis played an essential role in the development of the ideal gas law, a formula used to describe the behavior of ideal gases. The ideal gas law is expressed as:

$PV = nRT$

where:

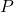$P$ is the pressure of the gas,
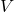$V$ is the volume of the gas,
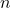$n$ is the number of moles,
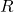$R$ is the ideal gas constant (approximately $8.314 \, \text{J/(mol·K)}$ ),
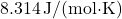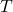$T$ is the temperature of the gas in Kelvin.

According to the ideal gas law, gas volume is directly proportional to the number of moles at constant temperature and pressure, which is precisely what Avogadro’s Hypothesis states. Avogadro’s contribution, therefore, became a foundational part of the ideal gas law, which links gas volume, pressure, and temperature to the number of gas particles.

Example Using the Ideal Gas Law

Suppose we have 2 moles of nitrogen gas (N₂) in a container at a temperature of 300 K and a pressure of 1 atm. We can use the ideal gas law to determine the volume $V$ :

$V = \frac{nRT}{P} = \frac{2 \times 8.314 \times 300}{1 \times 101.3} \approx 49.2 \, \text{L}$

If we double the number of moles (to 4 moles) while keeping temperature and pressure constant, the volume will also double, becoming approximately 98.4 L, demonstrating the direct proportionality between volume and moles.

Avogadro’s Number and the Mole Concept

Avogadro’s Hypothesis led to the determination of Avogadro’s Number, a key constant in chemistry that represents the number of particles in one mole of a substance. Avogadro’s Number is approximately:

$6.022 \times 10^{23} \, \text{particles per mole}$

This constant helps scientists calculate the number of atoms, ions, or molecules in a given sample of matter and is central to the concept of the mole. The mole allows chemists to count particles by measuring mass, enabling stoichiometric calculations in chemical reactions.

Practical Example Using Avogadro’s Number

Consider one mole of carbon dioxide gas (CO₂) at standard temperature and pressure (STP). Using Avogadro’s Number, we know that this sample contains approximately $6.022 \times 10^{23}$ molecules of CO₂. Avogadro’s Hypothesis tells us that if we have one mole of any gas (not just CO₂) at STP, it will occupy the same volume—approximately 22.4 liters—regardless of the type of gas.

Implications of Avogadro’s Hypothesis

Avogadro’s Hypothesis has several important implications for understanding gas behavior, molecular composition, and chemical reactions. It enables the comparison of gas volumes, calculations of molecular weights, and the derivation of balanced chemical equations.

1. Determining Molecular Formulas

Avogadro’s Hypothesis helped chemists establish molecular formulas by comparing the ratios of gas volumes. By observing how gases combine in fixed ratios of volume, scientists inferred the formulas of compounds, which was crucial in identifying the molecular structures of substances.

Example: Consider the formation of water from hydrogen and oxygen:

$2H_2 + O_2 \rightarrow 2H_2O$

This balanced equation shows that two volumes of hydrogen gas combine with one volume of oxygen gas to produce two volumes of water vapor. By using Avogadro’s Hypothesis, chemists could infer that water has the formula $H_2O$ rather than some other ratio.

2. Molar Volume of Gases

Avogadro’s Hypothesis led to the concept of molar volume, which is the volume occupied by one mole of gas at standard temperature and pressure (STP). At STP, any ideal gas occupies approximately 22.4 liters per mole. This uniformity allows for easy conversion between moles and volumes for gases, simplifying calculations in both laboratory and industrial settings.

Example: If we have 0.5 moles of nitrogen gas (N₂) at STP, we can use the molar volume to determine its volume:

$\text{Volume} = 0.5 \, \text{moles} \times 22.4 \, \text{L/mole} = 11.2 \, \text{L}$

Thus, at STP, 0.5 moles of nitrogen occupy 11.2 liters.

3. Gas Density Calculations

With Avogadro’s Hypothesis, we can calculate the density of gases based on their molar mass and molar volume at STP. Gas density is an essential parameter in industrial processes and environmental studies.

The density ( $\rho$ ) of a gas can be calculated as:

$\rho = \frac{\text{Molar Mass}}{\text{Molar Volume}}$

Example: To find the density of oxygen gas (O₂) at STP, we can use its molar mass (32 g/mol) and the molar volume (22.4 L/mol):

$\rho = \frac{32 \, \text{g/mol}}{22.4 \, \text{L/mol}} = 1.43 \, \text{g/L}$

Therefore, the density of oxygen gas at STP is approximately 1.43 g/L.

Applications of Avogadro’s Hypothesis in Real Life

Avogadro’s Hypothesis has practical applications across several fields, including chemistry, medicine, and engineering.

1. Chemical Reaction Calculations in Industry

Avogadro’s Hypothesis is crucial in industrial chemical reactions, where accurate measurements of gas quantities are essential for cost efficiency and product quality. Knowing that gases react in volume ratios allows industries to calculate the precise quantities of reactants and optimize production.

Example: In ammonia production using the Haber process, nitrogen and hydrogen react to form ammonia gas:

$N_2 + 3H_2 \rightarrow 2NH_3$

For every 1 volume of nitrogen, 3 volumes of hydrogen are required to produce 2 volumes of ammonia. Avogadro’s Hypothesis enables manufacturers to determine the exact volume of gases needed to maximize ammonia output.

2. Respiratory Medicine and Gas Exchange

In respiratory medicine, understanding the principles of gas volume and Avogadro’s Hypothesis aids in analyzing lung function and gas exchange. Oxygen and carbon dioxide are exchanged in the lungs in specific volumes, making gas volume calculations important for assessing respiratory health.

Example: Pulmonary function tests measure the volume of oxygen intake and carbon dioxide output. Knowing the volume of gas at body temperature and pressure helps doctors diagnose lung diseases and plan treatments accordingly.

3. Environmental

Science and Air Quality

In environmental science, Avogadro’s Hypothesis helps in measuring atmospheric gases and calculating pollution levels. Understanding gas volumes and the number of gas molecules in a given space allows researchers to assess air quality and track greenhouse gas emissions.

Example: Carbon dioxide concentrations are measured in parts per million (ppm) to monitor climate change. Avogadro’s Hypothesis helps scientists understand how CO₂ volumes relate to atmospheric pressure, temperature, and greenhouse effects.

4. Calculation of Atomic and Molecular Masses

Avogadro’s Hypothesis was instrumental in determining the atomic and molecular masses of elements and compounds. By comparing the volumes and densities of gases, scientists could infer the relative masses of atoms, leading to the development of atomic mass units and more precise chemical measurements.

Example: Using Avogadro’s Hypothesis, the relative mass of hydrogen was compared to oxygen, leading to the determination that oxygen is approximately 16 times heavier than hydrogen. This information was fundamental in establishing atomic weights for elements in the periodic table.

Conclusion

Avogadro’s Hypothesis, proposing that equal volumes of gases contain an equal number of molecules under the same conditions, revolutionized our understanding of matter and molecular structure. This hypothesis laid the groundwork for critical advancements in chemistry, including the ideal gas law, Avogadro’s number, and the mole concept. With real-world applications in industries like healthcare, environmental science, and chemical manufacturing, Avogadro’s Hypothesis continues to be relevant, underscoring the importance of molecular behavior in both theoretical and practical applications.

By allowing us to understand the relationship between gas volume and molecular quantity, Avogadro’s Hypothesis has provided a basis for calculating molar volumes, gas densities, and stoichiometric ratios in chemical reactions. These principles support our ability to measure, analyze, and optimize chemical processes on scales ranging from laboratory experiments to large-scale industrial production, making Avogadro’s contribution an enduring cornerstone of scientific knowledge.