In mathematics, a bijective function is a function that is both injective (one-to-one) and surjective (onto). Bijective functions establish a perfect pairing between elements in two sets, making them crucial in various fields, including algebra, calculus, and computer science. This unique property allows bijective functions to have inverses, which means each element in the output set (codomain) corresponds to precisely one element in the input set (domain), and vice versa. In this article, we will explore the concepts, properties, and applications of bijective functions, complete with examples to clarify each point.
Defining a Bijective Function
A function ![]() is bijective if it meets two specific criteria:
is bijective if it meets two specific criteria:
1. Injective (One-to-One): Each element of the domain ![]() maps to a unique element of the codomain
maps to a unique element of the codomain ![]() . In other words, if
. In other words, if ![]() , then
, then ![]() . There are no two different elements in
. There are no two different elements in ![]() that map to the same element in
that map to the same element in ![]() .
.
2. Surjective (Onto): Every element of the codomain ![]() is the image of at least one element in the domain
is the image of at least one element in the domain ![]() . This means that for every
. This means that for every ![]() , there exists an
, there exists an ![]() such that
such that ![]() .
.
When both conditions are satisfied, the function ![]() is bijective, ensuring that there is a one-to-one correspondence between elements in
is bijective, ensuring that there is a one-to-one correspondence between elements in ![]() and
and ![]() . Thus, each element in
. Thus, each element in ![]() has a unique “partner” in
has a unique “partner” in ![]() , and every element in
, and every element in ![]() is paired with an element in
is paired with an element in ![]() .
.
Visualizing Bijective Functions with Examples
Example 1: Bijective Function from Set 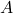 to Set
to Set 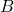
Consider two sets:
Define the function ![]() by the following mapping:
by the following mapping:
In this example:
- The function
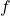 is injective because each element in
is injective because each element in 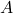 (1, 2, 3) maps to a unique element in
(1, 2, 3) maps to a unique element in 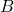 (a, b, c).
(a, b, c). - The function
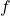 is also surjective because every element in
is also surjective because every element in 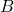 (a, b, c) is the image of an element in
(a, b, c) is the image of an element in 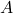 .
.
Since ![]() is both injective and surjective, it is bijective, meaning we can establish a perfect one-to-one correspondence between the elements of
is both injective and surjective, it is bijective, meaning we can establish a perfect one-to-one correspondence between the elements of ![]() and
and ![]() .
.
Example 2: Bijective Function in the Real Numbers
Consider the function ![]() (where
(where ![]() denotes the set of real numbers) defined by:
denotes the set of real numbers) defined by:
![]()
To determine if ![]() is bijective, let’s analyze injectivity and surjectivity:
is bijective, let’s analyze injectivity and surjectivity:
1. Injective: Suppose ![]() . Then:
. Then:
![]()
Subtracting 5 from both sides, we get ![]() . Thus,
. Thus, ![]() is injective because different inputs lead to different outputs.
is injective because different inputs lead to different outputs.
2. Surjective: For every ![]() , we need to find an
, we need to find an ![]() such that
such that ![]() . Solving for
. Solving for ![]() :
:
![]()
Since ![]() for any
for any ![]() , we conclude that
, we conclude that ![]() is surjective.
is surjective.
Since ![]() is both injective and surjective, it is a bijective function on
is both injective and surjective, it is a bijective function on ![]() . This function has an inverse,
. This function has an inverse, ![]() , demonstrating a one-to-one mapping between elements of
, demonstrating a one-to-one mapping between elements of ![]() to themselves.
to themselves.
Properties of Bijective Functions
Understanding the properties of bijective functions is essential, as they have unique characteristics that differentiate them from other types of functions.
1. Existence of an Inverse
A fundamental property of bijective functions is that they always have an inverse function. For a bijective function ![]() , there exists a function
, there exists a function ![]() such that:
such that:
![]()
This inverse function effectively “undoes” the mapping of ![]() , allowing us to move between the sets
, allowing us to move between the sets ![]() and
and ![]() in both directions.
in both directions.
Example: For the function ![]() , the inverse is
, the inverse is ![]() . This inverse function allows us to reverse the operation, showing that every
. This inverse function allows us to reverse the operation, showing that every ![]() in
in ![]() corresponds to exactly one
corresponds to exactly one ![]() in
in ![]() .
.
2. Composition of Bijective Functions
If two functions ![]() and
and ![]() are both bijective, their composition
are both bijective, their composition ![]() is also bijective. This is because the composition of injective (one-to-one) and surjective (onto) functions remains injective and surjective.
is also bijective. This is because the composition of injective (one-to-one) and surjective (onto) functions remains injective and surjective.
Example: Let ![]() and
and ![]() , where both functions are defined on the real numbers
, where both functions are defined on the real numbers ![]() . Since both
. Since both ![]() and
and ![]() are bijective, the composition
are bijective, the composition ![]() is also bijective.
is also bijective.
3. Cardinality of Sets
Bijective functions imply that the sets ![]() and
and ![]() have the same cardinality (i.e., they contain the same number of elements). This concept is essential in set theory and has applications in comparing the “sizes” of infinite sets.
have the same cardinality (i.e., they contain the same number of elements). This concept is essential in set theory and has applications in comparing the “sizes” of infinite sets.
Example: The function ![]() , mapping integers
, mapping integers ![]() to
to ![]() , is bijective. This bijection shows that there is a one-to-one correspondence between each integer and another integer, illustrating that the set of all integers has the same cardinality as itself.
, is bijective. This bijection shows that there is a one-to-one correspondence between each integer and another integer, illustrating that the set of all integers has the same cardinality as itself.
Applications of Bijective Functions
Bijective functions have significant applications across various fields due to their ability to create a one-to-one relationship between sets.
1. Cryptography
In cryptography, bijective functions are often used to encrypt and decrypt data. Each unique input (plain text) corresponds to a unique output (cipher text), and this relationship can be reversed with an inverse function, allowing secure communication.
Example: A simple encryption algorithm might add a fixed number to each character in a message. Since this transformation is bijective, it has a unique inverse, allowing the original message to be retrieved by reversing the transformation.
2. Calculus: Inverse Functions in Differentiation and Integration
In calculus, bijective functions play a role in finding inverse functions, which is useful in both differentiation and integration. If a function is bijective, we can find its inverse and apply differentiation or integration rules accordingly.
Example: The natural logarithm function ![]() is the inverse of the exponential function
is the inverse of the exponential function ![]() , which is bijective on the positive real numbers. This relationship is widely used in solving calculus problems involving exponential growth and decay.
, which is bijective on the positive real numbers. This relationship is widely used in solving calculus problems involving exponential growth and decay.
3. Computer Science: Hash Functions and Data Mapping
In computer science, hash functions often aim to create a one-to-one mapping between input data and hash codes. Bijective hash functions are ideal for applications where data retrieval speed is critical, as each input corresponds to a unique output.
Example: In a memory allocation system, a bijective hash function ensures that each memory address maps to a unique variable location, reducing the chance of data retrieval errors.
4. Set Theory: Establishing Cardinality of Infinite Sets
Bijective functions are essential in comparing the sizes of infinite sets. For instance, the set of all positive integers and the set of all integers have the same cardinality due to the existence of a bijective function between them.
Example: The function ![]() provides a bijective mapping between natural numbers
provides a bijective mapping between natural numbers ![]() and integers
and integers ![]() , showing that both sets have the same “size” despite being infinite.
, showing that both sets have the same “size” despite being infinite.
Conclusion
Bijective functions are a fundamental concept in mathematics, representing functions that map each element of one
set to a unique element in another set, with each element in the codomain having a corresponding element in the domain. Their injective and surjective properties allow bijective functions to have inverses, making them valuable in cryptography, calculus, computer science, and set theory. Through examples and applications, we see how bijective functions establish a precise one-to-one relationship between elements in different sets, enabling insights into the structure and relationships of mathematical objects. Whether you’re calculating inverse functions, encrypting data, or analyzing infinite sets, understanding bijective functions provides essential tools for exploring the connections between distinct mathematical entities.