Coordinate geometry, also known as analytic geometry or Cartesian geometry, is the branch of geometry that uses a coordinate system to define and manipulate the position of points, lines, and shapes. Unlike classical geometry, which relies on properties of shapes and relationships between angles and sides, coordinate geometry brings algebra and geometry together by using numbers and coordinates to explore geometric shapes and solve spatial problems.

By establishing a system with a horizontal axis (x-axis) and a vertical axis (y-axis), coordinate geometry provides a framework for analyzing relationships between points, distances, slopes, and areas, and it has applications in various fields, including physics, engineering, architecture, and navigation.
Basics of Coordinate Geometry
In coordinate geometry, each point is identified by an ordered pair ![]() that denotes its position relative to the origin
that denotes its position relative to the origin ![]() in the Cartesian plane. This system allows us to locate points, draw lines, and analyze geometric properties in a structured way.
in the Cartesian plane. This system allows us to locate points, draw lines, and analyze geometric properties in a structured way.
1. The Cartesian Plane:
- The Cartesian plane consists of two perpendicular axes: the x-axis (horizontal) and the y-axis (vertical). These axes intersect at the origin,
 .
. - The plane is divided into four quadrants:
- Quadrant I: Both
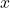 and
and 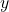 are positive
are positive 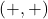 .
. - Quadrant II:
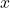 is negative and
is negative and 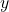 is positive
is positive 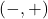 .
. - Quadrant III: Both
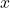 and
and 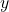 are negative
are negative  .
. - Quadrant IV:
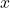 is positive and
is positive and 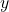 is negative
is negative  .
. - Example: The point
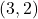 is located in Quadrant I, while the point
is located in Quadrant I, while the point 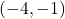 is in Quadrant III.
is in Quadrant III.
2. Coordinates of a Point:
- A point’s position is given by an ordered pair
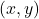 , where:
, where: - x represents the horizontal distance from the origin.
- y represents the vertical distance from the origin.
- Example: For the point
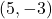 , 5 is the x-coordinate, indicating it is 5 units to the right of the origin, and -3 is the y-coordinate, indicating it is 3 units below the origin.
, 5 is the x-coordinate, indicating it is 5 units to the right of the origin, and -3 is the y-coordinate, indicating it is 3 units below the origin.
Distance Between Two Points
One of the foundational formulas in coordinate geometry is the distance formula, which calculates the distance between two points ![]() and
and ![]() on the plane. This formula is derived from the Pythagorean theorem and is expressed as:
on the plane. This formula is derived from the Pythagorean theorem and is expressed as:
![]()
Example:
- Problem: Find the distance between the points
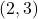 and
and 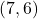 .
. - Solution:
- Using the formula:
![]()
- The distance between the points
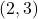 and
and 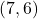 is approximately 5.83 units.
is approximately 5.83 units.
The Midpoint Formula
The midpoint formula is used to find the point that lies exactly halfway between two points ![]() and
and ![]() in the coordinate plane. The midpoint
in the coordinate plane. The midpoint ![]() is calculated by averaging the x-coordinates and y-coordinates of the two points:
is calculated by averaging the x-coordinates and y-coordinates of the two points:
![]()
Example:
- Problem: Find the midpoint between the points
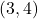 and
and 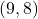 .
. - Solution:
- Using the formula:
![]()
- The midpoint between
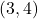 and
and 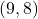 is
is 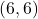 .
.
The Slope of a Line
The slope of a line measures its steepness and direction. It is calculated by finding the change in ![]() divided by the change in
divided by the change in ![]() (often called “rise over run”) between two points
(often called “rise over run”) between two points ![]() and
and ![]() on the line. The formula for slope
on the line. The formula for slope ![]() is:
is:
![]()
1. Positive Slope: The line rises as it moves from left to right.
2. Negative Slope: The line falls as it moves from left to right.
3. Zero Slope: The line is horizontal.
4. Undefined Slope: The line is vertical.
Example:
- Problem: Find the slope of the line passing through points
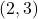 and
and 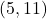 .
. - Solution:
- Using the formula:
![]()
- The slope of the line is
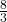 , indicating a positive, upward direction.
, indicating a positive, upward direction.
Equation of a Line
Coordinate geometry also provides various forms to represent the equation of a line, allowing us to describe any line on a plane.
1. Slope-Intercept Form:
- The slope-intercept form of a line’s equation is
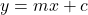 , where:
, where: 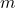 is the slope.
is the slope. is the y-intercept (the point where the line crosses the y-axis).
is the y-intercept (the point where the line crosses the y-axis).- Example: If the slope of a line is
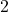 and the y-intercept is
and the y-intercept is 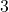 , then the equation of the line is:
, then the equation of the line is:
![]()
2. Point-Slope Form:
- If we know a point
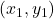 on the line and its slope
on the line and its slope 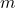 , we can use the point-slope form:
, we can use the point-slope form:
![]()
- Example: For a line passing through the point
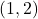 with a slope of
with a slope of 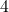 :
:
![]()
3. General Form:
- The general form of a line’s equation is written as
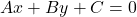 , where
, where 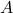 ,
, 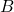 , and
, and  are constants.
are constants. - Example: The equation
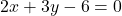 is in general form, representing a line on the Cartesian plane.
is in general form, representing a line on the Cartesian plane.
Circles in Coordinate Geometry
In coordinate geometry, circles are defined by their center and radius. The general equation of a circle with center ![]() and radius
and radius ![]() is:
is:
![]()
Example:
- Problem: Write the equation of a circle with center
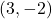 and radius
and radius 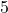 .
. - Solution:
- Substituting into the formula:
![]()
- This is the equation of the circle centered at
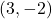 with a radius of 5 units.
with a radius of 5 units.
Applications of Coordinate Geometry in Real-World Scenarios
Coordinate geometry has countless applications in various fields, making it an invaluable tool for problem-solving.
1. Navigation and GPS:
- Coordinate geometry is foundational in navigation systems like GPS. By calculating distances and angles between latitude and longitude points, GPS systems accurately determine locations, distances, and routes.
- Example: GPS devices use coordinates to pinpoint your exact location and calculate the shortest or fastest route to a destination by measuring distances and directions between multiple points on the Earth’s surface.
2. Computer Graphics:
- In computer graphics, coordinate geometry is used to draw shapes, rotate objects, and design animations. The Cartesian plane enables designers to specify the position, scale, and orientation of objects.
- Example: In a video game, coordinate geometry determines the position of
characters and elements on the screen. Animators use transformations (translations, rotations, and scaling) based on coordinate calculations to create realistic movements.
3. Architecture and Design:
- Architects use coordinate geometry to create blueprints and designs, calculating distances, angles, and alignments between different elements to ensure precise dimensions and balanced structures.
- Example: In a building plan, architects use coordinates to position rooms, staircases, and windows accurately, ensuring that each element is located correctly on the construction site.
4. Robotics:
- Coordinate geometry aids in robotics by allowing precise positioning and movements within a defined space. Robots use coordinate systems to navigate environments, pick objects, and perform tasks with accuracy.
- Example: In a warehouse, robotic arms use coordinates to pick items from shelves based on specified x and y coordinates, increasing efficiency in inventory management.
5. Physics and Engineering:
- Physics relies on coordinate geometry to model the movement of objects, measure forces, and calculate distances. Engineers use it for designing structures, determining force distribution, and analyzing physical models.
- Example: In projectile motion analysis, the path of an object thrown at an angle is mapped on the Cartesian plane. Engineers calculate the object’s trajectory by considering its x and y coordinates over time.
Conclusion
Coordinate geometry bridges algebra and geometry, providing a framework for visualizing and solving spatial problems. With concepts like the distance formula, midpoint, slope, and equation of lines, coordinate geometry allows us to accurately define positions and relationships between points, lines, and shapes. Its applications extend to numerous fields, from navigation and computer graphics to architecture and physics, making it an essential tool in both theoretical and practical contexts. Through real-world examples, we see how coordinate geometry’s principles shape our understanding and manipulation of space, improving our ability to navigate, design, and innovate effectively.