Critical Velocity: Concept, Calculation, and Examples

Critical velocity is a fundamental concept in fluid dynamics and refers to the maximum velocity at which a fluid can flow through a pipe or channel without transitioning from laminar flow to turbulent flow. Understanding critical velocity is essential in fields such as engineering, physics, and environmental science, where the behavior of fluids plays a critical role in system design and performance. This article delves into the concept of critical velocity, the factors influencing it, the calculations involved, and real-world examples to illustrate its importance.

1. Understanding Critical Velocity

In fluid mechanics, critical velocity is defined as the velocity at which the flow pattern of a fluid changes from smooth and orderly (laminar flow) to chaotic and irregular (turbulent flow). This transition point is essential because the flow type significantly affects pressure, resistance, and the efficiency of fluid movement within a system.

Laminar vs. Turbulent Flow

Laminar Flow: In laminar flow, fluid particles move in parallel layers without any disruption between them. The flow is smooth, predictable, and has minimal friction. Laminar flow typically occurs at low velocities.
Turbulent Flow: In turbulent flow, fluid particles move in random directions, causing eddies and vortices. This chaotic movement increases resistance, pressure loss, and energy consumption, often leading to inefficiencies in fluid systems. Turbulent flow typically occurs at high velocities.

Critical Velocity is the threshold where flow switches from laminar to turbulent, and understanding this concept is essential for designing efficient fluid systems.

Factors Affecting Critical Velocity

Several factors influence critical velocity, including:

Viscosity of the Fluid: Fluids with higher viscosity (such as oils) tend to maintain laminar flow longer, meaning they have a higher critical velocity compared to low-viscosity fluids like water or air.
Density of the Fluid: The density of a fluid also affects how easily it transitions to turbulence. Generally, denser fluids can maintain laminar flow at higher velocities.
Diameter of the Pipe or Channel: In pipes or channels with larger diameters, the critical velocity is lower because there’s more space for particles to interact and cause turbulence.
Surface Roughness of the Pipe: Rougher surfaces in pipes or channels increase friction, encouraging the transition to turbulence even at lower velocities.

2. Mathematical Representation of Critical Velocity

The critical velocity ( $V_c$ ) can be determined using the Reynolds number, a dimensionless value that describes the relationship between inertial forces and viscous forces in fluid flow. The Reynolds number ( $Re$ ) for fluid flow in a pipe or channel is given by:

$Re = \frac{\rho V D}{\mu}$

where:

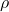$\rho$ is the density of the fluid,
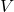$V$ is the velocity of the fluid,
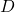$D$ is the diameter of the pipe or channel, and
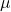$\mu$ is the dynamic viscosity of the fluid.

The critical Reynolds number for the transition from laminar to turbulent flow is typically around 2000 for flow in a pipe, although this threshold may vary slightly based on specific conditions. If the Reynolds number is below 2000, the flow is generally laminar; if it is above 2000, the flow becomes turbulent.

Calculating Critical Velocity Using Reynolds Number

The critical velocity $V_c$ can be isolated and calculated as follows:

$V_c = \frac{Re \cdot \mu}{\rho \cdot D}$

where $Re$ is set to 2000 (for most fluid flow cases) to represent the threshold for turbulence.

Example Calculation of Critical Velocity

Consider a scenario where water (with density $\rho = 1000 \, \text{kg/m}^3$ and dynamic viscosity $\mu = 0.001 \, \text{Pa} \cdot \text{s}$ ) flows through a pipe with a diameter of 0.05 m. To find the critical velocity at which the flow transitions from laminar to turbulent, set the Reynolds number to 2000:

1. Insert Values:

$V_c = \frac{2000 \times 0.001}{1000 \times 0.05}$

2. Simplify the Equation:

$V_c = \frac{2}{1000 \times 0.05} = \frac{2}{50} = 0.04 \, \text{m/s}$

Thus, the critical velocity for water flowing through this pipe is approximately 0.04 m/s. If the flow rate increases beyond this velocity, the flow will transition to turbulent.

3. Real-World Applications of Critical Velocity

The concept of critical velocity is essential in various fields, particularly in engineering, hydrodynamics, and environmental science. By understanding and controlling critical velocity, engineers can design systems that minimize friction, control flow rates, and maintain energy efficiency.

Application 1: Water Distribution Systems

In urban water distribution systems, engineers need to control the velocity of water flow to prevent turbulent flow, which can cause pipe damage, increase friction, and reduce efficiency. Knowing the critical velocity helps maintain laminar flow, reducing wear on pipes and ensuring consistent water pressure.

Example: For a municipal water system that supplies water through a large network of pipes, engineers calculate the critical velocity to prevent the flow from becoming turbulent, as turbulent flow can lead to high frictional losses and reduce water pressure at end-user points.

Application 2: Oil Pipelines

In oil pipelines, maintaining laminar flow is important for reducing energy costs. Since oil is a viscous fluid, it generally has a higher critical velocity compared to water. Engineers calculate critical velocity to ensure oil flows efficiently, minimizing energy consumption and wear within the pipeline system.

Example: In an offshore oil pipeline with a diameter of 1 meter, engineers calculate the critical velocity of crude oil. By adjusting the pump speed and pressure based on the viscosity and density of the oil, they keep the flow within the laminar range to optimize efficiency.

Application 3: Airflow in HVAC Systems

In heating, ventilation, and air conditioning (HVAC) systems, airflow within ducts needs to be carefully controlled. Excessively turbulent flow can lead to noise, increased resistance, and inefficient air distribution. Calculating the critical velocity of air ensures that the system operates quietly and efficiently.

Example: An HVAC engineer designs an air duct with a diameter of 0.2 meters. By calculating the critical velocity of air through the duct, the engineer can ensure that air flows smoothly, maintaining quiet operation without significant pressure loss.

Application 4: River and Stream Flow

In environmental science, understanding critical velocity is essential for studying rivers and streams. At certain flow velocities, a river can transition from smooth flow to turbulent flow, which can affect sediment transport, erosion rates, and the stability of riverbanks. Critical velocity calculations help in river management and flood prevention efforts.

Example: In a river with varying water depth and width, environmental scientists calculate critical velocity to determine the speed at which sediment will start to be displaced, affecting the river’s ecology and surrounding land stability.

4. Factors That Influence Critical Velocity

Several factors directly impact critical velocity, making it essential to consider these variables in practical applications:

Diameter of the Channel or Pipe: Larger pipes have lower critical velocities since the larger cross-section allows more space for turbulence to develop.
Fluid Properties: Both viscosity and density influence how quickly a fluid transitions to turbulence. More viscous fluids, like oil, tend to maintain laminar flow at higher velocities.
Surface Roughness: Rough surfaces within a pipe create disturbances in the flow, causing the transition to turbulence at lower velocities than if the surface were smooth.
Temperature: Temperature changes can affect a fluid’s viscosity and density, which in turn affect the critical velocity. For example, warmer water has lower viscosity than colder water, so the critical velocity will vary with temperature.

5. Importance of Critical Velocity in System Design and Maintenance

Critical velocity is a crucial factor in designing efficient and long-lasting systems. Below are some key considerations where critical velocity plays an important role:

Energy Efficiency

In applications where fluid flow is controlled, such as water supply systems or HVAC systems, knowing the critical velocity helps avoid turbulence. Turbulent flow increases friction, leading to higher energy consumption. By maintaining laminar flow, energy consumption can be minimized, resulting in more efficient system operation.

System Longevity

Excessive turbulence can cause wear and tear on pipes, valves, and other system components due to the increased friction and pressure variations associated with turbulent flow. By keeping fluid velocities below the critical threshold, engineers can extend the lifespan of these components, reducing maintenance costs and downtime.

Accurate Measurements

In fluid measurement devices, such as flowmeters, maintaining laminar flow is essential for accuracy. Turbulent flow can cause measurement errors and inconsistencies. Thus, critical velocity is a reference point to ensure that fluid flows steadily through these devices, providing accurate readings.

6. Example Calculations for Different Fluids

To illustrate the calculation of critical velocity for different fluids, let’s examine a few examples:

Example 1: Calculating Critical Velocity for Air in a Pipe

Suppose we have a pipe with a diameter of 0.1 meters carrying air with a density of $1.225 \, \text{kg/m}^3$ and a viscosity of $1. 81 \times 10^{-5} \, \text{Pa} \cdot \text{s}$ . Using the critical Reynolds number of 2000:

1. Insert values into the critical velocity formula:

$V_c = \frac{2000 \times 1.81 \times 10^{-5}}{1.225 \times 0.1}$

2. Simplify the equation:

$V_c = \frac{0.0362}{0.1225} \approx 0.296 \, \text{m/s}$

Thus, for air flowing through this pipe, the critical velocity is approximately 0.296 m/s.

Example 2: Calculating Critical Velocity for Oil in a Pipeline

For crude oil (density $\rho = 900 \, \text{kg/m}^3$ , viscosity $\mu = 0.1 \, \text{Pa} \cdot \text{s}$ ) flowing through a pipeline with a diameter of 0.5 meters:

1. Substitute into the formula:

$V_c = \frac{2000 \times 0.1}{900 \times 0.5}$

2. Simplify:

$V_c = \frac{200}{450} = 0.444 \, \text{m/s}$

The critical velocity for oil in this pipeline is approximately 0.444 m/s.

Conclusion

Critical velocity is a fundamental concept in fluid dynamics, defining the threshold between laminar and turbulent flow. This knowledge is vital for designing efficient systems across various fields, including engineering, environmental science, and industrial processing. Understanding critical velocity helps control energy consumption, reduce system wear, and maintain accurate fluid flow, ultimately contributing to safer, more effective fluid management systems. Through real-world applications and calculations, critical velocity demonstrates its value as a guiding principle in both theory and practical applications of fluid mechanics.