Derivation of Escape Velocity: Concept, Formula, and Applications

Escape velocity is the minimum speed an object must have to escape the gravitational pull of a celestial body, such as Earth, without any additional propulsion. Understanding escape velocity is fundamental in astrophysics, space exploration, and orbital mechanics, as it determines the speed needed for spacecraft or other objects to overcome gravity and enter space.

This article covers the concept of escape velocity, its derivation from basic physics principles, the formula used to calculate it, and its real-world applications.

Concept of Escape Velocity

Escape velocity is the minimum speed an object requires to overcome the gravitational force of a planet, star, or other celestial body and move away indefinitely without falling back. It depends on two main factors:
1. The mass of the celestial body.
2. The distance from the center of the celestial body to the point of departure.

An object traveling at escape velocity has enough kinetic energy to counterbalance the gravitational potential energy that holds it within the gravitational field. When it reaches escape velocity, the object’s kinetic energy becomes sufficient to offset the gravitational pull, allowing it to move infinitely far from the celestial body without requiring additional energy.

Key Characteristics of Escape Velocity

1. Independent of Mass of the Object: The escape velocity depends only on the gravitational field of the celestial body, not on the mass of the escaping object.
2. Direction Independent: Escape velocity is a scalar quantity, meaning it has magnitude but no specific direction.
3. Dependent on Distance and Mass of Celestial Body: Escape velocity varies with the mass and radius of the celestial body from which the object is escaping.

Example: On Earth, the escape velocity is approximately 11.2 km/s, meaning an object must travel at this speed (or higher) to leave Earth’s gravitational field without additional propulsion.

Derivation of the Escape Velocity Formula

The derivation of escape velocity involves equating the kinetic energy required to overcome gravitational potential energy. We assume that the object moves radially away from the celestial body, and we use Newton’s law of universal gravitation and the conservation of energy.

Step-by-Step Derivation

1. Gravitational Potential Energy

For an object of mass $m$ at a distance $r$ from the center of a celestial body with mass $M$ , the gravitational potential energy $U$ is given by:

$U = -\frac{GMm}{r}$

where:

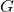$G$ is the gravitational constant ( $6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2$ ),
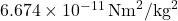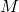$M$ is the mass of the celestial body,
$r$ is the distance from the center of the celestial body to the object.

The negative sign indicates that gravitational potential energy is a binding energy, and the object is bound within the gravitational field of the celestial body.

2. Kinetic Energy

To escape, the object needs to reach a point infinitely far away, where the gravitational potential energy becomes zero. The kinetic energy ( $K$ ) required for an object to achieve escape velocity $v_e$ is:

$K = \frac{1}{2}mv_e^2$

3. Conservation of Energy

For the object to escape, its total mechanical energy (kinetic energy plus gravitational potential energy) must be at least zero when it reaches an infinite distance. Initially, the total energy $E$ at the surface of the celestial body (distance $r = R$ ) is:

$E = K + U = \frac{1}{2}mv_e^2 - \frac{GMm}{R}$

For the object to escape, this total energy $E$ must be zero or greater. Thus,

$\frac{1}{2}mv_e^2 = \frac{GMm}{R}$

4. Solving for Escape Velocity

To find the escape velocity $v_e$ , we cancel the mass $m$ from both sides of the equation:

$\frac{1}{2}v_e^2 = \frac{GM}{R}$

Multiplying both sides by 2 gives:

$v_e^2 = \frac{2GM}{R}$

Taking the square root of both sides, we obtain the formula for escape velocity:

$v_e = \sqrt{\frac{2GM}{R}}$

where:

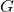$G$ is the gravitational constant,
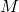$M$ is the mass of the celestial body,
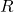$R$ is the radius of the celestial body (distance from the center to the surface).

Simplified Explanation of the Derivation

In simpler terms, escape velocity is derived by ensuring that an object’s initial kinetic energy is enough to counteract the gravitational potential energy binding it to the celestial body. If the kinetic energy equals the potential energy required to “climb out” of the gravitational field, the object will escape.

Example Calculation of Escape Velocity for Earth

Given:

Mass of Earth, $M = 5.972 \times 10^{24} \, \text{kg}$ ,
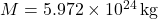Radius of Earth, $R = 6.371 \times 10^6 \, \text{m}$ ,
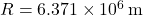Gravitational constant, $G = 6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2$ .

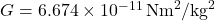Substituting these values into the formula:

$v_e = \sqrt{\frac{2 \times 6.674 \times 10^{-11} \times 5.972 \times 10^{24}}{6.371 \times 10^6}}$

$v_e = \sqrt{1.19 \times 10^8}$

$v_e \approx 11.2 \, \text{km/s}$

Thus, the escape velocity for Earth is approximately $11.2 \, \text{km/s}$ .

Factors Affecting Escape Velocity

The escape velocity depends on two main factors:

1. Mass of the Celestial Body (M): A larger mass creates a stronger gravitational pull, which increases the escape velocity. For instance, Jupiter, with a larger mass than Earth, has a higher escape velocity.
2. Radius of the Celestial Body (R): The escape velocity decreases with increasing radius, as the gravitational pull weakens with distance from the center of the celestial body.

Examples of Escape Velocities for Different Celestial Bodies

1. Moon: The Moon has a lower mass and a smaller radius than Earth, resulting in a lower escape velocity, around 2.38 km/s. This means an object requires much less speed to leave the Moon compared to Earth.
2. Jupiter: With its high mass, Jupiter has an escape velocity of about 59.5 km/s, making it much harder for objects to leave its gravitational field.
3. Sun: The Sun’s massive size gives it an escape velocity of around 617.5 km/s at its surface, illustrating the immense gravitational pull of large stars.

Applications of Escape Velocity

Escape velocity is a crucial concept in space exploration, orbital mechanics, and understanding celestial dynamics.

1. Spacecraft Launch

For spacecraft to leave Earth’s gravitational field and enter space, they must reach at least escape velocity (11.2 km/s for Earth). Rockets are designed with enough propulsion to provide this speed, allowing spacecraft to reach destinations beyond Earth’s orbit.

Example: The Apollo missions used powerful Saturn V rockets to launch astronauts and equipment toward the Moon, achieving escape velocity to break free from Earth’s gravitational influence.

2. Orbital Dynamics

While escape velocity is used to leave the gravitational field of a planet, it is also important in determining orbital characteristics. For instance, if a satellite’s speed is below escape velocity, it will remain in orbit around the Earth. By carefully adjusting speeds, engineers can place satellites in specific orbits or escape trajectories.

Example: Satellites in geostationary orbits travel at speeds just below escape velocity, balancing gravitational forces to maintain a stable orbit above a fixed point on Earth.

3. Planetary Atmospheres

Escape velocity also determines whether a celestial body can retain an atmosphere. Lighter molecules in a planet’s atmosphere may achieve speeds near escape velocity and gradually escape into space, especially if the planet’s escape velocity is low.

Example: The Moon, with its low escape velocity of 2.38 km/s, cannot hold a significant atmosphere, allowing gases to escape more easily than on Earth.

4. Astrobiology and Exoplanet Studies

Escape velocity is relevant in studying exoplanets and assessing whether they could retain atmospheres necessary for life. Planets with sufficient mass and radius have higher escape velocities, which can help them retain atmospheres despite solar winds or stellar radiation.

Example: Large exoplanets in the habitable zone of stars are more likely to have atmospheres that support life, as their high escape velocities help prevent atmospheric loss.

Energy Considerations in Escape Velocity

The concept of escape velocity involves balancing kinetic and potential energy:

Kinetic Energy: The energy an object has due to its motion, which must be sufficient to counter the gravitational pull.
Gravitational Potential Energy: The energy that binds the object to the celestial body, which must be overcome for the object to escape.

At escape velocity, the kinetic energy $\frac{1}{2}mv_e^2$ is exactly equal to the magnitude of the gravitational potential energy $\frac{GMm}{R}$ . This equality ensures that, at infinite distance,

the object’s total energy becomes zero, meaning it can travel away without further propulsion.

Limitations and Misconceptions About Escape Velocity

1. Not Required for Orbital Motion: Escape velocity is only necessary to leave a gravitational field completely. Satellites and other objects in orbit do not need to reach escape velocity, as they remain bound within Earth’s gravity.
2. Dependent on Starting Position: Escape velocity is calculated from the surface of the celestial body. If an object starts farther from the center, the escape velocity decreases.

Conclusion

The derivation of escape velocity provides essential insights into the physics of motion under gravity, helping us understand what it takes to break free from a celestial body’s gravitational influence. The escape velocity equation $v_e = \sqrt{\frac{2GM}{R}}$ illustrates how a combination of mass and radius influences this minimum required speed, and the concept has direct applications in space exploration, satellite deployment, and planetary science. Whether launching spacecraft, studying atmospheric retention, or understanding orbital mechanics, escape velocity is a foundational principle that allows scientists and engineers to design and execute successful space missions and explore the universe beyond our planet.