Doppler Effect Derivation and Explanation

The Doppler effect is a change in frequency or wavelength of a wave in relation to an observer who is moving relative to the source of the wave. This phenomenon is commonly experienced in sound and electromagnetic waves, such as sound from a moving vehicle or light from distant stars. Named after Austrian physicist Christian Doppler, the Doppler effect has significant applications in various fields, including astronomy, radar, medical imaging, and acoustics.

In this article, we’ll explore the derivation of the Doppler effect equations, discuss the principles behind it, and use practical examples to illustrate the concept.

Understanding the Basics of the Doppler Effect

The Doppler effect occurs because the relative motion between a source and an observer affects the observed frequency. When a sound source moves toward an observer, the waves compress, leading to a higher observed frequency, and when the source moves away, the waves stretch, leading to a lower observed frequency. The same principle applies to light waves, where a source moving toward the observer appears “blueshifted” (higher frequency), while a source moving away appears “redshifted” (lower frequency).

Derivation of the Doppler Effect for Sound Waves

We derive the Doppler effect formula by considering a source emitting sound waves of frequency $f_s$ (source frequency) and an observer who may be moving toward or away from the source. Sound waves travel through a medium (such as air) at a speed $v$ .

To derive the Doppler effect equations, let’s analyze two cases:
1. The Observer Moves While the Source is Stationary
2. The Source Moves While the Observer is Stationary

Case 1: The Observer Moves While the Source is Stationary

Let:

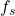$f_s$ be the frequency of the sound emitted by the source,
$v$ be the speed of sound in the medium (e.g., air),
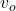$v_o$ be the speed of the observer relative to the source.

Derivation

1. The distance between wavefronts for sound waves emitted at frequency $f_s$ is the wavelength $\lambda$ of the sound:

$\lambda = \frac{v}{f_s}$

2. If the observer moves toward the source, they encounter wavefronts more frequently, effectively increasing the observed frequency $f_o$ . The speed of the observer relative to the speed of sound is $v + v_o$ , so the observed frequency is:

$f_o = \frac{v + v_o}{\lambda} = \frac{v + v_o}{\frac{v}{f_s}} = f_s \left( \frac{v + v_o}{v} \right)$

3. If the observer moves away from the source, the relative speed becomes $v - v_o$ , reducing the observed frequency:

$f_o = f_s \left( \frac{v - v_o}{v} \right)$

Summary Formula for Moving Observer (Source Stationary):

$f_o = f_s \left( \frac{v \pm v_o}{v} \right)$

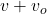Use $v + v_o$ when the observer moves toward the source.
Use 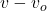$v - v_o$ when the observer moves away from the source.

Case 2: The Source Moves While the Observer is Stationary

Now, let:

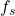$f_s$ be the frequency of the sound emitted by the source,
$v$ be the speed of sound in the medium,
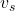$v_s$ be the speed of the source relative to the observer.

Derivation

1. When the source moves, it changes the effective wavelength of the waves reaching the observer, as the source’s motion either compresses or stretches the wavefronts.

2. If the source moves toward the observer, the effective wavelength $\lambda'$ decreases because each wavefront is closer to the previous one. The new wavelength becomes:

$\lambda' = \frac{v - v_s}{f_s}$

3. The observed frequency $f_o$ is then given by the speed of sound divided by this new wavelength:

$f_o = \frac{v}{\lambda'} = \frac{v}{\frac{v - v_s}{f_s}} = f_s \left( \frac{v}{v - v_s} \right)$

4. If the source moves away from the observer, the wavelength increases, and the frequency decreases:

$f_o = f_s \left( \frac{v}{v + v_s} \right)$

Summary Formula for Moving Source (Observer Stationary):

$f_o = f_s \left( \frac{v}{v \mp v_s} \right)$

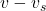Use $v - v_s$ when the source moves toward the observer.
Use 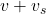$v + v_s$ when the source moves away from the observer.

General Doppler Effect Formula for Sound Waves

When both the source and observer are moving, we combine the two cases:

$f_o = f_s \frac{v \pm v_o}{v \mp v_s}$

The top signs are used when the observer and source move toward each other.
The bottom signs are used when the observer and source move away from each other.

Example Applications of the Doppler Effect in Sound

Example 1: Ambulance Siren Moving Toward and Away from a Stationary Observer

Suppose an ambulance with a siren emitting sound at a frequency $f_s = 500 \, \text{Hz}$ moves at $30 \, \text{m/s}$ , and the speed of sound in air is $340 \, \text{m/s}$ .

1. When the Ambulance Approaches the Observer:

$f_o = f_s \frac{v}{v - v_s} = 500 \frac{340}{340 - 30} = 500 \frac{340}{310} \approx 548.39 \, \text{Hz}$

The observer hears a higher frequency of approximately 548.39 Hz.

2. When the Ambulance Moves Away from the Observer:

$f_o = f_s \frac{v}{v + v_s} = 500 \frac{340}{340 + 30} = 500 \frac{340}{370} \approx 459.46 \, \text{Hz}$

The observer hears a lower frequency of approximately 459.46 Hz.

This explains why an ambulance siren sounds higher in pitch as it approaches and lower as it moves away.

Doppler Effect in Electromagnetic Waves (Light)

For light waves, the Doppler effect is used to understand phenomena such as redshift and blueshift in astronomy.

Blueshift occurs when a light source moves toward the observer, causing an increase in frequency and a shift toward the blue end of the spectrum.
Redshift occurs when the light source moves away, decreasing the frequency and shifting the light toward the red end of the spectrum.

The formula for the relativistic Doppler effect (considering the speed of light $c$ ) for light is:

$f_o = f_s \sqrt{\frac{1 + \frac{v}{c}}{1 - \frac{v}{c}}}$

where $v$ is the relative speed between the source and observer.

Example of Doppler Effect in Astronomy

Astronomers observe the light from distant galaxies to determine their movement. If a galaxy’s light is redshifted, it means the galaxy is moving away from us, which provides evidence of the universe’s expansion. For instance, if a galaxy has a redshift that corresponds to a speed of $30,000 \, \text{km/s}$ , astronomers can use the Doppler effect to calculate this movement and understand the galaxy’s behavior in the cosmic context.

Practical Uses of the Doppler Effect

Radar and Speed Detection: Police use Doppler radar to measure the speed of vehicles. When a radar signal is bounced off a moving car, the change in frequency of the reflected signal helps calculate the vehicle’s speed.
Medical Imaging: Doppler ultrasound is used to observe blood flow in medical diagnostics. The frequency shift of ultrasound waves reflected by moving blood cells helps measure blood flow speed and direction.
Weather Radar: Meteorologists use Doppler radar to track storms. Changes in radar signal frequency indicate the movement of raindrops and wind patterns, aiding in storm predictions.
Astronomy: Doppler shifts in starlight are used to detect exoplanets. When a star wobbles due to the gravitational pull of an orbiting planet, the observed frequency of its light changes, revealing information about the planet’s mass and orbit.

Summary

The Doppler effect explains how the relative motion between a source and observer alters the observed frequency of waves, whether sound or light. The derivation of Doppler effect formulas helps us quantify these changes, enabling applications in numerous fields like radar, medical imaging, and astronomy. Through practical examples, we see how the Doppler effect provides valuable insights into the movement and behavior of objects, both on Earth and in the cosmos.