Drift Velocity: Understanding the Motion of Electrons in a Conductor

Drift velocity is a fundamental concept in the study of electricity and electrical circuits, describing the average speed at which free electrons move through a conductor when an electric field is applied. This concept plays a critical role in understanding how electric current flows through wires and other conductive materials. While it may seem like electrons would move rapidly through a conductor given the speed of electrical signals, the reality is that the individual motion of electrons is much slower and follows a specific pattern known as drift velocity.

Drift velocity helps us explain the relationship between electric current, charge carriers (like electrons), and electric fields. It also provides insights into how different factors, such as the cross-sectional area of a conductor and the density of charge carriers, influence the flow of current. This article delves into the definition of drift velocity, the formula that describes it, and its practical applications, along with examples to help clarify the concept.

What Is Drift Velocity?

Drift velocity refers to the average velocity that free electrons attain in a conductor when subjected to an electric field. When a voltage is applied across a conductor, it creates an electric field inside the material. This field exerts a force on the free electrons, causing them to move. However, unlike a uniform and direct path, the electrons undergo a random motion due to collisions with the atoms of the conductor, which causes them to zigzag. Despite this random motion, when an electric field is applied, the electrons exhibit a net movement in a particular direction—toward the positive terminal of the voltage source. This net movement is what is described as the drift velocity.

Random Motion and Net Drift: Even without an electric field, electrons inside a conductor are constantly moving in random directions due to thermal energy. However, these random motions cancel each other out, resulting in no net flow of electrons or current. When an electric field is applied, it superimposes a net direction to this random movement, resulting in a slow drift of electrons in the direction opposite to the electric field (since electrons are negatively charged).
- Example: Imagine a conductor filled with billions of tiny particles, each bouncing around randomly. Now, if we tilt this conductor slightly, all particles will still bounce around but will gradually move in the direction of the tilt. Similarly, in a conductor, the electric field acts like the tilt, guiding the electrons toward a particular direction even as they continue their random motion.
Relation to Electric Current: Drift velocity is directly related to the concept of electric current. Current (I) is defined as the rate of flow of electric charge through a conductor, and drift velocity describes the speed at which these charges (electrons) move through the material.
- Example: In a copper wire carrying a current, the electrons move slowly with a certain drift velocity. However, the effects of the current are felt almost instantaneously across the circuit because the electric field propagates at the speed of light, causing electrons throughout the wire to begin moving nearly simultaneously.

Formula for Drift Velocity

The formula that relates drift velocity (vd) to the current (I) flowing through a conductor is given by:

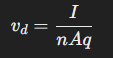
Where:

v_d = Drift velocity (m/s)
I = Electric current (A, amperes)
n = Number density of charge carriers (electrons) per unit volume (m³)
A = Cross-sectional area of the conductor (m2^2)
q = Charge of an electron (Coulombs), approximately 1.6×10⁻¹⁹ C

This formula shows how the drift velocity is influenced by the current, the physical properties of the conductor, and the charge of the carriers (electrons).

Understanding the Formula: The formula highlights that for a given current, the drift velocity is inversely proportional to the number density of charge carriers and the cross-sectional area of the conductor. This means that if a conductor has more free electrons per unit volume or a larger area, the electrons will drift more slowly for the same current.
- Example: Consider two wires made of different materials, such as copper and aluminum, with the same current passing through them. Since copper has a higher number density of free electrons than aluminum, the drift velocity of electrons in the copper wire will be slower compared to the drift velocity in the aluminum wire for the same current.
Drift Velocity and Current: From the formula, it is evident that if the current through a conductor increases, the drift velocity of electrons must also increase. This relationship allows engineers and scientists to calculate the behavior of electric currents in various materials.
- Example: In a household electrical circuit, increasing the current by turning on more appliances (like lights or a heater) causes a higher drift velocity of electrons in the wires. However, even with higher currents, the actual speed of electrons (drift velocity) remains relatively slow—typically on the order of millimeters per second.

Factors Affecting Drift Velocity

Several factors influence the drift velocity of electrons in a conductor. These include the strength of the applied electric field, the material properties of the conductor, temperature, and the cross-sectional area of the conductor.

Electric Field Strength: The strength of the electric field applied across a conductor affects the force acting on the free electrons, thus influencing their drift velocity. A stronger electric field results in a higher drift velocity as the force pushing the electrons becomes more significant.
- Example: In a simple battery-powered circuit, increasing the voltage of the battery increases the electric field in the circuit, leading to a higher drift velocity of the electrons. This means the electrons will move more quickly through the wire when a 9V battery is used compared to a 1.5V battery, even if the same wire is used.
Material of the Conductor: The type of material also affects the drift velocity due to differences in number density ( $n$ ) of free electrons. Conductors like copper and silver have a high density of free electrons, which allows them to carry current with lower drift velocity for a given current compared to materials like iron or aluminum.
- Example: Copper is often used in household wiring because it has a high number density of free electrons, allowing it to carry electric current efficiently with a relatively low drift velocity, reducing energy losses due to heat.
Temperature: As the temperature of a conductor increases, the thermal energy of the atoms in the conductor increases, causing more frequent collisions between electrons and atoms. This increased collision frequency tends to reduce drift velocity, even though the random thermal speed of electrons increases.
- Example: In power lines that carry current over long distances, heat can cause the wires to expand and reduce the drift velocity of electrons. This is why power lines are often designed with extra slack to accommodate thermal expansion during hot weather.
Cross-sectional Area: The larger the cross-sectional area of a conductor, the lower the drift velocity for a given current, because a larger area allows more electrons to move through the wire simultaneously.
- Example: In power cables that transmit electricity over long distances, cables with a larger cross-sectional area are used to ensure that the current flows smoothly with a lower drift velocity, which helps to minimize resistance and energy loss due to heating.

Practical Implications of Drift Velocity

Understanding drift velocity is crucial in designing and analyzing electrical systems, from small household circuits to large-scale power distribution networks. Drift velocity provides insights into the efficiency of current flow, energy losses, and the behavior of different materials as conductors.

Energy Losses in Conductors: Drift velocity plays a role in resistive heating, where the movement of electrons through a conductor generates heat due to collisions with atoms in the conductor. A higher drift velocity means more energy is transferred to the atoms, resulting in increased heat.
- Example: In electrical appliances like toasters or electric heaters, the heat generated is due to the resistive heating effect, which is a direct result of electrons moving with a certain drift velocity through the heating element.
Design of Electrical Components: Engineers use the concept of drift velocity to design wires and components that can handle specific amounts of current without overheating. For example, the thickness and material of the wire are chosen to ensure that the drift velocity remains within safe limits.
- Example: Electrical cables used in building wiring are designed to handle specific currents, with their cross-sectional areas calculated so that the drift velocity remains low, preventing the wires from becoming too hot and causing fire hazards.
Current Flow in Semiconductors: In semiconductors like silicon used in computer chips, the concept of drift velocity is essential for understanding how electrons and holes move under applied electric fields, affecting the performance of transistors and diodes.
- Example: In a solar cell, when sunlight generates electron-hole pairs in a semiconductor material, the drift velocity of these charge carriers determines how quickly the generated current can flow, affecting the efficiency of converting light into electrical energy.

Conclusion

Drift velocity is a key concept in understanding how electrical currents flow through conductors and the behavior of electrons under an electric field. Although individual electrons move slowly, the coordinated drift of billions of electrons results in the steady flow of electric current that powers our daily lives. By studying drift velocity, we gain insights into how materials behave as conductors, how current and resistance interact, and how electrical systems can be optimized for safety and efficiency. This concept remains fundamental in both theoretical and practical aspects of electrical engineering and physics, highlighting the complexity behind the seemingly simple flow of electricity.