Einstein’s Photoelectric Equation: Understanding the Quantum Nature of Light and the Photoelectric Effect

Einstein’s Photoelectric Equation revolutionized our understanding of light and energy, laying the groundwork for quantum mechanics. The equation describes the photoelectric effect, a phenomenon where light striking a metal surface causes the emission of electrons. Albert Einstein proposed that light consists of discrete packets of energy, known as photons, and explained that the energy of these photons must meet or exceed a specific threshold to dislodge electrons from a metal surface. His work earned him the Nobel Prize in Physics in 1921 and was instrumental in the development of quantum theory.

This article explores the fundamentals of Einstein’s Photoelectric Equation, its derivation, and the key concepts that make it significant in the field of physics, along with examples to illustrate its practical applications.

1. Understanding the Photoelectric Effect

The photoelectric effect occurs when electrons are emitted from a material, typically a metal, upon exposure to light. This effect was first observed by Heinrich Hertz in 1887 and further investigated by scientists like Wilhelm Hallwachs and Philipp Lenard. However, the phenomenon was puzzling because it could not be explained by classical wave theories of light.

Classical theory suggested that light’s energy depends on its intensity (brightness), so increasing light intensity should increase the energy of ejected electrons. However, experimental observations showed that:

Only light above a certain frequency (threshold frequency) could eject electrons, regardless of intensity.
Increasing light intensity increased the number of ejected electrons but not their energy.
Increasing the frequency of light increased the energy of the ejected electrons.

These observations contradicted classical theories and indicated that light behaves more like particles, with each particle carrying a specific energy dependent on its frequency.

2. Einstein’s Quantum Hypothesis and Photoelectric Equation

In 1905, Albert Einstein proposed a groundbreaking hypothesis to explain the photoelectric effect. He suggested that light is quantized and consists of discrete energy packets called photons. Each photon carries energy proportional to its frequency, as described by the equation:

$E = h \nu$

where:

E is the energy of the photon,
h is Planck’s constant (approximately 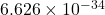$6.626 \times 10^{-34}$ J·s),
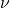$\nu$ is the frequency of the light.

Einstein’s hypothesis suggested that an electron would absorb energy from a single photon. If this energy exceeded a minimum amount required to overcome the work function of the material, the electron would be ejected from the surface.

3. Einstein’s Photoelectric Equation

Einstein’s Photoelectric Equation expresses the relationship between the energy of the incident photon, the work function of the material, and the kinetic energy of the emitted electron. The equation is:

$K_{\text{max}} = h \nu - \phi$

where:

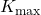$K_{\text{max}}$ is the maximum kinetic energy of the ejected electron,
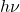$h \nu$ is the energy of the incident photon,
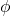$\phi$ is the work function of the material, the minimum energy required to eject an electron.

Key Concepts in the Photoelectric Equation

Photon Energy ( 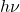$h \nu$ ): The energy of the incident photon depends directly on its frequency. Higher frequency light (such as UV light) carries more energy than lower frequency light (such as visible or infrared light).
Work Function ( 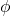$\phi$ ): The work function is a property of the material and represents the minimum energy required to remove an electron from the surface.
Kinetic Energy ( 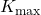$K_{\text{max}}$ ): If the photon’s energy exceeds the work function, the excess energy is converted into the kinetic energy of the ejected electron.

Example:

Consider light with a frequency of $8 \times 10^{14}$ Hz (which falls in the visible range) striking a metal with a work function of $4 \times 10^{-19}$ J.

1. Photon energy, $E = h \nu = (6.626 \times 10^{-34}) \times (8 \times 10^{14}) = 5.3 \times 10^{-19} \, \text{J}$ .
2. The kinetic energy of the emitted electron will be:

$K_{\text{max}} = h \nu - \phi = 5.3 \times 10^{-19} - 4 \times 10^{-19} = 1.3 \times 10^{-19} \, \text{J}$

If the photon energy is below $4 \times 10^{-19}$ J, no electrons will be emitted since the photon energy would be insufficient to overcome the metal’s work function.

4. Experimental Observations and Verifications of the Photoelectric Effect

The photoelectric effect exhibits characteristics that confirm the particle nature of light. These observations were experimentally verified and are consistent with Einstein’s equation.

a. Threshold Frequency

No electrons are ejected if the incident light frequency is below a certain threshold frequency, even if the light intensity is high. This threshold is directly related to the material’s work function, as the photon must have enough energy to overcome it.

Example:

For potassium, with a work function of about 2.3 eV, light with a frequency below the threshold of approximately $5.57 \times 10^{14}$ Hz (corresponding to a photon energy of 2.3 eV) will not eject electrons. Even if the light is intense, the lack of photon energy prevents electron emission.

b. Dependence on Light Frequency, Not Intensity

The kinetic energy of emitted electrons increases with the frequency of the incident light rather than its intensity. This is because frequency determines the photon energy, not the number of photons striking the surface.

Example:

If ultraviolet (UV) light (higher frequency) is shone on a metal surface, it will eject electrons with higher kinetic energy than red light (lower frequency), regardless of the red light’s intensity. Increasing intensity only increases the number of electrons emitted, not their kinetic energy.

5. Applications of Einstein’s Photoelectric Equation

Einstein’s Photoelectric Equation has wide-ranging applications across physics, engineering, and technology. Some of the most prominent applications include photovoltaic cells, photodetectors, electron microscopy, and understanding atomic and molecular structures.

a. Photovoltaic Cells (Solar Cells)

Photovoltaic cells convert light energy into electrical energy using the photoelectric effect. When sunlight (photons) strikes the solar cell, photons with sufficient energy dislodge electrons in the semiconductor material. The movement of these free electrons generates an electric current.

In solar cells, semiconductors like silicon are used with engineered work functions that match the energy of sunlight, maximizing the efficiency of electron ejection and, hence, energy production. By designing cells that operate efficiently under sunlight’s broad spectrum, solar panels harness a sustainable form of energy.

Example:

In a silicon-based solar cell, photons from sunlight provide enough energy to overcome silicon’s work function (about 1.1 eV). The resulting flow of ejected electrons creates an electric current, which is harnessed as solar power.

b. Photodetectors and Cameras

Photodetectors, which are widely used in cameras, night vision equipment, and optical sensors, rely on the photoelectric effect to detect light. When photons hit a photodetector material, they cause electrons to be emitted, generating a current proportional to the intensity of incoming light.

In digital cameras, a sensor (usually a CCD or CMOS) records light intensity and creates an image based on the photoelectric effect. Each pixel responds to the photons that hit it, ejecting electrons that convert into a measurable signal, creating a digital image.

Example:

In security systems, photodetectors help detect movement by identifying changes in light levels. When an intruder passes by, the change in light triggers a signal from the photodetector, alerting the system.

c. Electron Microscopy

Electron microscopes use the photoelectric effect to observe materials at atomic or molecular scales. These devices use high-energy photons to dislodge electrons from a material’s surface, producing images with high resolution.

Scanning Electron Microscopy (SEM) applies the photoelectric effect by focusing a beam of electrons onto a sample, causing electrons to be emitted. These secondary electrons are then detected to form an image of the sample with high spatial resolution, allowing scientists to study surface features at the nanoscale.

Example:

In nanotechnology and materials science, SEMs are used to observe structures and compositions of materials. The electron images provide critical insights into atomic structures, surface textures, and properties.

6. Impact of Einstein’s Photoelectric Equation on Quantum Theory

Einstein’s Photoelectric Equation was a milestone in the shift from classical to quantum mechanics. By proposing that light behaves as particles (photons) with quantized energy, Einstein challenged the classical wave theory of light and introduced the concept of wave-particle duality. This duality, which describes how light and other particles exhibit both wave-like and particle-like properties, became one of the foundations of quantum mechanics.

Planck-Einstein Relation and Quantum Mechanics

The equation $E = h \nu$ (photon energy) aligns with Max Planck’s hypothesis that energy is quantized. Planck introduced the idea of quantization to explain blackbody radiation, but Einstein extended it to light, further solidifying the idea that energy exists in discrete units. This quantization concept eventually led to the development of

quantum mechanics, a field that describes physical phenomena at the atomic and subatomic levels.

Conclusion

Einstein’s Photoelectric Equation provided an essential insight into the quantum nature of light, explaining the photoelectric effect and challenging classical concepts of wave behavior. By introducing the idea of photons and quantized energy, Einstein laid the groundwork for quantum mechanics and a new understanding of the interaction between light and matter. From the development of solar cells and photodetectors to the high-resolution images of electron microscopes, the applications of the photoelectric effect continue to impact technology and scientific research, proving Einstein’s work to be a cornerstone in both theoretical and applied physics.