Electron Spin: Definition, Quantum Mechanics, and Applications

Electron spin is a fundamental property of electrons and one of the key concepts in quantum mechanics. Spin describes the intrinsic angular momentum of an electron, representing a type of “rotation” that is unique to quantum particles. Unlike other forms of angular momentum, electron spin does not correspond to any physical spinning motion; instead, it is a quantum property that gives rise to magnetic behavior and has significant implications for atomic structure, chemical bonding, and modern technologies like magnetic resonance imaging (MRI) and quantum computing.

This article delves into the concept of electron spin, its role in quantum mechanics, the quantum numbers associated with it, and its applications in various fields.

What is Electron Spin?

Electron spin is a quantum property that represents the intrinsic angular momentum of an electron. In classical physics, angular momentum is associated with objects in rotational motion. However, electron spin is a purely quantum phenomenon with no classical counterpart, meaning it cannot be visualized as a particle physically spinning in space. Instead, it is a fundamental property of the electron that affects its magnetic moment and interactions with other particles.

Key Characteristics of Electron Spin

1. Quantization: Spin is quantized, meaning it can only take on certain discrete values. For electrons, the spin quantum number $s$ is fixed at $\frac{1}{2}$ .
2. Two Possible Orientations: Electrons can have two spin states, commonly labeled as “spin-up” and “spin-down.” These states correspond to the magnetic quantum number, $m_s$ , which can take values of $+\frac{1}{2}$ (spin-up) or $-\frac{1}{2}$ (spin-down).
3. Intrinsic Angular Momentum: Electron spin contributes to the overall angular momentum of the electron, affecting its behavior in electric and magnetic fields.
4. Magnetic Moment: Due to spin, electrons generate a magnetic moment, which causes them to interact with magnetic fields, creating effects like paramagnetism and diamagnetism in materials.

Example of Spin States

Consider an electron in a hydrogen atom. The electron can have a spin of either $+\frac{1}{2}$ or $-\frac{1}{2}$ , indicating whether the electron is in a spin-up or spin-down state. These two states influence the electron’s energy levels and how it interacts with magnetic fields. In a magnetic field, an electron with spin-up may align with the field, while an electron with spin-down may align oppositely, resulting in different magnetic energy states.

Quantum Mechanics and Electron Spin

Electron spin is an intrinsic quantum property, and understanding it requires quantum mechanics. The concept of spin is fundamental to quantum theory and is closely associated with several quantum mechanical principles, such as the Pauli exclusion principle, spin quantum numbers, and spin operators.

Quantum Numbers and Spin

Quantum numbers describe the quantized properties of electrons in an atom, including their energy levels, angular momentum, and spin.

1. Spin Quantum Number ( $s$ ): For an electron, the spin quantum number is always $\frac{1}{2}$ , a characteristic of all fermions, a class of particles to which electrons belong. This property differentiates fermions from bosons, which have integer spins.

2. Magnetic Spin Quantum Number ( $m_s$ ): The magnetic spin quantum number $m_s$ describes the orientation of the electron’s spin and can take values of $+\frac{1}{2}$ or $-\frac{1}{2}$ . These two orientations correspond to the spin-up and spin-down states of the electron.

3. Pauli Exclusion Principle: Proposed by Wolfgang Pauli in 1925, the Pauli exclusion principle states that no two electrons in an atom can have the same set of quantum numbers. As a result, two electrons occupying the same orbital must have opposite spins (one spin-up and one spin-down). This principle is fundamental to the structure of atoms and explains the arrangement of electrons in shells and subshells.

The Spin-½ System

Electrons are classified as spin-½ particles, meaning that their spin quantum number $s = \frac{1}{2}$ . This characteristic gives rise to only two possible spin states, $+\frac{1}{2}$ and $-\frac{1}{2}$ . Unlike classical angular momentum, which can vary continuously, quantum angular momentum is quantized, and for a spin-½ particle, it always has a fixed magnitude of $\sqrt{\frac{3}{4}} \, \hbar$ , where $\hbar$ is the reduced Planck constant.

Example of Electron Configuration and Spin

In an oxygen atom, which has eight electrons, the electron configuration is $1s^2 2s^2 2p^4$ . According to the Pauli exclusion principle, each orbital can hold only two electrons with opposite spins. In the 2p subshell, two of the p orbitals are fully occupied with paired electrons (one spin-up and one spin-down in each), while the third p orbital contains one unpaired electron. This unpaired electron gives oxygen its paramagnetic property, allowing it to be attracted to a magnetic field.

Magnetic Properties of Electron Spin

Electron spin gives rise to a magnetic moment, meaning that each electron behaves like a tiny magnet. When electrons are arranged in atoms, molecules, or materials, their spins can interact with external magnetic fields, leading to various magnetic properties such as paramagnetism, diamagnetism, and ferromagnetism.

1. Magnetic Moment and Spin

The magnetic moment ( $\mu$ ) of an electron is directly proportional to its spin. The magnetic moment associated with the electron’s spin is called the “spin magnetic moment” and is given by:

$\mu = g \cdot \frac{e}{2m} \cdot s$

where:

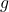$g$ is the electron’s g-factor (approximately 2.0023),
$e$ is the elementary charge,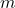
$m$ is the electron’s mass,
$s$ is the spin quantum number ( $\frac{1}{2}$ ).

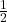2. Magnetic Properties of Materials

Diamagnetism: Diamagnetic materials contain paired electrons with opposite spins, canceling out each other’s magnetic moments. As a result, these materials exhibit weak repulsion in magnetic fields. Water and copper are examples of diamagnetic materials.
Paramagnetism: Paramagnetic materials have unpaired electrons, each contributing a net magnetic moment. These materials are attracted to external magnetic fields due to their unpaired electron spins. Examples include oxygen and aluminum.
Ferromagnetism: In ferromagnetic materials, such as iron, cobalt, and nickel, electron spins align parallel to each other in regions called “domains.” This alignment causes the material to exhibit strong magnetic properties even in the absence of an external field.

Example of Paramagnetism: Oxygen ( $\text{O}_2$ ) is paramagnetic because it has unpaired electrons in its molecular orbitals. When placed in a magnetic field, oxygen aligns its unpaired electron spins with the field, resulting in attraction to the magnetic field.

Spin and the Stern-Gerlach Experiment

The Stern-Gerlach experiment, conducted in 1922 by Otto Stern and Walther Gerlach, provided experimental evidence for the quantization of electron spin. In this experiment, a beam of silver atoms was passed through a magnetic field. Classical physics predicted that the beam would spread out into a continuous distribution; however, the beam split into two distinct paths, indicating that the magnetic moment of the electrons had discrete orientations (spin-up and spin-down).

This experiment was crucial in confirming the existence of quantized spin states and laid the groundwork for modern quantum mechanics.

Example of the Stern-Gerlach Experiment’s Results

In the Stern-Gerlach experiment, silver atoms were used because they have a single unpaired electron in their outermost shell. As the beam of silver atoms passed through a magnetic field, it split into two distinct parts, corresponding to spin-up and spin-down states. This experiment demonstrated that electron spin is quantized and can take only two orientations, which became a cornerstone of quantum theory.

Applications of Electron Spin

Electron spin has numerous applications in fields ranging from material science to medical imaging and quantum computing. Understanding and manipulating electron spin enables advancements in these areas.

1. Magnetic Resonance Imaging (MRI)

MRI is a medical imaging technique based on the principles of nuclear magnetic resonance (NMR). In MRI, the spin properties of hydrogen nuclei (protons) in the body are exploited to create detailed images of tissues. When placed in a magnetic field, the protons align according to their spin states. By applying radiofrequency pulses, the MRI machine alters these spin states, and the relaxation of spins back to their original alignment produces signals that are used to generate images.

Example: MRI scans are widely used in medicine to diagnose soft tissue injuries, neurological conditions, and tumors, providing clear, non-invasive images of internal body structures.

2. Electron Spin Resonance (ESR) or Electron Paramagnetic Resonance (EPR)

ESR is a technique used to study materials with unpaired electrons, such as free radicals and transition metals. When a sample with unpaired electrons is exposed to a magnetic field and radiofrequency energy, the electrons transition between spin states, emitting signals that reveal information about the sample’s structure and composition.

Example: ESR is used in chemistry and biology to study free radicals and reaction mechanisms. It is also used in materials science to analyze defects in solids and identify paramagnetic centers.

3. Spintronics

Spintronics (spin-based electronics) is an emerging field that exploits electron spin, in addition to charge, to store and process information. Traditional electronics rely solely on electron charge, while spintronics uses both the charge and spin, potentially allowing for faster, more efficient devices.

Example: Spintronic devices, such as magnetic random-access memory (MRAM), use electron spins to store data, leading to faster data access and lower energy consumption than traditional memory devices.

4. Quantum Computing

Quantum computing utilizes quantum bits, or qubits, which can exist in multiple states simultaneously, thanks to quantum properties like superposition and entanglement. Electron spin is one of the properties used to represent qubits. By manipulating electron spin states, researchers are developing quantum computers that can solve complex problems more efficiently than classical computers.

Example: A single electron’s spin states (spin-up and spin-down) can act as a qubit in quantum computing. Quantum computers are being developed to use such qubits to perform calculations at unprecedented speeds, promising advancements in fields like cryptography and optimization.

The Role of Electron Spin in Atomic and Molecular Structure

Electron spin plays a crucial role in the structure of atoms and molecules by influencing the way electrons occupy orbitals and form bonds. The arrangement of electron spins within atoms determines an element’s chemical behavior and reactivity.

Paired and Unpaired Electrons

1. Paired Electrons: Electrons with opposite spins occupy the same orbital, canceling each other’s magnetic moment. Atoms with only paired electrons are generally less reactive.

2. Unpaired Electrons: Atoms with unpaired electrons have net magnetic moments, making them more reactive and often paramagnetic.

Spin and Chemical Bonding

Electron spin also affects bonding behavior. For example, in covalent bonds, electrons with opposite spins pair up between atoms, creating stable bonds. In molecules with multiple unpaired electrons, interactions between spins can lead to different bonding arrangements, affecting molecular structure and magnetic properties.

Example: In the oxygen molecule ( $\text{O}_2$ ), the presence of unpaired electrons gives it paramagnetic properties, whereas nitrogen ( $\text{N}_2$ ), with all electrons paired, is diamagnetic.

Conclusion

Electron spin is a fundamental quantum property with no classical equivalent, representing an intrinsic angular momentum that influences an electron’s behavior in magnetic fields. As one of the defining characteristics of quantum mechanics, spin explains phenomena ranging from atomic structure and chemical bonding to advanced technologies like MRI, spintronics, and quantum computing. The quantized nature of electron spin has opened new frontiers in both science and technology, allowing for the development of devices that leverage the unique properties of quantum mechanics to advance knowledge and improve everyday applications. The study of electron spin continues to drive innovation, providing insights that bridge fundamental physics with real-world applications.