Empirical probability is a type of probability that is calculated based on the observation of outcomes from an experiment or a real-world process, rather than theoretical assumptions. It provides an estimate of the likelihood of an event occurring, determined by the frequency of the event happening relative to the total number of trials. Empirical probability is also known as experimental probability because it relies on actual experimental data or historical observations to make predictions about future events.

This method of determining probability is particularly useful when it is difficult or impossible to calculate theoretical probabilities, or when we want to use real-world data to inform decisions or make predictions. In this article, we will explore the concept of empirical probability, the steps for calculating it, and examples of its applications in various fields such as sports, business, and science.
What is Empirical Probability?
In probability theory, empirical probability is defined as the ratio of the number of times an event occurs to the total number of trials or observations. It is a way of estimating the likelihood of an event based on how often that event has occurred in the past. Unlike theoretical probability, which is based on known models or assumptions, empirical probability depends on actual results and experimental data.
The formula for calculating empirical probability is:
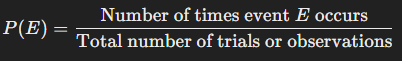
Where:
- P(E) represents the empirical probability of event E.
- The numerator is the number of times event E occurs in a set of trials or observations.
- The denominator is the total number of trials or observations.
Empirical probability gives us a practical way to estimate probabilities when we have access to data but not to the precise underlying probabilities of the events.
Example of Empirical Probability:
Suppose a basketball player takes 100 free throws, and she makes 72 of them. The empirical probability that she will make a free throw, based on past performance, is:
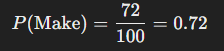
This means there is a 72% chance, based on past data, that the player will make a free throw. Notice that this estimate is based on observation, not theoretical calculation.
How to Calculate Empirical Probability
The process of calculating empirical probability involves a few straightforward steps. These steps allow us to estimate the likelihood of an event based on experimental or historical data.
Step 1: Collect Data
To calculate empirical probability, we first need a set of data from experiments or observations. This could be anything from recording how often a coin lands heads up to tracking customer purchases in a store. The larger the sample size or number of trials, the more accurate the empirical probability will be, as larger datasets reduce the impact of random fluctuations.
Step 2: Count the Occurrences of the Event
Once the data is collected, count the number of times the specific event of interest occurs. For instance, if you are observing how often a certain customer buys a product, you would count how many times that customer has made a purchase over a given period.
Step 3: Determine the Total Number of Trials
Next, determine the total number of trials or observations. This is the denominator in the empirical probability formula. For example, if you are observing the outcomes of a dice roll, the total number of trials would be the number of times the dice is rolled.
Step 4: Calculate the Probability
Finally, divide the number of times the event occurs by the total number of trials to find the empirical probability. The result will give you an estimate of the likelihood of that event based on past data.
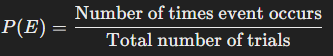
Example: Rolling a Die
Let’s say you roll a fair six-sided die 60 times and record how often the die lands on a 4. After 60 rolls, you find that the die landed on a 4 a total of 12 times. The empirical probability of rolling a 4 is:
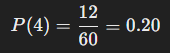
So, based on this experiment, the probability of rolling a 4 is 20%, even though the theoretical probability (since each side of a fair die should have an equal chance) is 16≈0.167\frac{1}{6} \approx 0.167. The empirical probability may differ from the theoretical probability due to the limited sample size, but as the number of trials increases, the empirical probability will tend to approach the theoretical probability.
Empirical vs. Theoretical Probability
While empirical probability is based on actual data from experiments or historical records, theoretical probability is based on known mathematical principles, assumptions, or models. Theoretical probability is calculated when we know all the possible outcomes and assume that each outcome has an equal likelihood of occurring.
Example of Theoretical Probability:
If you flip a fair coin, the theoretical probability of landing heads is:
![]()
This result is based on the assumption that both heads and tails are equally likely outcomes. However, empirical probability would be calculated by observing actual coin flips. If you flipped the coin 100 times and observed 47 heads, the empirical probability would be:
![]()
In this case, the empirical probability differs slightly from the theoretical probability due to natural variation in a small number of trials.
As the number of trials increases, empirical probability tends to converge toward theoretical probability, a principle known as the law of large numbers. This law states that as an experiment is repeated more times, the empirical probability becomes a more accurate estimate of the true probability.
Applications of Empirical Probability
Empirical probability is widely used in various fields, from predicting sports outcomes to understanding market behavior. It is especially useful in situations where theoretical probabilities are difficult to calculate or where real-world data offers a better estimate of outcomes.
1. Sports and Performance Analysis
Empirical probability plays a crucial role in sports, where it helps athletes, coaches, and analysts assess performance and predict future outcomes. By analyzing historical data, such as the number of successful goals, baskets, or passes, teams can make data-driven decisions to improve their strategies.
Example:
In baseball, a batter’s batting average is an empirical probability calculated by dividing the number of hits by the number of times the player has been at bat. If a player has 150 hits out of 500 at-bats, their batting average is:
![]()
This means the player has a 30% chance of getting a hit based on their past performance. Coaches and managers use this probability to make strategic decisions about player lineups and game plans.
2. Business and Market Analysis
In business, empirical probability is used to predict customer behavior, sales trends, and market demand. Companies collect data on past transactions, customer preferences, and product performance to estimate the likelihood of future events and to make informed business decisions.
Example:
A retail store wants to estimate the probability that a customer who enters the store will make a purchase. After observing 1,000 customers over a month, they find that 350 customers made purchases. The empirical probability that a customer will make a purchase is:
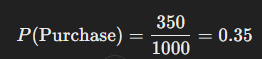
This probability can help the store adjust its inventory, staffing, and marketing efforts to maximize sales.
3. Weather Forecasting
Meteorologists rely on empirical probability to make accurate weather predictions. They collect historical weather data and use it to estimate the probability of various weather events, such as rain, snow, or storms, on a particular day.
Example:
If over the past 10 years it has rained on 200 out of 3650 days in a particular city, the empirical probability of rain on any given day is:

This means there is a 5.5% chance of rain based on historical weather patterns. Meteorologists use such probabilities to inform the public about potential weather conditions.
4. Medical Research
In medical research, empirical probability is used to understand the likelihood of various health outcomes or the effectiveness of treatments. By analyzing past patient data, researchers can estimate the probability of success or failure of a particular treatment or procedure.
Example:
A clinical trial involves 500 patients taking a new medication. If 425 patients respond positively to the treatment, the empirical probability of success for the treatment is:
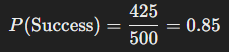
This means there is an 85% chance that the treatment will be successful based on the trial data, providing valuable information for doctors and healthcare providers.
5. Gambling and Gaming
Empirical probability is also applied in gambling and gaming industries to assess the odds of winning. Casino operators and gamblers use historical data to estimate the likelihood of various outcomes in games such as poker, blackjack, or roulette.
Example:
In a roulette game, suppose that after 500 spins, the number 17 has come up 12 times. The empirical probability of the ball landing on 17 in the next spin is:
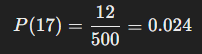
While this may differ from the theoretical probability (which is 1/37≈0.027 in European roulette), empirical probabilities provide insights into patterns that may help players make decisions.
Limitations of Empirical Probability
While empirical probability is a valuable tool, it has certain limitations:
- Limited by sample size: Small datasets can produce inaccurate estimates of probability. The larger the number of trials, the more reliable the empirical probability becomes.
- Subject to variation: Empirical probability can fluctuate based on randomness and the specific set of observations used, especially in small samples.
- Not always predictive: Even though empirical probability is based on past data, it may not always predict future outcomes accurately, particularly if the underlying conditions change.
Conclusion
Empirical probability is a powerful tool for estimating the likelihood of events based on real-world data and past observations. It is widely used in fields ranging from sports and business to weather forecasting and medical research. By analyzing historical outcomes, empirical probability helps us make informed decisions, optimize strategies, and predict future events with greater accuracy.
Although empirical probability may differ from theoretical probability, particularly with small sample sizes, it provides a practical approach to understanding the likelihood of events in real-world situations. As data becomes increasingly important in decision-making, empirical probability continues to play a critical role in improving predictions and refining strategies across industries and disciplines.