Energy Stored in a Capacitor: Theory, Formula, and Applications

A capacitor is an electrical component that stores and releases energy in the form of an electric field. It consists of two conductive plates separated by an insulating material, called the dielectric. When voltage is applied across the plates, an electric field develops, allowing the capacitor to store energy that can be released when needed. Capacitors play a crucial role in modern electronics, from stabilizing power supplies to filtering signals and providing quick bursts of energy. Understanding the energy stored in a capacitor, how to calculate it, and its practical applications is fundamental in fields such as electrical engineering, electronics, and renewable energy.

This article explores the theory behind energy storage in a capacitor, the mathematical formulas for calculating stored energy, and examples of how capacitors are used to store and manage energy in various applications.

How Capacitors Store Energy

Capacitors store energy in the form of an electric field created by the separation of electric charges on the plates. When a capacitor is connected to a voltage source, positive charges accumulate on one plate, while negative charges accumulate on the other. This separation of charges generates an electric field across the plates, with the dielectric material preventing current from flowing directly between them. The stored energy is directly related to the amount of charge, the applied voltage, and the capacitance of the capacitor.

Capacitance and the Role of the Dielectric

The amount of energy a capacitor can store depends on its capacitance, which is a measure of the capacitor’s ability to store charge. Capacitance, denoted by $C$ , is defined as:

$C = \frac{Q}{V}$

where:

$C$ is the capacitance in farads (F),
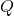$Q$ is the charge in coulombs (C) stored on the plates,
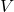$V$ is the voltage across the capacitor in volts (V).

The capacitance depends on factors such as the surface area of the plates, the distance between them, and the properties of the dielectric material. The dielectric serves as an insulator, allowing the plates to maintain a charge difference without direct current flow, which is crucial for energy storage. Dielectrics with a high dielectric constant allow capacitors to store more charge for the same voltage, increasing the energy storage capacity.

Electric Field and Energy Storage

The energy stored in a capacitor is directly related to the work required to separate the charges and create the electric field. When the capacitor is charged, an electric field forms between the plates, and the energy is stored within this field. The amount of stored energy is proportional to both the capacitance and the square of the voltage across the plates.

Formula for Energy Stored in a Capacitor

The energy $U$ stored in a capacitor can be derived from the relationship between voltage, charge, and capacitance. The formula for the energy stored in a capacitor is given by:

$U = \frac{1}{2} C V^2$

where:

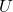$U$ is the energy stored in joules (J),
$C$ is the capacitance in farads (F),
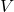$V$ is the voltage across the capacitor in volts (V).

This formula shows that the energy stored in a capacitor is proportional to the square of the voltage and directly proportional to the capacitance. Increasing either the voltage or the capacitance increases the amount of energy that can be stored.

Derivation of the Energy Formula

The energy stored in a capacitor can be derived by calculating the work done to move charge against the electric field between the plates. As the capacitor charges, the amount of work required to move an additional small charge $dq$ against the voltage $V$ across the capacitor is given by:

$dW = V \, dq$

Since $V = \frac{q}{C}$ , we can substitute and rewrite the expression as:

$dW = \frac{q}{C} \, dq$

To find the total work $W$ , we integrate this expression from 0 to $Q$ (the total charge):

$W = \int_0^Q \frac{q}{C} \, dq = \frac{1}{C} \int_0^Q q \, dq$

Solving the integral:

$W = \frac{1}{C} \left[ \frac{q^2}{2} \right]_0^Q = \frac{Q^2}{2C}$

Since $Q = CV$ , we can substitute $Q = CV$ to obtain the energy in terms of capacitance and voltage:

$U = \frac{1}{2} C V^2$

This formula is the standard equation for calculating the energy stored in a capacitor.

Examples of Energy Stored in a Capacitor

Understanding the energy storage capacity of capacitors is crucial in many applications, from power supply stabilization to flash photography. Here are some examples illustrating how the energy stored in a capacitor can be calculated and used.

Example 1: Calculating Energy in a Simple Capacitor Circuit

Consider a capacitor with a capacitance of $100 \, \mu F$ (microfarads) connected to a 10 V power source. To calculate the energy stored in the capacitor, we can use the formula:

$U = \frac{1}{2} C V^2$

Substituting the values:

$U = \frac{1}{2} \times 100 \times 10^{-6} \, \text{F} \times (10 \, \text{V})^2$

$U = \frac{1}{2} \times 100 \times 10^{-6} \times 100$

$U = 0.005 \, \text{J} = 5 \, \text{mJ}$

Thus, the energy stored in this capacitor is 5 millijoules (mJ).

Example 2: Energy Storage in a Camera Flash

Many camera flashes use capacitors to store energy and release it quickly to create a flash of light. Suppose a camera flash capacitor has a capacitance of $500 \, \mu F$ and is charged to a voltage of 300 V. The energy stored in the capacitor is calculated as follows:

$U = \frac{1}{2} C V^2$

Substituting the values:

$U = \frac{1}{2} \times 500 \times 10^{-6} \, \text{F} \times (300 \, \text{V})^2$

$U = \frac{1}{2} \times 500 \times 10^{-6} \times 90000$

$U = 22.5 \, \text{J}$

Therefore, the capacitor stores 22.5 joules of energy, which can be released quickly to produce a bright flash of light.

Example 3: Power Backup in Electronics

In some electronic circuits, capacitors are used as short-term power backups to prevent data loss during brief power interruptions. If a capacitor with a capacitance of 0.1 F is charged to 5 V, the energy stored can be calculated as:

$U = \frac{1}{2} C V^2$

Substituting the values:

$U = \frac{1}{2} \times 0.1 \, \text{F} \times (5 \, \text{V})^2$

$U = \frac{1}{2} \times 0.1 \times 25$

$U = 1.25 \, \text{J}$

This 1.25 joules of stored energy can provide power to critical components in the event of a brief power failure.

Applications of Energy Storage in Capacitors

Capacitors are widely used in electronics and electrical systems for their ability to store and release energy. Here are some of the key applications where the energy stored in capacitors is crucial:

1. Power Conditioning and Filtering

Capacitors are commonly used in power conditioning to filter out fluctuations in power supplies. In AC circuits, capacitors can smooth voltage spikes and noise, ensuring that sensitive components receive stable power. In DC circuits, capacitors work with inductors to stabilize power and prevent sudden voltage changes that could damage components.

Example: In power supplies, capacitors act as filters, storing and releasing energy to maintain a steady voltage. This is particularly important for devices such as computers, where even small voltage fluctuations can cause data errors.

2. Energy Storage for Rapid Discharge Applications

Capacitors are ideal for applications requiring a rapid discharge of energy. For example, camera flashes, defibrillators, and laser equipment often rely on capacitors to deliver quick bursts of high energy. Unlike batteries, which release energy slowly, capacitors can discharge their stored energy almost instantly.

Example: In defibrillators, capacitors store energy from a power source and release it quickly to deliver an electric shock to a patient’s heart, helping to restore a normal heartbeat.

3. Electric Vehicles and Regenerative Braking

In electric vehicles, capacitors are used for energy storage in regenerative braking systems. When a vehicle brakes, kinetic energy is converted

into electrical energy, which is stored in capacitors. This stored energy can then be used to power the vehicle, increasing its energy efficiency and reducing wear on the braking system.

Example: In hybrid and electric vehicles, supercapacitors store energy recovered from braking and release it during acceleration, providing an additional power boost and improving fuel efficiency.

4. Power Backup and Uninterruptible Power Supplies (UPS)

Capacitors are used in UPS systems as short-term energy storage devices, providing backup power during brief power outages. When the main power supply fails, the energy stored in capacitors can keep critical systems, such as medical equipment or computer servers, running until a generator or secondary power source takes over.

Example: In a data center, capacitors provide power backup to servers during a power outage, preventing data loss and allowing enough time for a generator to start.

5. Signal Processing and Timing Circuits

Capacitors play a crucial role in timing and signal-processing circuits. In oscillators and signal filters, capacitors store and release energy at specific intervals, helping to control the timing of electronic signals and filter out unwanted noise.

Example: In radio receivers, capacitors are used in tuning circuits to filter out specific frequencies, allowing the receiver to isolate and process the desired radio signal.

Relationship Between Energy Storage and Capacitance

The energy stored in a capacitor is proportional to both its capacitance and the square of the voltage. This relationship has significant implications for capacitor design and selection in different applications:

1. Increasing Capacitance: For applications requiring more energy storage, capacitors with higher capacitance values are used. Large capacitors, such as supercapacitors, can store significantly more energy and are useful in applications like regenerative braking and power backup systems.

2. Increasing Voltage: In situations where capacitance cannot be increased further, increasing the applied voltage can also increase the stored energy. However, capacitors have a maximum voltage rating (breakdown voltage), beyond which they can fail or become damaged, so care must be taken not to exceed this rating.

Conclusion

Capacitors are versatile components that store energy in the form of an electric field, with the amount of stored energy depending on both capacitance and voltage. The formula $U = \frac{1}{2} C V^2$ provides a straightforward method for calculating the energy stored, and understanding this energy storage capacity is essential in designing circuits for applications ranging from power backup and filtering to energy storage in electric vehicles. Capacitors are unique in their ability to discharge energy rapidly, making them indispensable in fields such as electronics, medicine, and renewable energy systems. As technology advances, capacitors continue to play a pivotal role in energy management and the efficient operation of electrical devices.