Exploring Kinetics and Kinematics: Understanding Motion and Forces

Kinetics and kinematics are two essential branches of classical mechanics that play a critical role in understanding motion. While they are often studied together, they focus on different aspects of how objects move. Kinematics deals with describing the motion of objects without considering the forces that cause them, whereas kinetics involves studying the forces and their effects on the motion of objects.

In this article, we’ll explore the fundamental concepts of both kinematics and kinetics, explain their differences, and provide real-world examples to illustrate how these concepts are used to analyze motion in physics, engineering, and everyday life.

Kinematics: Describing Motion Without Forces

Kinematics is the branch of mechanics that focuses on describing the motion of objects using parameters like position, velocity, acceleration, and time. Kinematics does not concern itself with the forces that cause motion; instead, it simply describes how objects move.

Key Concepts in Kinematics:

1. Position ( $x$ ) – The location of an object relative to a reference point.
2. Displacement ( $\Delta x$ ) – The change in position of an object; it is a vector quantity, which means it has both magnitude and direction.
3. Velocity ( $v$ ) – The rate at which an object changes its position; it is also a vector quantity, defined as displacement divided by time.
– Average Velocity: $v_{\text{avg}} = \frac{\Delta x}{\Delta t}$
– Instantaneous Velocity: The velocity of an object at a specific moment in time.
4. Acceleration ( $a$ ) – The rate of change of velocity over time.
– Average Acceleration: $a_{\text{avg}} = \frac{\Delta v}{\Delta t}$
– Instantaneous Acceleration: The acceleration at a particular point in time.

Example 1: A Car Accelerating on a Highway

Imagine a car accelerating from a stoplight. If the car reaches a speed of 60 km/h in 10 seconds, we can calculate its average acceleration:

Initial velocity ( $v_0$ ) = 0 km/h (since the car starts from rest)
Final velocity ( $v$ ) = 60 km/h = 16.67 m/s (converted to meters per second)
Time interval ( 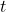$t$ ) = 10 seconds

The formula for acceleration is:

$a = \frac{v - v_0}{t} = \frac{16.67 - 0}{10} = 1.67 \, \text{m/s}^2$

This means the car’s speed increases by 1.67 meters per second every second.

Equations of Motion in Kinematics:

Kinematics provides several equations that describe the relationship between displacement, velocity, acceleration, and time. These equations are especially useful in solving problems involving uniform acceleration:

1. $v = v_0 + at$
2. $x = x_0 + v_0t + \frac{1}{2}at^2$
3. $v^2 = v_0^2 + 2a(x - x_0)$

Example 2: Calculating the Distance a Ball Falls

If you drop a ball from a height, it accelerates downward due to gravity ( $g = 9.8 \, \text{m/s}^2$ ). Suppose you want to know how far the ball falls in 3 seconds.

Using the equation $x = x_0 + v_0t + \frac{1}{2}at^2$ :

Initial position ( 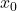$x_0$ ) = 0
Initial velocity ( $v_0$ ) = 0 (since the ball is dropped, not thrown)
Acceleration ( $a$ ) = 9.8 m/s² (gravity)
Time ( 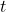$t$ ) = 3 seconds

$x = 0 + 0 + \frac{1}{2}(9.8)(3)^2 = \frac{1}{2} \times 9.8 \times 9 = 44.1 \, \text{m}$

The ball falls 44.1 meters in 3 seconds.

Kinetics: The Study of Forces and Motion

Kinetics, on the other hand, deals with the forces that cause motion. This branch of mechanics focuses on understanding the relationship between the motion of an object and the forces acting on it. In kinetics, we are concerned with concepts like force, mass, momentum, and energy.

Key Concepts in Kinetics:

1. Force ( $F$ ) – A push or pull acting on an object that causes it to accelerate. According to Newton’s Second Law:

$F = ma$

where $m$ is the mass of the object and $a$ is its acceleration.
2. Work ( $W$ ) – The product of force and displacement in the direction of the force:

$W = Fd \cos(\theta)$

where $d$ is displacement and $\theta$ is the angle between the force and displacement vectors.
3. Kinetic Energy ( $KE$ ) – The energy an object has due to its motion:

$KE = \frac{1}{2}mv^2$

4. Potential Energy ( $PE$ ) – The energy stored in an object due to its position or configuration, such as gravitational potential energy:

$PE = mgh$

5. Conservation of Energy – The total energy in a closed system remains constant; energy can neither be created nor destroyed, only transformed from one form to another.

Example 3: A Block on an Inclined Plane

Imagine a block sliding down an inclined plane. To analyze its motion, we need to consider the forces acting on it:

The gravitational force pulling it downward.
The normal force perpendicular to the surface.
The frictional force (if any) opposing its motion.

Using Newton’s Second Law, we can calculate the acceleration of the block down the incline:

$F_{\text{net}} = mg \sin(\theta)$

$a = \frac{F_{\text{net}}}{m} = g \sin(\theta)$

If the incline is frictionless, the block will accelerate down the slope purely due to gravity.

Example 4: Calculating the Force Needed to Stop a Car

A car with a mass of 1,200 kg is moving at a velocity of 20 m/s. If a force of 6,000 N is applied to bring it to a stop, how long will it take?

We can use Newton’s Second Law:

$F = ma \Rightarrow a = \frac{F}{m} = \frac{6000}{1200} = 5 \, \text{m/s}^2$

Now, using the formula $v = v_0 + at$ :

$0 = 20 + (-5)t \Rightarrow t = \frac{20}{5} = 4 \, \text{seconds}$

It will take 4 seconds to bring the car to a stop.

Connecting Kinematics and Kinetics: Understanding Motion in Context

While kinematics focuses on describing motion, kinetics explains the causes behind that motion. To fully understand how objects move, it’s essential to consider both the forces involved and the resulting movement.

Example 5: Projectile Motion

Projectile motion is a classic example where kinematics and kinetics are both essential.

Imagine a ball thrown at an angle $\theta$ with an initial velocity $v_0$ . To analyze its motion, we use:

Kinematics to find the position and velocity of the ball at any point in time.
Kinetics to understand how the force of gravity affects its trajectory.

Using kinematic equations, we can break down the motion into horizontal and vertical components:

Horizontal displacement: $x = v_0 \cos(\theta) t$
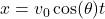
Vertical displacement: $y = v_0 \sin(\theta) t - \frac{1}{2}gt^2$

Example:
If a ball is thrown with an initial speed of 20 m/s at an angle of $30^\circ$ :

Horizontal velocity = $20 \cos(30^\circ) = 17.32 \, \text{m/s}$
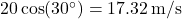
Vertical velocity = $20 \sin(30^\circ) = 10 \, \text{m/s}$

The ball will reach its maximum height when its vertical velocity becomes zero:

$v_y = v_0 \sin(\theta) - gt = 0$

$t = \frac{v_0 \sin(\theta)}{g} = \frac{10}{9.8} \approx 1.02 \, \text{seconds}$

The total time of flight is twice this value, so the ball will be in the air for approximately 2.04 seconds.

Conclusion: Mastering Kinematics and Kinetics

Kinematics and kinetics are complementary branches of mechanics that help us understand how objects move and why they move the way they do. Kinematics focuses on describing motion, using parameters like displacement, velocity, and acceleration, while kinetics deals

with the forces that cause this motion, such as gravity, friction, and applied forces.

From understanding the trajectory of a projectile to calculating the forces required to stop a moving vehicle, mastering the principles of kinematics and kinetics is essential in fields like engineering, physics, sports science, and even everyday problem-solving.

By combining both kinematics and kinetics, we can gain a comprehensive understanding of motion, making it possible to predict, control, and optimize the movement of objects in various real-world scenarios.