Vertical circular motion refers to the movement of an object along a circular path in a vertical plane, where both gravitational and centripetal forces act on the object. This type of motion is common in roller coasters, pendulums, and objects tied to a string being swung in circles. In vertical circular motion, the object’s speed, tension, and the forces acting on it vary at different points along the circular path due to the effects of gravity, resulting in complex dynamics that require detailed analysis.

In this article, we’ll explore the forces involved in vertical circular motion, derive the key equations governing this motion, and discuss various practical examples to illustrate the concept.
Understanding Vertical Circular Motion
In vertical circular motion, an object moves in a circle in a vertical plane, subject to:
- Centripetal Force: The inward force required to keep an object moving in a circular path.
- Gravitational Force: The downward force due to gravity, which varies in effect depending on the object’s position along the path.
The centripetal force in vertical circular motion is not constant, as it depends on the object’s position within the circle. At the top of the circular path, gravity acts in the same direction as the centripetal force, while at the bottom, it acts in the opposite direction. This difference creates variations in the object’s speed and tension in any supporting string or path structure, such as a roller coaster track.
Key Forces in Vertical Circular Motion
To analyze vertical circular motion, we need to consider the following forces at work:
- Gravitational Force (Weight): Given by
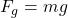 , where
, where 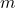 is the mass of the object and
is the mass of the object and 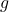 is the gravitational acceleration (approximately 9.8 m/s² near the Earth’s surface).
is the gravitational acceleration (approximately 9.8 m/s² near the Earth’s surface). - Tension Force: In the case of an object attached to a string or a pendulum, the string exerts a tension force that varies along the path, adjusting based on the object’s speed and position within the circle.
- Centripetal Force: The force directed toward the center of the circular path, necessary to keep the object moving in a circle. For an object moving at velocity
 along a circular path with radius
along a circular path with radius  , the centripetal force
, the centripetal force 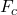 is:
is:
![]()
Position-Dependent Analysis of Forces
In vertical circular motion, the interplay between gravitational force and centripetal force varies at different points in the circle. Below are the forces experienced at specific points along the path:
1. At the Top of the Circle: Both gravitational force and tension work together to provide the required centripetal force. The centripetal force is:
![]()
where ![]() is the tension at the top of the circle,
is the tension at the top of the circle, ![]() is the object’s mass,
is the object’s mass, ![]() is its speed at the top, and
is its speed at the top, and ![]() is the radius.
is the radius.
2. At the Bottom of the Circle: Here, gravitational force acts against the tension, so the centripetal force is given by:
![]()
where ![]() is the tension at the bottom of the circle and
is the tension at the bottom of the circle and ![]() is the speed at the bottom.
is the speed at the bottom.
The tension force at the bottom of the circle is greater than at the top because it must counteract gravity in addition to providing the centripetal force needed for circular motion.
Deriving the Condition for Complete Vertical Circular Motion
For an object to complete a full circle, it must have enough speed at the top of the circle to maintain tension in the string (or sufficient track support for roller coasters). The minimum speed required at the top of the circle, ![]() , ensures that gravity alone can provide the necessary centripetal force if the tension is zero (for the limiting case).
, ensures that gravity alone can provide the necessary centripetal force if the tension is zero (for the limiting case).
1. At the Top (Minimum Speed):
To achieve the minimum speed at the top of the circle, we set the tension ![]() , so gravitational force provides all of the centripetal force:
, so gravitational force provides all of the centripetal force:
![]()
2. Solving for ![]() :
:
![]()
This is the minimum speed needed at the top to maintain the circular path. If the object’s speed at the top is lower than ![]() , it will not complete the circle and will fall under the influence of gravity.
, it will not complete the circle and will fall under the influence of gravity.
3. Speed at the Bottom:
To find the speed at the bottom of the circle, we can apply the conservation of mechanical energy. If the object starts at the top of the circle with the minimum speed ![]() , the total mechanical energy at the top equals the total mechanical energy at the bottom.
, the total mechanical energy at the top equals the total mechanical energy at the bottom.
4. Energy Conservation:
![]()
Since ![]() and
and ![]() , the object’s kinetic energy at the top and bottom, and thus its speed, can be calculated.
, the object’s kinetic energy at the top and bottom, and thus its speed, can be calculated.
Practical Examples of Vertical Circular Motion
Example 1: Roller Coaster Loop
One of the most iconic examples of vertical circular motion is a roller coaster loop. When a roller coaster enters a loop, it moves along a vertical circular path, with gravity affecting its speed at different points along the loop.
- At the Top of the Loop: The roller coaster needs to maintain a minimum speed,
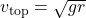 , to stay on track. If it goes slower, it risks falling back, as the centripetal force would be insufficient to keep it moving along the circular path.
, to stay on track. If it goes slower, it risks falling back, as the centripetal force would be insufficient to keep it moving along the circular path. - At the Bottom of the Loop: The speed is at its maximum at the bottom due to gravitational acceleration, and the track must provide the necessary support force to keep the coaster in motion.
This principle is essential in roller coaster design, as it determines the minimum height and speed needed for the coaster to safely navigate the loop without detaching from the track.
Example 2: Pendulum Swing
A pendulum exhibits vertical circular motion as it swings through its arc. The highest point in the swing, or the apex, can be treated as the “top” of the circular path, and the lowest point, or nadir, as the “bottom.”
- Top of the Swing: At the top, the speed of the pendulum is lowest, and gravity acts as a component of the centripetal force.
- Bottom of the Swing: At the bottom of the swing, the speed is highest due to the gravitational potential energy being fully converted to kinetic energy. The tension in the string is at its maximum here, as it must counteract gravity and provide the centripetal force for circular motion.
Example 3: A Stone Tied to a String
Imagine swinging a stone tied to a string in a vertical circle. The forces acting on the stone vary as it moves through the circle:
- Top of the Circle: At the highest point, gravity helps provide the centripetal force. To keep the stone moving, it must have a minimum speed of
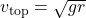 .
. - Bottom of the Circle: At the lowest point, the stone’s speed increases due to gravitational acceleration. The tension in the string reaches its peak here to counter both the weight of the stone and provide the centripetal force.
If the stone’s speed at the top of the path falls below ![]() , it will lose tension, resulting in a fall.
, it will lose tension, resulting in a fall.
Example 4: Loop-the-Loop in a Toy Car Track
In a toy car track with a loop-the-loop, the car exhibits vertical circular motion as it travels through the loop. Similar to the roller coaster, the car must have a minimum speed at the top to complete the loop.
- Top of the Loop: The car must travel at or above
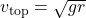 to avoid falling out of the loop.
to avoid falling out of the loop. - Energy Conservation: If the car starts from a height sufficient to convert potential energy to kinetic energy, it will gain the required speed as it descends and reach the loop’s bottom with maximum speed.
Designing such a toy track requires careful consideration of height, track material, and car speed to ensure it achieves sufficient energy to make it through the loop.
Limitations and Assumptions in Vertical Circular Motion
The analysis of vertical circular motion assumes several ideal conditions, which may not hold perfectly in real-world scenarios:
- Neglecting Air Resistance: Air resistance, which can significantly affect the motion at higher speeds, is typically ignored in theoretical calculations.
- String/Tension Limitations: In cases where an object is attached to a string, the string has a maximum tensile strength. If the required tension exceeds this strength, the string may break.
- Frictionless Path: In scenarios like roller coasters, calculations often assume frictionless tracks, which is an approximation; friction usually reduces the system’s energy over time.
Conclusion
Vertical circular motion illustrates the interplay of gravitational and centripetal forces in maintaining an object’s path along a circular trajectory. By understanding the variations in speed, tension, and force at different points within the circle, we gain insight into many natural and engineered systems, such as pendulums, roller coasters, and other objects that operate under gravitational influence. The concepts outlined in vertical circular motion are essential in physics and engineering, guiding design and analysis in various applications, from amusement parks to dynamic mechanical systems.