Gauss’s Law is a fundamental principle in electromagnetism, relating the electric flux through a closed surface to the charge enclosed by that surface. Named after the German mathematician and physicist Carl Friedrich Gauss, Gauss’s Law is one of Maxwell’s four equations, which describe classical electromagnetism. The law simplifies the calculation of electric fields around symmetrical charge distributions, making it a powerful tool in physics and engineering.

This article provides an in-depth exploration of Gauss’s Law, including its mathematical formulation, conceptual basis, applications, and examples to illustrate its practical use.
1. Understanding Gauss’s Law
At its core, Gauss’s Law relates the electric flux passing through a closed surface to the total electric charge enclosed within that surface. Electric flux is a measure of the quantity of electric field lines passing through a given surface, and Gauss’s Law allows us to understand how these lines relate to the charges that generate them.
Mathematically, Gauss’s Law is expressed as:
![]()
where:
- Φ_E is the electric flux through a closed surface
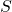 ,
, 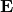 is the electric field vector,
is the electric field vector,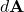 is a vector representing an infinitesimal area on the surface, pointing outward,
is a vector representing an infinitesimal area on the surface, pointing outward, is the total charge enclosed within the surface
is the total charge enclosed within the surface 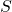 , and
, and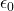 is the permittivity of free space, approximately
is the permittivity of free space, approximately 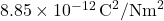 .
.
In simple terms, Gauss’s Law states that the total electric flux through a closed surface is proportional to the total charge enclosed within that surface. If there are no charges within the surface, the net flux is zero, even if an electric field exists outside the surface.
2. Conceptual Basis of Gauss’s Law
Gauss’s Law is rooted in the concept of field lines and their relationship with electric charges. Electric field lines originate from positive charges and terminate at negative charges. The density of these field lines represents the strength of the electric field, and the flux through a surface represents the number of field lines passing through that surface.
a. Electric Flux
Electric flux measures the total electric field passing through a given surface. The flux through a small area element ![]() on the surface is given by:
on the surface is given by:
![]()
where:
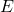 is the magnitude of the electric field,
is the magnitude of the electric field,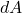 is the magnitude of the area element,
is the magnitude of the area element,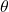 is the angle between
is the angle between 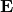 and the normal to the surface.
and the normal to the surface.
For a closed surface, the electric flux is calculated by integrating this quantity over the entire surface. When the electric field is perpendicular to the surface and uniform, the flux is simply ![]() .
.
b. Permittivity of Free Space (ε₀)
The permittivity of free space, ε₀, is a fundamental physical constant that describes how electric fields interact with the vacuum of free space. Gauss’s Law shows that ε₀ plays a role in determining how much electric flux results from a given charge. In materials, the permittivity changes depending on the material’s properties, which can influence electric flux and field strength.
3. Applications of Gauss’s Law
Gauss’s Law is particularly useful in calculating electric fields in cases of high symmetry, such as spherical, cylindrical, or planar charge distributions. By choosing appropriate Gaussian surfaces that match the symmetry of the charge distribution, the law enables simplified calculations of electric fields.
a. Electric Field of a Point Charge
The electric field of a point charge ![]() can be easily derived using Gauss’s Law. Consider a point charge located at the center of a spherical Gaussian surface of radius
can be easily derived using Gauss’s Law. Consider a point charge located at the center of a spherical Gaussian surface of radius ![]() .
.
Since the electric field from a point charge is radially symmetric, we can assume that the electric field ![]() is the same at all points on the surface of the sphere and points directly outward.
is the same at all points on the surface of the sphere and points directly outward.
Applying Gauss’s Law:
![]()
Solving for ![]() , we get:
, we get:
![]()
This result confirms Coulomb’s Law for the electric field of a point charge, showing that Gauss’s Law can yield fundamental results in electromagnetism.
Example:
In atomic physics, this derivation is useful for calculating the electric field around an electron or proton, where we treat each particle as a point charge. The resulting field can explain the electrostatic forces between subatomic particles.
b. Electric Field of a Spherically Symmetric Charge Distribution
For a spherically symmetric charge distribution, such as a uniformly charged sphere, Gauss’s Law simplifies the calculation of electric fields both inside and outside the sphere.
For a sphere with radius ![]() and total charge
and total charge ![]() , two cases emerge:
, two cases emerge:
1. Outside the sphere (![]() ): The charge distribution behaves as if all the charge were concentrated at the center.
): The charge distribution behaves as if all the charge were concentrated at the center.
Applying Gauss’s Law:
![]()
2. Inside the sphere (![]() ): Here, the electric field depends on the enclosed charge, which varies with the radius
): Here, the electric field depends on the enclosed charge, which varies with the radius ![]() .
.
If the charge density ![]() is uniform, the enclosed charge
is uniform, the enclosed charge ![]() within radius
within radius ![]() is:
is:
![]()
Applying Gauss’s Law:
![]()
This linear dependence on ![]() shows that the electric field increases linearly from zero at the center of the sphere to its maximum at the surface.
shows that the electric field increases linearly from zero at the center of the sphere to its maximum at the surface.
Example:
This derivation is useful in fields such as astrophysics and geophysics to calculate the gravitational field inside massive celestial objects, such as stars or planets, which often exhibit spherically symmetric mass distributions.
c. Electric Field of a Line of Charge
Gauss’s Law is also helpful for finding the electric field around a long, straight line of charge. In this case, a cylindrical Gaussian surface aligned with the line of charge is ideal for calculation, as the symmetry simplifies the math.
Let ![]() represent the linear charge density (charge per unit length) of the line of charge. Using a cylindrical Gaussian surface with radius
represent the linear charge density (charge per unit length) of the line of charge. Using a cylindrical Gaussian surface with radius ![]() and length
and length ![]() :
:
![]()
Solving for ![]() , we find:
, we find:
![]()
This result shows that the electric field around a line of charge decreases with distance as ![]() , illustrating how charge distribution affects field strength in cylindrical symmetry.
, illustrating how charge distribution affects field strength in cylindrical symmetry.
Example:
This calculation is useful in understanding the electric field around high-voltage power lines, which carry large amounts of charge and can influence the surrounding environment.
d. Electric Field of a Plane of Charge
For a uniformly charged infinite plane, Gauss’s Law allows us to calculate the electric field near the plane without integrating across the entire plane.
Assume a plane with a surface charge density ![]() (charge per unit area). By choosing a cylindrical Gaussian surface that intersects the plane perpendicularly:
(charge per unit area). By choosing a cylindrical Gaussian surface that intersects the plane perpendicularly:
![]()
Solving for ![]() , we obtain:
, we obtain:
![]()
This result is notable because it implies that the electric field near an infinite plane of charge is constant and independent of distance from the plane.
Example:
This derivation is used in capacitor design, where two parallel plates are treated as infinite planes. The uniform electric field between these plates enables efficient storage and transfer of electrical energy in electronic devices.
4. Advantages and Limitations of Gauss’s Law
While Gauss’s Law is a powerful tool for calculating electric fields, it is most effective in cases of high symmetry (spherical, cylindrical, or planar). In asymmetric charge distributions, direct application of Gauss’s Law may be impractical, and numerical methods or other techniques may be necessary.
Advantages:
- Simplifies Calculations: For symmetrical charge distributions, Gauss’s Law simplifies the computation of electric fields, reducing the need for complex integrals.
- Useful in Theory and Practice
: It provides insights into fundamental properties of electric fields and aids in designing devices like capacitors, charged spheres, and wires.
Limitations:
- Limited to Symmetrical Cases: Gauss’s Law is only practical for calculating fields with high symmetry. For irregular charge distributions, its use is limited.
- Assumes Static Fields: Gauss’s Law applies to electrostatic fields; dynamic (changing) electric fields require Maxwell’s full set of equations.
5. Gauss’s Law and Maxwell’s Equations
Gauss’s Law is one of the four Maxwell’s equations that form the foundation of classical electromagnetism. These equations collectively describe how electric and magnetic fields interact and propagate. In this context, Gauss’s Law for electricity states that the electric flux through a closed surface is proportional to the enclosed charge, highlighting the relationship between charge and electric field.
The integral form of Gauss’s Law makes it clear that charge distributions influence electric fields, while the differential form (derived via Gauss’s theorem) connects the electric field divergence to the charge density:
![]()
This formulation provides insights into how electric fields diverge from points of charge density, contributing to a broader understanding of electric and magnetic phenomena.
Conclusion
Gauss’s Law is a cornerstone of electromagnetism, providing a simple yet powerful approach to understanding electric fields in relation to charge distributions. From calculating the electric field of point charges and infinite planes to deriving fundamental properties in electrostatics, Gauss’s Law is an invaluable tool for physicists and engineers. Its applications in fields like electronics, geophysics, and astrophysics underscore its versatility, making it essential for both theoretical research and practical design in modern science and technology.