Gerak Lurus Berubah Beraturan: Konsep dan Aplikasinya

Gerak Lurus Berubah Beraturan (GLBB) adalah salah satu jenis gerak dalam fisika di mana suatu objek bergerak dalam lintasan lurus dengan percepatan konstan. GLBB penting untuk memahami fenomena fisika yang lebih kompleks dan aplikasinya dalam kehidupan sehari-hari. Artikel ini akan membahas definisi, karakteristik, persamaan, dan contoh aplikasi GLBB.

Definisi Gerak Lurus Berubah Beraturan

Gerak Lurus Berubah Beraturan didefinisikan sebagai gerak suatu objek dalam lintasan lurus dengan percepatan tetap ( $a$ ). Dalam GLBB, kecepatan objek berubah secara linier terhadap waktu karena adanya percepatan konstan.

Persamaan Dasar GLBB

Dalam GLBB, terdapat beberapa persamaan kunci yang menghubungkan posisi ( $x$ ), kecepatan ( $v$ ), percepatan ( $a$ ), dan waktu ( $t$ ):

1. Persamaan posisi sebagai fungsi waktu:

$x = x_0 + v_0 t + \frac{1}{2} a t^2$

2. Persamaan kecepatan sebagai fungsi waktu:

$v = v_0 + a t$

3. Persamaan kecepatan sebagai fungsi posisi:

$v^2 = v_0^2 + 2 a (x - x_0)$

di mana:

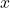$x$ adalah posisi akhir objek (meter, m),
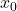$x_0$ adalah posisi awal objek (meter, m),
$v$ adalah kecepatan akhir objek (meter per detik, m/s),
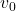$v_0$ adalah kecepatan awal objek (meter per detik, m/s),
$a$ adalah percepatan konstan objek (meter per detik kuadrat, m/s²),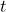
$t$ adalah waktu (detik, s).

Karakteristik Gerak Lurus Berubah Beraturan

1. Percepatan Konstan: Percepatan ( $a$ ) tetap konstan sepanjang gerak.
2. Lintasan Lurus: Objek bergerak dalam garis lurus.
3. Kecepatan Berubah Linear: Kecepatan objek berubah secara linier terhadap waktu.

Contoh Perhitungan GLBB

Contoh 1: Mobil yang Dipercepat

Misalkan sebuah mobil awalnya bergerak dengan kecepatan 20 m/s dan kemudian dipercepat dengan percepatan konstan 2 m/s². Hitung kecepatan mobil setelah 5 detik.

Menggunakan persamaan kecepatan:

$v = v_0 + a t$

$v = 20 \, \text{m/s} + 2 \, \text{m/s}^2 \times 5 \, \text{detik} = 20 \, \text{m/s} + 10 \, \text{m/s} = 30 \, \text{m/s}$

Contoh 2: Objek Jatuh Bebas

Sebuah benda dijatuhkan dari ketinggian 45 meter tanpa kecepatan awal (mengabaikan resistensi udara). Hitung waktu yang diperlukan untuk mencapai tanah dan kecepatan saat mencapai tanah. Menggunakan percepatan gravitasi $g = 9.8 \, \text{m/s}^2$ .

Menggunakan persamaan posisi:

$x = x_0 + v_0 t + \frac{1}{2} g t^2$

$0 = 45 + 0 + \frac{1}{2} \times (-9.8) t^2$

$-45 = -4.9 t^2$

$t^2 = \frac{45}{4.9}$

$t \approx 3 \, \text{detik}$

Menggunakan persamaan kecepatan:

$v = v_0 + g t$

$v = 0 + 9.8 \times 3 = 29.4 \, \text{m/s}$

Aplikasi Gerak Lurus Berubah Beraturan

1. Transportasi

Dalam desain sistem pengereman kendaraan, GLBB digunakan untuk menghitung jarak berhenti dan waktu yang dibutuhkan untuk berhenti dengan percepatan negatif konstan.

2. Olahraga

GLBB diterapkan dalam olahraga untuk analisis gerak atlet, seperti pelari yang mempercepat atau memperlambat kecepatannya selama lomba.

3. Astronomi

Dalam peluncuran roket dan pergerakan planet, GLBB membantu dalam menghitung lintasan dan kecepatan objek di luar angkasa.

4. Teknologi dan Rekayasa

GLBB digunakan dalam desain mekanisme seperti katrol dan mesin yang melibatkan percepatan konstan.

Grafis GLBB

Grafik Posisi vs. Waktu

Dalam GLBB, grafik posisi (x) terhadap waktu (t) adalah kurva parabola yang menunjukkan perubahan posisi dengan percepatan konstan.

Grafik Kecepatan vs. Waktu

Dalam GLBB, grafik kecepatan (v) terhadap waktu (t) adalah garis lurus yang menunjukkan perubahan kecepatan linier.

html

Kesimpulan

Gerak Lurus Berubah Beraturan adalah gerak dengan lintasan lurus dan percepatan konstan. Konsep ini sangat penting dalam fisika dan aplikasinya meliputi berbagai bidang seperti transportasi, olahraga, astronomi, dan teknologi. Memahami GLBB memungkinkan kita untuk menganalisis dan memprediksi pergerakan objek dalam berbagai situasi.

Referensi

1. Tipler, P. A., & Mosca, G. (2008). Physics for Scientists and Engineers. W.H. Freeman. ISBN: 978-1429201247.
2. Halliday, D., Resnick, R., & Walker, J. (2013). Fundamentals of Physics. Wiley. ISBN: 978-1118230718.
3. Serway, R. A., & Jewett, J. W. (2018). Physics for Scientists and Engineers with Modern Physics. Cengage Learning. ISBN: 978-1337553292.
4. Giancoli, D. C. (2014). Physics: Principles with Applications. Pearson. ISBN: 978-0321625922.

FAQ tentang Gerak Lurus Berubah Beraturan

Apa yang dimaksud dengan gerak lurus berubah beraturan (GLBB)?

Gerak lurus berubah beraturan adalah gerakan suatu objek yang berlangsung dalam garis lurus dengan percepatan konstan. Dalam GLBB, kecepatan objek berubah secara teratur seiring waktu.

Apa ciri-ciri gerak lurus berubah beraturan?

1. Percepatan Konstan: Objek mengalami percepatan tetap.
2. Kecepatan Berubah: Kecepatan objek meningkat atau menurun secara teratur.
3. Jarak yang Ditempuh: Jarak yang ditempuh tidak sebanding dengan waktu; semakin lama waktu, semakin jauh jarak yang ditempuh.

Bagaimana cara menghitung jarak dalam GLBB?

Jarak yang ditempuh dalam gerak lurus berubah beraturan dapat dihitung dengan rumus:

$s = vt + \frac{1}{2}at^2$

di mana $s$ adalah jarak, $v$ adalah kecepatan awal, $a$ adalah percepatan, dan $t$ adalah waktu.

Apa contoh situasi yang menunjukkan GLBB?

Contoh gerak lurus berubah beraturan termasuk:

Mobil yang mulai bergerak dari diam dan mempercepat di jalan lurus.
Bola yang jatuh bebas dari ketinggian, dipengaruhi oleh gravitasi.

Bagaimana cara menghitung kecepatan akhir dalam GLBB?

Kecepatan akhir dalam GLBB dapat dihitung dengan rumus:

$v = v_0 + at$

di mana $v$ adalah kecepatan akhir, $v_0$ adalah kecepatan awal, $a$ adalah percepatan, dan $t$ adalah waktu.

Apa yang terjadi jika percepatan negatif dalam GLBB?

Jika percepatan negatif, berarti objek mengalami deselerasi atau perlambatan. Dalam hal ini, kecepatan objek akan menurun seiring waktu.

Mengapa penting memahami gerak lurus berubah beraturan?

Memahami GLBB penting karena ini merupakan dasar dari banyak fenomena fisika yang lebih kompleks. Konsep ini digunakan dalam berbagai aplikasi teknik, analisis gerakan, dan perencanaan transportasi.