Height and distance calculations are an important aspect of trigonometry, allowing us to solve real-world problems involving angles and measurements, such as calculating the height of buildings, distances across rivers, or the length of shadows. These problems often involve angles of elevation and depression, which can be determined using trigonometric ratios such as sine, cosine, and tangent. This article explores these concepts, essential formulas, and examples to show how height and distance calculations are applied practically.

Understanding Angles of Elevation and Depression
1. Angle of Elevation:
- When an observer looks up from a horizontal line to an object, the angle formed between the horizontal line and the line of sight to the object is called the angle of elevation.
- Example: Imagine you’re standing on the ground and looking up at the top of a tree. The angle your line of sight makes with the horizontal ground is the angle of elevation.
2. Angle of Depression:
- Conversely, when an observer looks down from a horizontal line to an object below, the angle between the horizontal line and the line of sight is called the angle of depression.
- Example: If you’re standing at the top of a building and looking down at a car on the street, the angle your line of sight makes with the horizontal is the angle of depression.
Trigonometric Ratios Used in Height and Distance Calculations
In problems involving height and distance, we often use trigonometric ratios to relate angles and side lengths. Here’s a quick review of the basic trigonometric ratios:
1. Sine:
- For a right triangle, the sine of an angle
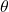 is defined as:
is defined as:
![]()
2. Cosine:
- The cosine of an angle
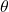 is defined as:
is defined as:
![]()
3. Tangent:
- The tangent of an angle
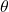 is defined as:
is defined as:
![]()
The tangent ratio is particularly useful in height and distance problems since it directly relates the opposite side (height) to the adjacent side (distance).
Using the Tangent Ratio for Height and Distance Problems
In most height and distance problems, we know the angle of elevation or depression and either the height or the horizontal distance. The tangent ratio becomes the main tool for solving these problems.
Basic Formula for Height and Distance
For an angle of elevation ![]() , if we know the horizontal distance
, if we know the horizontal distance ![]() from the observer to the object and want to find the height
from the observer to the object and want to find the height ![]() of the object, we use:
of the object, we use:
![]()
Conversely, if we know the height ![]() and want to find the distance
and want to find the distance ![]() :
:
![]()
Example Problems in Height and Distance
Let’s explore some practical examples that apply these concepts and formulas.
Example 1: Finding the Height of a Building
Problem: You are standing 50 meters away from the base of a building. The angle of elevation to the top of the building is ![]() . What is the height of the building?
. What is the height of the building?
Solution:
- Given:
- Distance
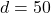 meters
meters - Angle of elevation
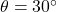
- To find the height
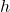 of the building, we use:
of the building, we use:
![]()
![]()
Using ![]() ,
,
![]()
- The height of the building is approximately 28.85 meters.
Example 2: Calculating Distance to a Point Across a River
Problem: A person standing on one bank of a river observes a tree directly across on the opposite bank. The angle of elevation to the top of the tree is ![]() , and the height of the tree is 20 meters. What is the width of the river?
, and the height of the tree is 20 meters. What is the width of the river?
Solution:
- Given:
- Height of the tree
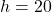 meters
meters - Angle of elevation
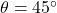
- To find the distance
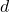 (width of the river):
(width of the river):
![]()
![]()
Since ![]() ,
,
![]()
- The width of the river is 20 meters.
Example 3: Using the Angle of Depression
Problem: From the top of a lighthouse 60 meters tall, the angle of depression to a boat on the sea is ![]() . Find the horizontal distance from the base of the lighthouse to the boat.
. Find the horizontal distance from the base of the lighthouse to the boat.
Solution:
- Given:
- Height
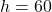 meters
meters - Angle of depression
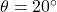
- Since the angle of depression from the top of the lighthouse to the boat is
 , the angle of elevation from the boat to the top of the lighthouse is also
, the angle of elevation from the boat to the top of the lighthouse is also  .
. - To find the horizontal distance
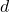 :
:
![]()
![]()
Using ![]() ,
,
![]()
- The horizontal distance from the lighthouse to the boat is approximately 164.84 meters.
Applications of Height and Distance in Real Life
Height and distance calculations are practical in various fields, from surveying and construction to navigation and aerial navigation. Below are some key applications:
1. Surveying and Mapping:
- Surveyors use trigonometry to measure distances and elevations when creating maps or surveying land. Angles of elevation and depression allow them to estimate the height of mountains, depth of valleys, and distance across rivers without crossing these physical obstacles.
2. Construction and Architecture:
- Architects and construction engineers rely on trigonometric calculations to design structures with specific heights and slopes. For instance, calculating the angle for a sloped roof or determining the length of a ramp requires trigonometry to ensure safety and accuracy in construction.
3. Aviation:
- Pilots use height and distance calculations to determine their altitude relative to the ground and the horizontal distance to landing points. When landing, the angle of descent is carefully calculated using trigonometric principles to ensure a safe approach.
4. Astronomy:
- Astronomers calculate distances to celestial bodies using trigonometric methods such as parallax, where they measure the apparent shift in a star’s position from different points in Earth’s orbit to estimate its distance.
Additional Height and Distance Formulas
While the tangent ratio is primarily used in height and distance problems, other trigonometric functions are useful in various scenarios:
1. Using Sine and Cosine for Inclined Distances:
- When an object or person is on an inclined plane, the height can be determined using the sine function:
![]()
- The horizontal component can be determined using the cosine function:
![]()
2. Multiple Angles of Elevation:
- In some cases, you may have two angles of elevation from two different points to the top of an object. Using trigonometric ratios, you can calculate the height and distance of the object from either point. This technique is often used in surveying to calculate the height of inaccessible objects.
Example: Multiple Angles of Elevation
Problem: Two observers are standing 100 meters apart. Observer A sees the top of a tree at an angle of elevation of ![]() , and Observer B, closer to the tree, sees it at
, and Observer B, closer to the tree, sees it at ![]() . Calculate the height of the tree.
. Calculate the height of the tree.
Solution:
- Let
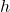 be the height of the tree, and
be the height of the tree, and 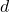 be the distance from Observer B to the base of the tree.
be the distance from Observer B to the base of the tree. - From Observer B:
![]()
Since ![]() ,
,
![]()
- From Observer A (100 meters away from Observer B):
![]()
Since ![]() ,
,
![]()
- Equating the two expressions for
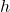 :
:
![]()
Solving this equation yields ![]() meters, and substituting back, we find
meters, and substituting back, we find ![]() meters.
meters.
Conclusion
The concepts of height and distance in trigonometry provide powerful tools for solving real-world problems. By using trigonometric ratios and angles of elevation and depression, we can calculate heights, distances, and inclines accurately without needing direct measurements. These applications are essential across fields like surveying, aviation, architecture, and astronomy. The principles of height and distance calculations are integral to understanding and interpreting spatial relationships, making trigonometry a valuable asset in both theoretical and practical contexts.