Impending Motion: Concept, Forces, and Applications in Physics and Engineering

Impending motion refers to the condition in which an object is on the verge of moving but has not yet started moving. This state is of interest in physics and engineering because it helps in understanding the forces at play just before motion occurs. Typically, impending motion involves a balance between the applied force and the maximum static frictional force, which prevents the object from sliding or moving.

This article explains the concept of impending motion, explores the forces involved, derives conditions for impending motion, and illustrates its significance in practical applications.

Understanding Impending Motion

Impending motion describes the condition where an object is about to move but remains stationary due to the resistance of static friction or other balancing forces. In simple terms, the object is “on the brink” of movement, where the applied force is equal to the maximum resistance offered by friction or any other opposing force. This condition is crucial in understanding how forces interact in mechanical systems and plays a role in the design and analysis of machines, structures, and materials.

Key Characteristics of Impending Motion

1. Maximum Static Friction: Impending motion is observed when the applied force equals the maximum static frictional force between two surfaces in contact.
2. Equilibrium Condition: The object remains in static equilibrium, with all forces balanced, but any slight increase in applied force would initiate motion.
3. Threshold of Motion: Impending motion represents the threshold at which the transition from static friction to kinetic friction occurs.

Example: Consider a box resting on a horizontal floor. If you gradually apply force to the box, there will be a point where the box is about to slide but does not actually move. This is the state of impending motion, where the applied force matches the maximum static frictional force that resists movement.

Forces Involved in Impending Motion

Impending motion primarily involves the interaction between the applied force and the maximum static frictional force. Other forces, such as gravity, normal force, and tension (in cases of inclined planes or ropes), may also be present.

Static Friction Force

Static friction is the force that resists the relative motion of two surfaces in contact when there is no movement. The static frictional force ( $F_s$ ) acts opposite to the direction of the applied force and is given by:

$F_s = \mu_s N$

where:

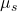$\mu_s$ is the coefficient of static friction, which depends on the materials and surface roughness of the contacting surfaces.
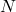$N$ is the normal force, which is the perpendicular force exerted by a surface to support the weight of the object.

In impending motion, the static friction force reaches its maximum possible value ( $F_{s,\text{max}} = \mu_s N$ ), as the applied force tries to overcome this maximum threshold.

Normal Force

The normal force ( $N$ ) is the perpendicular force exerted by a surface to support the weight of an object resting on it. For an object resting on a horizontal surface, the normal force is equal to the gravitational force ( $mg$ ), where $m$ is the mass of the object and $g$ is the acceleration due to gravity. On an inclined surface, the normal force is adjusted based on the angle of inclination.

Applied Force

The applied force ( $F$ ) is the external force exerted on the object to cause motion. For impending motion, the applied force equals the maximum static frictional force, and any increase in this force will overcome the static friction, initiating movement.

Conditions for Impending Motion

For an object to be in impending motion, the following conditions must be satisfied:

1. Equality of Applied Force and Maximum Static Friction:

$F = \mu_s N$

2. Force Balance in the Vertical Direction (for horizontal surfaces):

$N = mg$

For inclined surfaces or systems involving additional forces (such as tension or angle components), the balance of forces must include those additional factors.

Example Calculation of Impending Motion on a Horizontal Surface

Suppose a 10 kg block rests on a horizontal surface with a coefficient of static friction $\mu_s = 0.4$ . To find the force needed to bring the block to the point of impending motion:

1. Calculate the normal force $N$ :

$N = mg = 10 \times 9.8 = 98 \, \text{N}$

2. Determine the maximum static friction $F_{s,\text{max}}$ :

$F_{s,\text{max}} = \mu_s N = 0.4 \times 98 = 39.2 \, \text{N}$

Thus, an applied force of 39.2 N is required to reach the point of impending motion. Any force above 39.2 N will initiate movement.

Impending Motion on an Inclined Plane

When an object is placed on an inclined plane, the angle of inclination affects the forces involved in impending motion. In this case, the forces acting on the object are:

1. Gravitational Force ( $mg$ ): Acts vertically downward.
2. Normal Force ( $N$ ): Perpendicular to the inclined surface.
3. Component of Gravitational Force along the Incline ( $mg \sin \theta$ ): Causes the object to slide down the incline.
4. Component of Gravitational Force perpendicular to the Incline ( $mg \cos \theta$ ): Balanced by the normal force.

For impending motion on an inclined plane, the frictional force equals the downslope component of gravity:

$F_s = \mu_s N$

Since $N = mg \cos \theta$ , we can express the condition for impending motion as:

$mg \sin \theta = \mu_s mg \cos \theta$

Dividing both sides by $mg$ , we get:

$\tan \theta = \mu_s$

Thus, the angle $\theta$ at which impending motion occurs is given by:

$\theta = \arctan(\mu_s)$

Example Calculation of Impending Motion on an Incline

Suppose a 5 kg block rests on an inclined plane with a coefficient of static friction $\mu_s = 0.3$ . To find the angle $\theta$ at which impending motion occurs:

1. Calculate $\theta$ :

$\theta = \arctan(0.3) \approx 16.7^\circ$

At an angle of approximately $16.7^\circ$ , the block will reach the threshold of impending motion and start to slide if the angle is increased further.

Applications of Impending Motion

Impending motion has practical applications in fields such as mechanical engineering, civil engineering, and robotics. Understanding the threshold at which motion begins is essential for designing and analyzing structures, materials, and systems where static and dynamic forces interact.

1. Structural Engineering

In structural engineering, the concept of impending motion is used in the design of building foundations, retaining walls, and slopes. Engineers must ensure that structures can withstand forces without reaching the threshold of impending motion, which could lead to slippage or collapse.

Example: In retaining walls, engineers calculate the force exerted by soil to ensure that the wall can resist impending motion. By designing the wall to withstand these forces, they prevent soil from sliding and maintain structural stability.

2. Frictional Clutches and Brakes

In automotive and machinery applications, impending motion principles are applied to design clutches and brakes, where controlled friction is essential for safe operation. Clutches and brakes rely on static friction to prevent motion, and impending motion occurs when the applied force equals the maximum frictional resistance.

Example: In a car’s braking system, brake pads apply force to the wheels, creating static friction. When the force approaches the maximum frictional resistance, impending motion occurs, signaling the threshold just before the wheel might start slipping.

3. Conveyor Belts and Transport Systems

In conveyor systems, understanding impending motion is essential for setting the correct load and tension on the belt. If the tension is not sufficient, impending motion could lead to slipping of the conveyor belt relative to the drive rollers, resulting in inefficient operation.

Example: A conveyor belt transporting heavy materials must have sufficient tension to prevent slipping. Engineers calculate the maximum load the belt can handle without reaching impending motion, ensuring smooth operation.

4. Robotics and Grippers

In robotics, impending motion principles are used to design robotic grippers and actuators that apply controlled force without slipping. By applying force just below the threshold of impending motion, robotic grippers can securely hold objects without the risk of dropping them.

Example: A robotic gripper in an assembly line might use sensors to measure the force needed to grip an object without causing impending motion, allowing the robot to hold the object firmly without slippage.

5. Rock and Soil Mechanics

In geotechnical engineering, understanding impending motion is crucial in analyzing landslides, slope stability, and soil retention. Engineers use the principles of impending motion to calculate the angle at which soil or rock masses will start to move, helping to design slope reinforcements and erosion control measures.

Example: In slope stability analysis, engineers calculate the angle of repose, which is the steepest angle at which soil remains stable without impending motion. Reinforcements such as retaining walls are designed based on this angle to prevent landslides.

6. Machine Design and Bearings

In machine design, bearings and joints are designed to handle loads without reaching impending motion conditions that could

lead to slippage and wear. Proper understanding of current loads and impending motion enables engineers to design more durable mechanical parts.

Example: In rotating machinery, bearings support shafts and prevent them from slipping. Engineers design bearings to withstand maximum static friction, ensuring impending motion is avoided under typical operating conditions.

Conclusion

Impending motion is a critical concept in physics and engineering that describes the condition in which an object is on the verge of movement but remains stationary due to static friction or other balancing forces. By understanding the threshold at which motion begins, engineers and physicists can analyze forces and design structures, machines, and systems that operate safely and efficiently. From retaining walls and conveyor belts to robotics and slope stability, the principles of impending motion play an essential role in a wide variety of practical applications. Accurate calculations and careful design based on impending motion ensure that structures and devices perform reliably under static and dynamic loads, making impending motion a vital consideration in mechanical and structural engineering.