Integers: Definition, Properties, and Applications in Mathematics

Integers are a fundamental set of numbers that form the basis for various mathematical operations and concepts. These numbers include positive and negative whole numbers, as well as zero, extending infinitely in both directions on the number line. Integers allow us to represent quantities, perform arithmetic operations, and solve equations, making them essential for everything from simple calculations to complex problem-solving in mathematics.

In this article, we will dive deep into the concept of integers, exploring their properties, arithmetic operations, and applications, with examples to illustrate each concept.

What Are Integers?

Integers are numbers that consist of positive whole numbers, negative whole numbers, and zero. The set of integers is typically represented by the symbol $\mathbb{Z}$ , derived from the German word “Zahlen,” meaning “numbers.”

The set of integers includes:

Positive integers: 1, 2, 3, 4, …
Negative integers: -1, -2, -3, -4, …
Zero: 0

Mathematically, the set of integers can be written as:

$\mathbb{Z} = \{ ..., -3, -2, -1, 0, 1, 2, 3, ... \}$

Unlike whole numbers or natural numbers, integers encompass both positive and negative values, allowing us to describe quantities in terms of both gain and loss, above and below, or increase and decrease.

Example: Integers in Everyday Contexts

Integers frequently appear in real-life situations. Some examples include:

Temperature: When we say the temperature is -5°C, we’re using a negative integer to represent degrees below zero.
Financial transactions: A deposit of 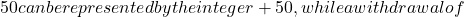$50 can be represented by the integer +50, while a withdrawal of$ 20 is represented by -20.
Elevation: An elevation of 200 feet above sea level can be represented by +200, whereas a depth of 50 feet below sea level would be -50.

Properties of Integers

Integers follow several key properties, especially when it comes to operations like addition, subtraction, multiplication, and division.

1. Closure Property

The closure property states that when we add, subtract, or multiply two integers, the result will always be another integer.

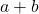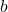Addition: $a + b$ is an integer if $a$ and $b$ are integers.

– Example: $5 + (-3) = 2$ , which is an integer.

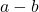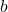Subtraction: $a - b$ is an integer if $a$ and $b$ are integers.

– Example: $7 - (-2) = 9$ , which is an integer.

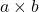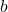Multiplication: $a \times b$ is an integer if $a$ and $b$ are integers.

– Example: $-4 \times 3 = -12$ , which is an integer.

However, division does not always result in an integer, as some integers divided by others can yield fractions or decimals.

2. Commutative Property

The commutative property applies to addition and multiplication of integers but not to subtraction or division. This property states that changing the order of the operands does not affect the result.

Addition: $a + b = b + a$

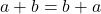
– Example: $4 + (-5) = -5 + 4 = -1$ .

Multiplication: $a \times b = b \times a$

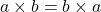
– Example: $3 \times (-2) = -2 \times 3 = -6$ .

Subtraction and division are not commutative:

Subtraction: $5 - 3 \neq 3 - 5$
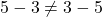
Division: $10 / 2 \neq 2 / 10$

3. Associative Property

The associative property applies to the addition and multiplication of integers, meaning that grouping of numbers does not change the result.

Addition: $(a + b) + c = a + (b + c)$

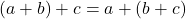
– Example: $(2 + 3) + 4 = 2 + (3 + 4) = 9$ .

Multiplication: $(a \times b) \times c = a \times (b \times c)$

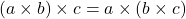
– Example: $(2 \times -3) \times 4 = 2 \times (-3 \times 4) = -24$ .

Subtraction and division are not associative:

Subtraction: $(5 - 3) - 1 \neq 5 - (3 - 1)$
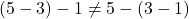
Division: $(8 / 2) / 2 \neq 8 / (2 / 2)$

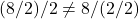
4. Distributive Property

The distributive property allows us to multiply a number by a sum or difference by distributing the multiplication to each term. This property applies to both addition and subtraction.

$a \times (b + c) = (a \times b) + (a \times c)$

Example: $3 \times (4 + 2) = (3 \times 4) + (3 \times 2) = 12 + 6 = 18$ .

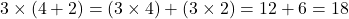5. Identity Property

The identity property states that adding 0 to any integer yields the same integer, and multiplying any integer by 1 also yields the same integer.

Additive Identity: $a + 0 = a$

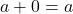
– Example: $-7 + 0 = -7$ .

Multiplicative Identity: $a \times 1 = a$

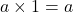
– Example: $4 \times 1 = 4$ .

Operations with Integers

Integers follow specific rules for addition, subtraction, multiplication, and division. Let’s explore each operation and provide examples.

Addition of Integers

The addition of integers is straightforward: adding a positive integer increases the number’s value, while adding a negative integer decreases it.

Adding two positive integers yields a positive result.

– Example: $5 + 3 = 8$

Adding two negative integers yields a negative result.

– Example: $-4 + (-6) = -10$

Adding a positive and a negative integer involves subtraction, with the result taking the sign of the larger absolute value.

– Example: $7 + (-3) = 4$
– Example: $-5 + 8 = 3$

Subtraction of Integers

Subtraction of integers can be thought of as adding the opposite (or additive inverse) of the number being subtracted.

Example: 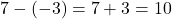$7 - (-3) = 7 + 3 = 10$ (Here, subtracting -3 is equivalent to adding +3).
Example: $-8 - 5 = -8 + (-5) = -13$

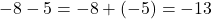
Multiplication of Integers

Multiplication of integers follows specific sign rules:
1. Positive × Positive = Positive
– Example: $4 \times 5 = 20$

2. Negative × Negative = Positive
– Example: $-3 \times -2 = 6$

3. Positive × Negative = Negative
– Example: $6 \times -3 = -18$

Multiplying integers essentially scales the value, with the sign depending on the signs of the operands.

Division of Integers

Division follows similar sign rules as multiplication:
1. Positive ÷ Positive = Positive
– Example: $12 / 3 = 4$

2. Negative ÷ Negative = Positive
– Example: $-15 / -3 = 5$

3. Positive ÷ Negative = Negative
– Example: $18 / -6 = -3$

If division does not yield a whole number, then the result is not considered an integer, as integers do not include fractions or decimals.

The Number Line and Integers

The number line is a visual representation of integers, extending infinitely in both directions:

Positive integers appear to the right of 0.
Negative integers appear to the left of 0.

Each point on the number line represents an integer, and the distance between any two adjacent points is equal to 1. The number line helps visualize operations such as addition and subtraction, making it clear that moving to the right corresponds to increasing (positive) values, while moving to the left corresponds to decreasing (negative) values.

Example: Using the Number Line for Integer Operations

To calculate $-2 + 5$ on the number line:
1. Start at -2.
2. Move 5 steps to the right (since we are adding a positive number).
3. You arrive at +3, so $-2 + 5 = 3$ .

For $4 - 6$ :
1. Start at 4.
2. Move 6 steps to the left (since we are subtracting).
3. You arrive at -2, so $4 - 6 = -2$ .

Applications of Integers

in Real Life

Integers are widely used in various real-world contexts, from measuring temperatures to balancing financial accounts.

1. Weather and Temperature

In meteorology, temperatures can be above or below zero, depending on the climate. Negative integers represent temperatures below freezing.

Example: If the temperature in a city is -5°C in the morning and rises by 8°C, the new temperature is $-5 + 8 = 3^\circ \text{C}$ .

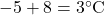2. Banking and Finance

In banking, deposits and withdrawals are represented by positive and negative integers, respectively. Balancing accounts involves adding and subtracting these amounts to determine overall balance.

Example: If you have a balance of 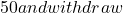$50 and withdraw$ 20, your new balance is 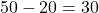$50 - 20 = 30$ dollars.

3. Engineering and Elevation

Engineers often use integers to represent heights above and below a reference point. In surveying, elevations above sea level are positive, and depths below sea level are negative.

Example: A submarine diving 200 feet below sea level can be represented as -200 feet, while a mountain 1,000 feet above sea level is +1000 feet.

4. Sports Scores and Gains/Losses

In games and sports, positive and negative integers represent scores, gains, and losses, especially in games with points systems.

Example: In golf, a score of -3 indicates three strokes under par, while +2 means two strokes over par.

Conclusion: The Importance of Integers

Integers are integral to mathematics, serving as the foundation for operations in arithmetic, algebra, and calculus. Their unique properties and behaviors under operations like addition, subtraction, multiplication, and division make them essential for accurately representing real-world quantities and changes in value. From financial calculations to temperature changes, integers help us model and solve various problems, making them indispensable in both theoretical and practical contexts. Whether on a number line or in applied mathematics, integers remain a cornerstone of mathematical understanding.