Kinematics of Circular Motion: Understanding the Concepts and Applications

Kinematics of circular motion studies the movement of objects following a circular path and focuses on describing their velocity, acceleration, and the forces involved in maintaining circular motion. Unlike linear motion, circular motion requires continuous change in direction, making it unique and applicable to a wide variety of real-life systems, such as the rotation of planets, vehicle movement on curved roads, and the operation of centrifuges.

This article will explain the kinematics of circular motion, covering key concepts like angular velocity, centripetal force, and examples to illustrate each concept.

Understanding Circular Motion

Circular motion occurs when an object moves along a circular path around a fixed central point. In such motion, the object’s direction continuously changes even if its speed remains constant. This constant change in direction requires a force directed toward the center of the circle, known as the centripetal force.

Two types of circular motion exist:

1. Uniform Circular Motion: The object moves at a constant speed around a circular path.
2. Non-Uniform Circular Motion: The object’s speed varies as it travels around the circular path.

The analysis of circular motion often involves variables such as angular displacement, angular velocity, and angular acceleration, which describe the motion in terms of angles rather than linear distances.

Angular Displacement

Angular displacement refers to the angle by which an object moves around a circular path over a given time period. Unlike linear displacement, which measures movement along a straight line, angular displacement measures the rotation angle. Angular displacement is often denoted by the Greek letter $\theta$ and is measured in radians.

Formula:

$\theta = \frac{s}{r}$

where:

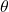$\theta$ is the angular displacement (in radians),
$s$ is the arc length or distance traveled along the circle, and
$r$ is the radius of the circular path.

Example:

If an object moves 5 meters along a circular path with a radius of 2 meters, the angular displacement is:

$\theta = \frac{5}{2} = 2.5 \text{ radians}$

Angular Velocity

Angular velocity describes the rate of change of angular displacement over time. It measures how quickly an object rotates around a circular path and is denoted by the symbol $\omega$ . Angular velocity is typically measured in radians per second (rad/s).

Formula:

$\omega = \frac{\theta}{t}$

where:

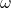$\omega$ is the angular velocity,
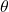$\theta$ is the angular displacement, and
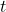$t$ is the time taken.

Relationship Between Linear and Angular Velocity:

If an object moves with linear velocity $v$ along a circular path of radius $r$ , the linear velocity is related to the angular velocity by:

$v = \omega r$

Example:

Suppose an object completes a 4π radian rotation (two full circles) in 4 seconds. Its angular velocity is:

$\omega = \frac{4\pi}{4} = \pi \text{ rad/s}$

If the radius of the path is 2 meters, then the linear velocity $v$ is:

$v = \pi \times 2 = 2\pi \approx 6.28 \text{ m/s}$

Angular Acceleration

Angular acceleration ( $\alpha$ ) is the rate of change of angular velocity over time. It represents how quickly the angular velocity of an object changes, particularly in non-uniform circular motion where the object speeds up or slows down as it travels the circular path.

Formula:

$\alpha = \frac{\Delta \omega}{\Delta t}$

where:

$\alpha$ is the angular acceleration,
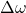$\Delta \omega$ is the change in angular velocity, and
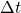$\Delta t$ is the time over which the change occurs.

Example:

If an object’s angular velocity increases from 2 rad/s to 6 rad/s over 4 seconds, the angular acceleration is:

$\alpha = \frac{6 - 2}{4} = \frac{4}{4} = 1 \text{ rad/s}^2$

Centripetal Acceleration

For an object in circular motion, centripetal acceleration is the acceleration directed towards the center of the circular path. This inward-directed acceleration keeps the object moving in a curved path rather than in a straight line. Centripetal acceleration depends on both the speed of the object and the radius of the circular path.

Formula:

$a_c = \frac{v^2}{r}$

or, using angular velocity $\omega$ ,

$a_c = \omega^2 r$

where:

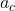$a_c$ is the centripetal acceleration,
$v$ is the linear velocity, and
$r$ is the radius of the circular path.

Example:

If a car is traveling at a speed of 20 m/s along a curve with a radius of 50 meters, its centripetal acceleration is:

$a_c = \frac{20^2}{50} = \frac{400}{50} = 8 \text{ m/s}^2$

This acceleration is directed toward the center of the curve and is necessary for the car to continue following the circular path.

Centripetal Force

Centripetal force is the force required to keep an object moving in a circular path, and it acts perpendicular to the direction of motion, pointing toward the center of the circle. This force is responsible for maintaining the object’s circular trajectory.

Formula:

$F_c = m a_c$

$F_c = \frac{m v^2}{r} = m \omega^2 r$

where:

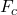$F_c$ is the centripetal force,
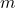$m$ is the mass of the object,
$v$ is the linear velocity, and
$r$ is the radius of the circular path.

Example:

If a 1,000 kg car is traveling at 20 m/s around a curve with a radius of 50 meters, the centripetal force required to keep it on the curve is:

$F_c = \frac{1000 \times 20^2}{50} = \frac{1000 \times 400}{50} = 8000 \text{ N}$

Real-Life Examples of Circular Motion

1. Car on a Curved Road

When a car makes a turn, it undergoes circular motion, and the friction between the tires and the road provides the centripetal force needed to keep the car on its path. If the car speeds up, the centripetal force requirement increases; thus, sharper turns or higher speeds can lead to skidding if friction is insufficient.

Example:

A car traveling at 30 m/s around a bend with a radius of 100 meters experiences centripetal acceleration:

$a_c = \frac{30^2}{100} = 9 \text{ m/s}^2$

To maintain this turn, the frictional force must meet the centripetal force requirement.

2. Roller Coaster Loop

In a roller coaster, as the cart moves through a vertical loop, it experiences circular motion. At the top of the loop, both gravity and the normal force from the track provide the centripetal force needed to keep the cart in motion. This combination of forces ensures the cart stays on the track even when upside down.

Example:

If the cart’s speed at the top of a loop with a 10-meter radius is 10 m/s, the centripetal force needed is:

$F_c = \frac{m \times 10^2}{10} = 10m$

The gravitational force $(mg)$ contributes to this centripetal force, allowing the cart to complete the loop.

3. Planetary Motion

Planets orbit the Sun in a nearly circular path due to the gravitational force exerted by the Sun, which acts as a centripetal force. This force keeps the planets in orbit, preventing them from moving in a straight line away from the Sun.

Example:

For Earth, with an orbital radius of approximately $1.5 \times 10^{11}$ meters and an orbital speed of about $3 \times 10^4$ m/s, the centripetal force exerted by the Sun’s gravity is essential to maintain this orbit.

Conclusion

The kinematics of circular motion provides a comprehensive understanding of the motion of objects that follow curved paths. From calculating angular velocity and centripetal acceleration to understanding the centripetal force needed to sustain circular motion, these concepts have widespread applications in real-world situations, such as vehicle dynamics, planetary orbits, and amusement park rides. Mastering the equations and principles of circular motion allows for a deeper understanding of how forces and accelerations govern objects moving in circular paths, ultimately enhancing our ability to design and interpret circular motion in natural and engineered systems.