Arus bolak-balik (AC) digunakan dalam berbagai sistem kelistrikan. Artikel ini membahas konsep dasar AC, persamaannya, serta contoh penerapannya dalam kehidupan sehari-hari.
Pendahuluan
Arus listrik adalah aliran muatan listrik yang bergerak melalui suatu penghantar. Secara umum, arus listrik terbagi menjadi dua jenis utama, yaitu arus searah (DC – Direct Current) dan arus bolak-balik (AC – Alternating Current).
Arus searah (DC) memiliki arah aliran yang tetap, seperti yang ditemukan pada baterai. Sementara itu, arus bolak-balik (AC) memiliki arah yang berubah-ubah secara periodik. Sebagian besar sistem kelistrikan di dunia, termasuk listrik rumah tangga dan jaringan transmisi tenaga listrik, menggunakan arus bolak-balik karena lebih efisien dalam distribusi energi listrik jarak jauh.
Artikel ini akan menjelaskan konsep dasar arus bolak-balik, bagaimana ia bekerja, serta persamaan matematis yang digunakan untuk menganalisisnya.
- —
Apa Itu Arus Bolak-Balik (AC)?
Arus bolak-balik (AC) adalah jenis arus listrik yang berubah arah secara periodik. Dalam satu siklus, arus AC akan mengalir dalam satu arah, mencapai nilai maksimum, kembali ke nol, lalu mengalir dalam arah berlawanan sebelum kembali ke nol lagi.
Bentuk gelombang AC yang paling umum adalah gelombang sinusoidal, di mana perubahan arus dan tegangan terjadi secara halus dan periodik.
Dalam sistem listrik rumah tangga, arus AC biasanya memiliki frekuensi 50 Hz atau 60 Hz, tergantung pada standar negara masing-masing. Ini berarti dalam satu detik, arus AC berubah arah sebanyak 50 atau 60 kali.
Contoh: Listrik Rumah Tangga
Di sebagian besar negara, listrik yang masuk ke rumah memiliki tegangan 220 V dengan frekuensi 50 Hz. Ini berarti dalam satu detik, arus listrik berbalik arah sebanyak 50 kali. Jika diamati menggunakan osiloskop, bentuk gelombangnya akan menyerupai pola sinusoidal yang berulang.
- —
Persamaan Matematis Arus Bolak-Balik
Karena arus AC memiliki perubahan arah dan besar secara periodik, kita dapat merepresentasikan arus dan tegangan dengan persamaan fungsi sinus atau kosinus.
1. Persamaan Tegangan dan Arus AC
Tegangan dalam arus bolak-balik dapat dituliskan sebagai:
![]()
Sedangkan arus dalam rangkaian AC dapat dinyatakan sebagai:
![]()
di mana:
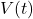 dan
dan 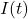 adalah tegangan dan arus sebagai fungsi waktu,
adalah tegangan dan arus sebagai fungsi waktu,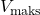 dan
dan 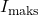 adalah nilai puncak tegangan dan arus,
adalah nilai puncak tegangan dan arus,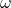 adalah frekuensi sudut (
adalah frekuensi sudut (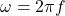 , dengan
, dengan 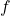 sebagai frekuensi dalam Hertz),
sebagai frekuensi dalam Hertz),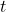 adalah waktu dalam detik,
adalah waktu dalam detik,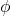 adalah sudut fase antara arus dan tegangan.
adalah sudut fase antara arus dan tegangan.
Contoh Perhitungan Tegangan AC
Misalkan tegangan maksimum pada suatu rangkaian AC adalah 311 V, dengan frekuensi 50 Hz. Persamaan tegangan dapat dituliskan sebagai:
![]()
Jika kita ingin mengetahui tegangan pada waktu ![]() milidetik (0,005 s), maka:
milidetik (0,005 s), maka:
![]()
![]()
![]()
Ini menunjukkan bahwa pada saat ![]() milidetik, tegangan mencapai nilai maksimum.
milidetik, tegangan mencapai nilai maksimum.
- —
Nilai Efektif (RMS) dalam Arus AC
Karena arus dan tegangan AC terus berubah dari waktu ke waktu, penting untuk menggunakan nilai efektif (RMS – Root Mean Square) untuk menghitung daya dan melakukan perhitungan praktis.
Persamaan Nilai RMS
![]()
![]()
Nilai RMS ini merupakan nilai setara dengan arus atau tegangan DC yang menghasilkan daya yang sama dalam rangkaian.
Contoh Perhitungan Nilai RMS
Misalkan tegangan maksimum dalam jaringan listrik rumah adalah 311 V. Maka nilai RMS-nya:
![]()
Inilah sebabnya mengapa tegangan listrik di rumah disebut 220 V, meskipun nilai puncaknya sebenarnya lebih besar.
- —
Fase dalam Rangkaian AC
Dalam sistem AC, arus dan tegangan tidak selalu berada dalam fase yang sama. Perbedaan fase ini disebabkan oleh induktor (L) dan kapasitor (C) dalam rangkaian.
- Dalam rangkaian resistif murni, arus dan tegangan berada dalam fase yang sama (
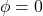 ).
). - Dalam rangkaian induktif, arus tertinggal 90° terhadap tegangan (
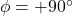 ).
). - Dalam rangkaian kapasitif, arus mendahului tegangan sebesar 90° (
 ).
).
Contoh Perhitungan Sudut Fase
Jika sebuah rangkaian memiliki impedansi dengan komponen resistif sebesar 10 Ω dan reaktansi induktif sebesar 10 Ω, maka sudut fase dapat dihitung sebagai:
![]()
![]()
Ini berarti arus tertinggal tegangan sebesar 45°.
- —
Penerapan Arus Bolak-Balik dalam Kehidupan Sehari-hari
1. Jaringan Listrik Rumah Tangga
Semua perangkat listrik rumah seperti lampu, televisi, dan kulkas menggunakan arus AC dari PLN dengan frekuensi 50 Hz.
2. Transformator
Transformator digunakan untuk menaikkan atau menurunkan tegangan AC dalam distribusi tenaga listrik, memungkinkan listrik dikirim dengan efisien dari pembangkit ke konsumen.
3. Motor Listrik AC
Banyak peralatan industri menggunakan motor AC, seperti kipas angin, mesin pendingin, dan alat-alat berat lainnya.
- —
Kesimpulan
Arus bolak-balik (AC) adalah jenis arus listrik yang berubah arah secara periodik dan digunakan dalam sistem kelistrikan global. Konsep dasar AC melibatkan persamaan matematis untuk menentukan tegangan, arus, impedansi, dan daya.
Nilai RMS digunakan untuk menyatakan tegangan dan arus AC dalam bentuk yang lebih praktis, sementara sudut fase menentukan hubungan antara arus dan tegangan dalam rangkaian yang mengandung resistor, induktor, dan kapasitor.
Dengan memahami konsep dasar dan persamaannya, kita dapat lebih memahami bagaimana listrik bekerja dalam kehidupan sehari-hari serta bagaimana merancang sistem kelistrikan yang efisien dan aman.