Linear momentum is one of the most fundamental concepts in physics, playing a central role in understanding the movement of objects and the interactions between them. Momentum refers to the quantity of motion that an object possesses and is directly related to both the mass of the object and its velocity. Linear momentum helps explain a wide range of physical phenomena, from the collision of vehicles to the motion of planets in space. It also plays a crucial role in fields such as engineering, sports science, and astronomy.

This article will explore the concept of linear momentum in detail, discussing its definition, principles, conservation laws, and real-world examples that illustrate its importance in understanding the dynamics of moving objects.
What is Linear Momentum?
Linear momentum, often simply referred to as momentum, is a vector quantity that measures the motion of an object. It is defined as the product of an object’s mass and its velocity:
p=mv
Where:
- p is the linear momentum,
- m is the mass of the object,
- v is the velocity of the object.
Because velocity is a vector (having both magnitude and direction), momentum is also a vector, meaning that it has both a direction and a magnitude. The direction of the momentum is the same as the direction of the object’s velocity, and its magnitude depends on both the speed of the object and its mass.
Key Characteristics of Linear Momentum:
- Magnitude: The magnitude of momentum increases with both the mass of the object and its speed. This means that heavier and faster-moving objects have more momentum.
- Direction: The momentum vector points in the same direction as the object’s velocity.
- Units: In the SI system, linear momentum is measured in kilogram meters per second (kg·m/s).
Example of Linear Momentum:
Imagine a car moving along a straight road at 60 km/h. If the car’s mass is 1,000 kg, its linear momentum is calculated as follows:
p=mv=(1,000kg)(60km/h)=1,000×16.67m/s=16,670kg.m/s
Thus, the car’s momentum is 16,670 kg·m/s in the direction of its motion. This momentum is significant because it reflects how difficult it would be to stop the car or change its direction.
Principles of Linear Momentum
Linear momentum is governed by several important principles that explain how it behaves during different types of interactions, such as collisions, external forces, and explosions.
1. Conservation of Linear Momentum
One of the most fundamental laws of physics is the law of conservation of linear momentum, which states that the total momentum of a closed system (one without external forces) remains constant if no external forces act upon it. In other words, the total momentum before an interaction (such as a collision) is equal to the total momentum after the interaction.
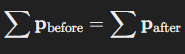
This principle applies to a wide range of phenomena, from the collision of objects to the recoil of a gun. It also underpins much of classical mechanics and is crucial in the study of both isolated systems and systems under various forces.
Example: Collision of Two Objects
Consider two ice skaters gliding towards each other. Skater A has a mass of 70 kg and is moving with a velocity of 3 m/s to the right, while skater B has a mass of 60 kg and is moving with a velocity of 2 m/s to the left. Before they collide, their total momentum is:
If no external forces are acting on them, the total momentum after the collision must also be 90 kg·m/s, although how this momentum is distributed between the two skaters depends on the nature of the collision.
2. Impulse and Momentum
Impulse is related to momentum in that it measures the change in momentum caused by a force acting over a period of time. The impulse-momentum theorem states that the impulse on an object is equal to the change in its momentum:
J=Δp=mΔv
Where:
- J is the impulse,
- Δp is the change in momentum,
- m is the mass,
- Δv is the change in velocity.
Impulse is calculated as the product of the force applied and the time for which it is applied:
J=FΔt
Impulse explains why applying a small force over a longer period can have the same effect as applying a large force over a shorter period.
Example: Car Crashes and Airbags
In the case of a car crash, the momentum of the moving car must change to zero as the car comes to a stop. If the stop happens suddenly (such as hitting a wall), the force on the driver can be very large. However, if airbags are used, they increase the time over which the car’s momentum is brought to zero, thereby reducing the force experienced by the driver. This illustrates the relationship between impulse and momentum, as the airbags reduce the peak force by increasing the duration of the impact.
3. Elastic and Inelastic Collisions
When two objects collide, they can either bounce off each other or stick together. The type of collision determines how kinetic energy and momentum behave during the interaction.
Elastic Collisions
In an elastic collision, both momentum and kinetic energy are conserved. This means that after the collision, the total momentum and the total kinetic energy of the system remain the same as before the collision. Elastic collisions typically occur between hard, bouncy objects, such as billiard balls.
Inelastic Collisions
In an inelastic collision, momentum is conserved, but kinetic energy is not. Some of the kinetic energy is transformed into other forms of energy, such as heat, sound, or deformation. A perfectly inelastic collision occurs when the colliding objects stick together and move as a single object after the collision.
Example: Elastic Collision in Pool
When two billiard balls collide on a pool table, the collision is nearly elastic, meaning the balls rebound with little loss of kinetic energy. The total momentum of the two balls before the collision is equal to the total momentum after the collision, but each ball’s velocity may change depending on their masses and initial velocities.
Example: Inelastic Collision in Football
In a football game, when two players collide and tackle each other, the collision is often inelastic. The players may hold onto each other and fall to the ground together, meaning they move as one object after the collision. Although momentum is conserved, some of the kinetic energy is lost to heat, sound, and deformation (e.g., pads compressing or bodies bending).
The Relationship Between Linear Momentum and Force
Newton’s second law of motion provides a direct link between force and momentum. It states that the net force acting on an object is equal to the rate of change of its momentum over time:
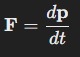
In the case of constant mass, this simplifies to:
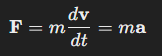
Thus, force is equal to mass times acceleration, where acceleration is the rate of change of velocity. The second law highlights that a force is required to change the momentum of an object, either by changing its velocity (speed or direction) or its mass (though the latter is rare in everyday situations).
Example: Rocket Propulsion
In rocket propulsion, momentum is conserved, but the rocket’s mass changes as it burns fuel. As the rocket expels gas at high velocity, the rocket gains momentum in the opposite direction (due to conservation of momentum), which accelerates the rocket forward. This principle is central to space travel, where rockets must carry fuel to create thrust in the vacuum of space.
Angular Momentum vs. Linear Momentum
While linear momentum deals with objects moving in straight lines, angular momentum refers to objects that are rotating or spinning around an axis. Just as linear momentum is conserved in straight-line motion, angular momentum is conserved in rotational motion.
Angular momentum is given by:
L=r×p
Where:
- L is the angular momentum,
- r is the position vector (the distance from the axis of rotation),
- p is the linear momentum,
- × represents the cross product.
Angular momentum plays a crucial role in systems such as rotating planets, figure skaters performing spins, and even the movement of electrons around atomic nuclei.
Example: Ice Skater’s Spin
When an ice skater pulls in their arms while spinning, they reduce their moment of inertia, causing their angular velocity to increase. This is an example of conservation of angular momentum. The skater’s angular momentum remains constant, but by pulling in their arms, they decrease their rotational inertia, which leads to a faster spin.
Real-World Applications of Linear Momentum
Linear momentum has countless real-world applications that affect daily life, engineering, and technology. Here are a few examples:
1. Sports
In sports like soccer, baseball, and basketball, momentum plays a key role in determining how objects move and interact. For instance, when a soccer player kicks a ball, they transfer their momentum to the ball, causing it to accelerate toward the goal. The harder the kick, the greater the force and momentum imparted to the ball.
2. Vehicle Collisions
In vehicle safety, momentum and the conservation of momentum are used to analyze the severity of crashes and design safety features like seatbelts, airbags, and crumple zones. These features are designed to absorb and dissipate energy, reducing the impact force and protecting passengers.
3. Space Exploration
In space exploration, rockets rely on the principle of conservation of momentum to propel themselves into space. As fuel is ejected at high speed from the rocket’s engines, the rocket gains momentum in the opposite direction, allowing it to overcome Earth’s gravity and reach orbit.
Conclusion
Linear momentum is a fundamental concept in physics that describes the motion of objects and how they interact with forces. It is a conserved quantity in isolated systems, meaning that the total momentum before and after an event, such as a collision, remains constant. The principle of momentum conservation is crucial for understanding a wide range of phenomena, from simple collisions in sports to complex rocket propulsion in space.
Through principles like impulse, elastic and inelastic collisions, and the relationship between momentum and force, linear momentum provides a comprehensive framework for analyzing motion and impact. Its real-world applications are vast, impacting industries as diverse as vehicle safety, sports, and space exploration, making it one of the cornerstones of classical mechanics.