Menghitung Arus, Tegangan, Impedansi, dan Daya dalam Rangkaian AC

Pelajari cara menghitung arus, tegangan, impedansi, dan daya dalam rangkaian AC. Artikel ini menjelaskan konsep dan rumus dengan contoh nyata untuk pemahaman yang lebih mudah.

Pendahuluan

Arus bolak-balik (AC) adalah jenis arus listrik yang digunakan dalam sebagian besar sistem kelistrikan di rumah, industri, dan jaringan tenaga listrik. Berbeda dengan arus searah (DC) yang memiliki arah tetap, arus AC berubah arah secara periodik.

Dalam rangkaian AC, perhitungan arus, tegangan, impedansi, dan daya menjadi lebih kompleks karena adanya elemen tambahan seperti kapasitansi (C) dan induktansi (L) yang menyebabkan perubahan fase antara arus dan tegangan. Oleh karena itu, pemahaman mengenai cara menghitung parameter-parameter ini sangat penting dalam analisis rangkaian AC.

Artikel ini akan menjelaskan bagaimana menghitung arus, tegangan, impedansi, dan daya dalam rangkaian AC dengan contoh konkret untuk memperjelas setiap konsep.

Menghitung Arus dalam Rangkaian AC

Dalam rangkaian AC, arus dapat dinyatakan dalam bentuk arus efektif (RMS – Root Mean Square) atau dalam bentuk fasor yang merepresentasikan besar dan sudut fase arus. Arus dalam suatu rangkaian AC dapat dihitung menggunakan hukum Ohm dalam bentuk impedansi:

$I = \frac{V}{Z}$

di mana:

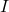$I$ adalah arus dalam ampere (A),
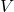$V$ adalah tegangan dalam volt (V),
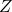$Z$ adalah impedansi dalam ohm (Ω).

Contoh Perhitungan Arus dalam Rangkaian Resistor Murni

Misalkan sebuah rangkaian AC memiliki tegangan 220 V dengan beban resistif 50 Ω. Maka, arus dalam rangkaian adalah:

$I = \frac{220}{50} = 4.4 A$

Karena hanya ada resistor, arus dan tegangan berada dalam fase yang sama, yang berarti tidak ada perbedaan sudut fase.

Contoh Perhitungan Arus dalam Rangkaian Induktif

Jika rangkaian memiliki induktor dengan reaktansi induktif $X_L = 30 \Omega$ dan resistor $R = 40 \Omega$ , maka impedansi totalnya dihitung sebagai:

$Z = \sqrt{R^2 + X_L^2} = \sqrt{40^2 + 30^2} = \sqrt{1600 + 900} = \sqrt{2500} = 50 \Omega$

Jika tegangan tetap 220 V, maka arusnya:

$I = \frac{220}{50} = 4.4 A$

Namun, karena ada induktor, arus akan tertinggal 90° terhadap tegangan.

Menghitung Tegangan dalam Rangkaian AC

Tegangan dalam rangkaian AC seringkali bergantung pada jenis komponen dalam rangkaian, seperti resistor (R), induktor (L), dan kapasitor (C). Dalam banyak kasus, kita menggunakan hukum Kirchhoff atau hukum Ohm untuk menentukan tegangan.

Jika diketahui arus dalam rangkaian, tegangan pada setiap komponen dapat dihitung sebagai berikut:

Resistor: $V_R = I R$
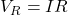
Induktor: 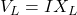$V_L = I X_L$ , di mana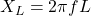 $X_L = 2\pi f L$
Kapasitor: 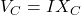$V_C = I X_C$ , di mana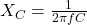 $X_C = \frac{1}{2\pi f C}$

Contoh Perhitungan Tegangan dalam Rangkaian RLC Seri

Misalkan sebuah rangkaian seri terdiri dari:

Resistor 10 Ω,
Induktor dengan reaktansi induktif 20 Ω,
Kapasitor dengan reaktansi kapasitif 30 Ω,
Tegangan sumber 120 V.

Impedansi total:

$Z = \sqrt{R^2 + (X_L - X_C)^2} = \sqrt{10^2 + (20 - 30)^2} = \sqrt{10^2 + (-10)^2} = \sqrt{100 + 100} = 14.14 \Omega$

Arus dalam rangkaian:

$I = \frac{120}{14.14} = 8.49 A$

Maka tegangan pada masing-masing komponen adalah:

$V_R = (8.49)(10) = 84.9 V$

$V_L = (8.49)(20) = 169.8 V$

$V_C = (8.49)(30) = 254.7 V$

Menghitung Impedansi dalam Rangkaian AC

Impedansi ( $Z$ ) dalam rangkaian AC merupakan gabungan dari resistansi dan reaktansi (induktif dan kapasitif).

Rumus impedansi dalam rangkaian seri:

$Z = \sqrt{R^2 + (X_L - X_C)^2}$

Rumus impedansi dalam rangkaian paralel:

$\frac{1}{Z} = \sqrt{\frac{1}{R^2} + \left(\frac{1}{X_L} - \frac{1}{X_C}\right)^2}$

Contoh Perhitungan Impedansi dalam Rangkaian Kapasitif Murni

Misalkan ada kapasitor dengan kapasitansi 100 µF pada frekuensi 50 Hz. Reaktansi kapasitifnya:

$X_C = \frac{1}{2\pi f C} = \frac{1}{2\pi (50)(100 \times 10^{-6})} = \frac{1}{0.0314} = 31.8 \Omega$

Karena tidak ada resistor atau induktor, impedansi total adalah 31.8 Ω.

Menghitung Daya dalam Rangkaian AC

Daya dalam rangkaian AC tidak hanya bergantung pada tegangan dan arus, tetapi juga pada faktor daya ( $\cos \theta$ ).

Ada tiga jenis daya dalam rangkaian AC:

1. Daya Aktif (P) – daya yang benar-benar digunakan:

$P = VI \cos \theta$

2. Daya Reaktif (Q) – daya yang tersimpan dalam medan listrik/magnet:

$Q = VI \sin \theta$

3. Daya Semu (S) – kombinasi daya aktif dan daya reaktif:

$S = VI$

Contoh Perhitungan Daya dalam Rangkaian AC

Misalkan dalam suatu rangkaian AC, diketahui:

Tegangan 230 V
Arus 10 A
Faktor daya 0.8

Maka:

Daya Aktif:

$P = 230 \times 10 \times 0.8 = 1840 W$

Daya Reaktif:

$Q = 230 \times 10 \times \sin (\cos^{-1} 0.8) = 1380 VAR$

Daya Semu:

$S = 230 \times 10 = 2300 VA$

Kesimpulan

Menghitung arus, tegangan, impedansi, dan daya dalam rangkaian AC memerlukan pemahaman tentang hukum Ohm, hukum Kirchhoff, dan konsep fasor. Dengan memahami rumus-rumus dasar serta aplikasinya dalam kehidupan nyata, kita dapat menganalisis dan mendesain sistem kelistrikan dengan lebih efektif.

Pemahaman ini sangat penting dalam bidang teknik listrik, elektronika, dan industri tenaga listrik untuk memastikan sistem bekerja secara optimal dan efisien.