Motion Parameters: Understanding the Fundamentals of Movement in Physics

Motion is one of the most fundamental concepts in physics, describing the change in the position of an object over time. It is a concept that we encounter in our everyday lives, from a car driving down a road to the planets orbiting around the sun. The study of motion involves understanding several key parameters that describe how objects move, the forces involved, and the patterns of movement. These parameters include displacement, velocity, acceleration, time, and distance.

In this article, we will explore the various motion parameters in detail, their significance in understanding different types of motion, and provide examples to illustrate how these parameters work in real-life situations.

1. Displacement and Distance

Displacement and distance are two fundamental terms in motion, often confused but distinctly different.

Displacement

Displacement refers to the shortest straight-line distance between an object’s initial and final positions, considering the direction of movement. It is a vector quantity, meaning it has both magnitude and direction. Displacement is concerned with where the object is relative to its starting point, not the total path it traveled.

Formula for Displacement:

Displacement=Δx=x_f−x_i

Where:

Δx is the displacement,
x_f is the final position,
x_i is the initial position.

Example: If a person walks 4 km east, then 3 km west, the total distance traveled is 7 km, but the displacement is only 1 km east, as displacement focuses on the net change in position, not the path taken.

Distance

Distance, on the other hand, is the total length of the path traveled by an object, without considering direction. It is a scalar quantity, which means it only has magnitude (no direction). Distance represents the complete ground covered during motion.

Example: Using the same example, walking 4 km east and 3 km west results in a total distance of 7 km, but displacement is only 1 km eastward. While the distance traveled considers every step, displacement focuses on the difference between the starting and ending points.

2. Velocity and Speed

Velocity and speed are often thought of as interchangeable, but they describe different aspects of motion. Understanding both is critical for describing how fast an object moves and in which direction.

Velocity

Velocity is the rate of change of displacement over time and is a vector quantity, meaning it involves both magnitude (how fast) and direction (where). Velocity tells us how quickly an object changes its position and the direction in which it is moving.

Formula for Velocity:

Where:

Δx is the displacement,
Δt is the time interval.

Example: If a car moves 100 meters east in 10 seconds, the velocity of the car is:

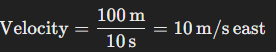
n this case, velocity gives both the speed (10 m/s) and the direction (east).

Speed

Speed is the rate at which an object covers distance and is a scalar quantity, meaning it only concerns magnitude, not direction. Speed measures how fast something moves regardless of where it is going.

Formula for Speed:

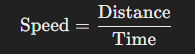
Example: If a person walks a total distance of 500 meters in 5 minutes, their average speed would be:

Unlike velocity, speed only tells us how fast the person is moving without regard to the direction.

Difference Between Velocity and Speed

Velocity considers the direction of motion and the net displacement.
Speed only measures how fast an object moves, irrespective of direction.

For instance, a person walking in a circular path back to the starting point may have covered a large distance, resulting in a high speed, but their displacement would be zero, yielding a velocity of zero.

3. Acceleration

Acceleration refers to the rate of change of velocity over time. It is a vector quantity, meaning it has both magnitude and direction. Acceleration occurs whenever an object’s velocity changes—whether that change involves speeding up, slowing down, or changing direction.

Formula for Acceleration

Where:

Δv is the change in velocity,
Δt is the time interval over which the change occurs.

Types of Acceleration

Positive Acceleration: When an object speeds up, its velocity increases, resulting in positive acceleration. For example, a car accelerating from 0 to 60 mph experiences positive acceleration.
Negative Acceleration (Deceleration): When an object slows down, its velocity decreases, resulting in negative acceleration. For example, a car coming to a stop from 60 mph experiences deceleration.
Uniform Acceleration: Occurs when an object’s velocity changes by a constant amount over equal time intervals. Free-falling objects under gravity (ignoring air resistance) are an example, where acceleration remains constant at 9.8 m/s².
Non-uniform Acceleration: When the rate of velocity change is not constant, such as a car accelerating at varying speeds.

Example of Acceleration

If a car increases its velocity from 20 m/s to 30 m/s in 5 seconds, the acceleration can be calculated as:

This means the car’s velocity is increasing by 2 meters per second every second.

4. Time

Time is one of the essential parameters in motion, representing the interval during which an event occurs. In the context of motion, time helps determine how long it takes for an object to move from one position to another or how long it takes for an object to accelerate to a certain speed.

In all motion equations, time ( $t$ ) plays a crucial role, linking displacement, velocity, and acceleration. Understanding the time taken for events to occur is fundamental in calculating other motion parameters.

Example of Time in Motion

If a ball rolls down a hill and travels 100 meters in 20 seconds, the time parameter helps us calculate speed or velocity. In this case, the speed would be:

5. Equations of Motion

In physics, there are three primary equations of motion that relate displacement, velocity, acceleration, and time for objects moving with uniform acceleration. These equations help describe the motion of objects under various conditions and are used widely in solving motion problems.

First Equation of Motion

v=u+at

Where:

v is the final velocity,
u is the initial velocity,
a is the acceleration,
t is the time.

Example:

A car starts from rest ( $u = 0$ ) and accelerates at a rate of 2 m/s² for 5 seconds. The final velocity of the car can be calculated as:

v=0+(2×5)=10m/s

Second Equation of Motion

Where:

s is the displacement,
u is the initial velocity,
a is the acceleration,
t is the time.

Example:

Using the same car example, if the car starts from rest (u=0u = 0), accelerates at 2 m/s² for 5 seconds, the displacement of the car is:

Third Equation of Motion

v²=u²+2as

Where:

v is the final velocity,
u is the initial velocity,
a is the acceleration,
s is the displacement.

Example:

If a car accelerates at 2 m/s² over a distance of 50 meters starting from rest, the final velocity can be calculated using:

v²=0²+2(2)(50)=200

Taking the square root of both sides:

v=√200=14.14 m/s

Conclusion

Motion parameters such as displacement, velocity, acceleration, time, and distance form the foundation for understanding movement in physics. By analyzing these parameters, we can describe and predict the motion of objects, whether they are cars on a highway, balls rolling down a hill, or planets moving through space.

Each parameter plays a unique role, and the relationships between them are governed by the equations of motion. Understanding these concepts is essential not only for solving physics problems but also for grasping how objects move and interact in the real world. From the motion of athletes to the functioning of machines, motion parameters offer the tools we need to describe, analyze, and appreciate the physical world.