Motion Under Gravity: Understanding Free Fall and Projectile Motion

Motion under gravity refers to the movement of objects influenced solely by the gravitational force, which acts as a constant acceleration towards the Earth’s surface. This type of motion is ubiquitous in everyday life and is crucial for understanding physical phenomena, from falling objects to the trajectory of a basketball shot. Gravity imparts a uniform acceleration, denoted as $g$ , with an approximate value of $9.8 \, \text{m/s}^2$ near the Earth’s surface.

This article delves into the principles governing motion under gravity, the equations of motion, and practical examples, providing a comprehensive understanding of how objects behave in free fall and projectile motion.

Key Concepts of Motion Under Gravity

1. Gravitational Acceleration

Gravitational acceleration ( $g$ ) is the rate at which an object’s velocity changes due to gravity. Regardless of an object’s mass, it experiences the same acceleration under gravity in the absence of air resistance. This principle, first demonstrated by Galileo, highlights the universality of gravity’s effect on all objects.

2. Free Fall

Free fall is a special case of motion under gravity where the only force acting on an object is gravitational force. Air resistance is typically neglected in these scenarios. In free fall:

The initial velocity ( 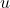$u$ ) is often zero if the object is dropped from rest.
The object accelerates uniformly at $g$ .
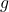Its motion can be described using kinematic equations.

Example of Free Fall

A stone is dropped from a height of $20 \, \text{m}$ . How long does it take to hit the ground?

Using the equation:

$s = ut + \frac{1}{2} g t^2$

Here, $s = 20 \, \text{m}, u = 0, g = 9.8 \, \text{m/s}^2$ :

$20 = 0 + \frac{1}{2} (9.8) t^2$

$20 = 4.9 t^2$

$t^2 = \frac{20}{4.9} \approx 4.08$

$t \approx 2.02 \, \text{seconds.}$

Thus, the stone takes approximately $2.02 \, \text{s}$ to reach the ground.

3. Projectile Motion

When an object is launched into the air, it follows a curved path called a projectile trajectory due to the influence of gravity. This motion has two components:

Horizontal motion: Constant velocity ( 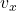$v_x$ ) because no horizontal force acts (ignoring air resistance).
Vertical motion: Uniform acceleration due to gravity.

The combination of these motions forms a parabolic trajectory.

Example of Projectile Motion

A ball is thrown horizontally with a velocity of $10 \, \text{m/s}$ from a height of $15 \, \text{m}$ . How far does it travel horizontally before hitting the ground?

First, calculate the time of flight using the vertical motion equation:

$s = \frac{1}{2} g t^2$

$15 = \frac{1}{2} (9.8) t^2$

$t^2 = \frac{15}{4.9} \approx 3.06$

$t \approx 1.75 \, \text{s.}$

Next, calculate horizontal displacement:

$x = v_x t = 10 \times 1.75 = 17.5 \, \text{m.}$

The ball travels $17.5 \, \text{m}$ horizontally before hitting the ground.

Equations of Motion Under Gravity

Motion under gravity is governed by the equations of motion, which can be applied to both free fall and projectile motion:

1. Displacement:

$s = ut + \frac{1}{2} g t^2$

2. Final Velocity:

$v = u + g t$

3. Velocity-Displacement Relationship:

$v^2 = u^2 + 2 g s$

Here:

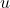$u$ = initial velocity,
$v$ = final velocity,
$s$ = displacement,
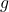$g$ = acceleration due to gravity,
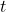$t$ = time.

Real-World Examples of Motion Under Gravity

1. Dropping an Object from a Height

A coin dropped from a building represents free fall. Ignoring air resistance, the coin accelerates uniformly at $g$ . The equations of motion can predict its time to reach the ground and its velocity upon impact.

Problem:

A coin is dropped from a height of $80 \, \text{m}$ . Find its velocity upon hitting the ground.

Using:

$v^2 = u^2 + 2 g s$

Here, $u = 0, g = 9.8 \, \text{m/s}^2, s = 80 \, \text{m}$ :

$v^2 = 0 + 2 (9.8) (80)$

$v^2 = 1568$

$v = \sqrt{1568} \approx 39.6 \, \text{m/s.}$

Thus, the coin strikes the ground with a velocity of approximately $39.6 \, \text{m/s}$ .

2. Throwing an Object Upward

When an object is thrown upward, its velocity decreases due to gravity until it reaches a peak (velocity = 0), after which it begins to fall back down.

Problem:

A ball is thrown vertically upward with an initial velocity of $20 \, \text{m/s}$ . How high does it go?

Using:

$v^2 = u^2 - 2 g h$

Here, $v = 0, u = 20 \, \text{m/s}, g = 9.8 \, \text{m/s}^2$ :

$0 = 20^2 - 2 (9.8) h$

$400 = 19.6 h$

$h = \frac{400}{19.6} \approx 20.41 \, \text{m.}$

The ball reaches a maximum height of approximately $20.41 \, \text{m}$ .

3. Projectile Motion in Sports

In sports like basketball or football, understanding projectile motion helps athletes optimize their shots or kicks.

Problem:

A basketball player shoots the ball at a velocity of $12 \, \text{m/s}$ at an angle of $45^\circ$ . How far does the ball travel horizontally?

First, resolve the initial velocity into components:

$v_x = 12 \cos 45^\circ = 12 \times \frac{\sqrt{2}}{2} = 8.49 \, \text{m/s}$

$v_y = 12 \sin 45^\circ = 12 \times \frac{\sqrt{2}}{2} = 8.49 \, \text{m/s.}$

Time of flight:

$t = \frac{2 v_y}{g} = \frac{2 (8.49)}{9.8} \approx 1.73 \, \text{s.}$

Horizontal range:

$x = v_x \times t = 8.49 \times 1.73 \approx 14.68 \, \text{m.}$

The ball travels approximately $14.68 \, \text{m}$ .

Applications of Motion Under Gravity

1. Engineering and Construction

Understanding motion under gravity helps engineers design structures, predict falling object behavior, and ensure safety. For example, engineers calculate the trajectory of debris during controlled demolitions.

2. Space Exploration

The principles of motion under gravity guide spacecraft launches and satellite positioning. For instance, calculating the escape velocity ensures that rockets overcome Earth’s gravitational pull.

3. Sports and Recreation

In sports, players and coaches use gravity-based motion to perfect techniques like free throws in basketball or javelin throws.

Conclusion

Motion under gravity is a fundamental aspect of physics that governs a wide range of natural and man-made phenomena. By mastering the principles of free fall and projectile motion, along with the equations of motion, we can predict and analyze the behavior of objects in various scenarios. From dropping objects to launching rockets, the study of motion under gravity provides critical insights into the workings of our physical world.