The parametric equation of a circle provides a way to describe every point on the circle in terms of a variable, known as the parameter. This approach to representing a circle is powerful because it allows us to define each point on the circle using trigonometric functions, enabling a smooth and continuous representation. Parametric equations of circles are used extensively in physics, engineering, and computer graphics for tasks involving circular motion and rotations.
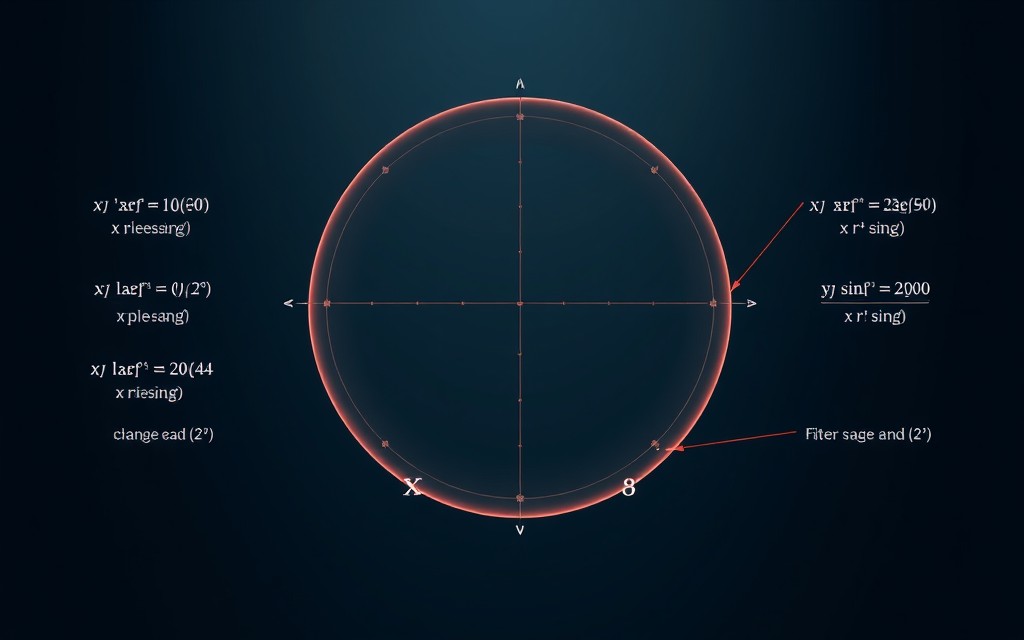
In this article, we will discuss the parametric equation of a circle, derive the formulas, and explore examples to understand the concept thoroughly.
Understanding Parametric Equations
In general, a parametric equation describes a curve by expressing each coordinate (x and y) as functions of an independent parameter, usually denoted as ![]() . For a circle,
. For a circle, ![]() typically represents an angle, and trigonometric functions like sine and cosine are used to express the relationship between
typically represents an angle, and trigonometric functions like sine and cosine are used to express the relationship between ![]() and
and ![]() coordinates along the circle.
coordinates along the circle.
The beauty of parametric equations lies in the fact that they allow us to control the movement along the curve by changing ![]() , making this representation particularly useful in animation and modeling circular paths.
, making this representation particularly useful in animation and modeling circular paths.
Standard Form of the Parametric Equation of a Circle
For a circle of radius ![]() centered at the origin
centered at the origin ![]() , the parametric equations are:
, the parametric equations are:
![]()
![]()
where:
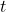 is the parameter, typically ranging from
is the parameter, typically ranging from 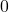 to
to 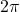 .
. is the radius of the circle.
is the radius of the circle.
This representation is derived from the basic trigonometric functions for a unit circle, where each angle ![]() corresponds to a unique point
corresponds to a unique point ![]() on the circle.
on the circle.
Why These Equations Work
The parametric equations are based on the fact that, in trigonometry, the sine and cosine of an angle represent the coordinates of a point on a unit circle (a circle with radius 1) centered at the origin. By multiplying by ![]() , we can scale this unit circle to any desired radius.
, we can scale this unit circle to any desired radius.
Example 1: Parametric Equation of a Unit Circle
For a unit circle centered at the origin (where ![]() ), the equations simplify to:
), the equations simplify to:
![]()
![]()
As ![]() varies from
varies from ![]() to
to ![]() , the point
, the point ![]() traces out a full circle of radius 1.
traces out a full circle of radius 1.
General Parametric Equation of a Circle
If the circle is not centered at the origin but instead has a center at some point ![]() , we adjust the parametric equations to account for this shift in position. The general parametric equations for a circle with radius
, we adjust the parametric equations to account for this shift in position. The general parametric equations for a circle with radius ![]() and center
and center ![]() are:
are:
![]()
![]()
where:
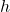 and
and 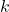 define the center of the circle.
define the center of the circle. is the radius.
is the radius.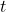 still ranges from
still ranges from 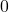 to
to 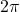 .
.
These equations allow us to draw a circle of any radius, centered at any point in the coordinate plane.
Example 2: Circle with Center at (2, -3) and Radius 5
Suppose we have a circle with center ![]() and radius
and radius ![]() . The parametric equations are:
. The parametric equations are:
![]()
![]()
As ![]() ranges from
ranges from ![]() to
to ![]() , the point
, the point ![]() will trace out a circle of radius 5 centered at
will trace out a circle of radius 5 centered at ![]() .
.
Derivation of the Parametric Equations for a Circle
The derivation of the parametric equations for a circle begins with the definition of a circle as the set of points that are equidistant from a fixed point (the center). Mathematically, for a circle with radius ![]() centered at
centered at ![]() , any point
, any point ![]() on the circle satisfies the equation:
on the circle satisfies the equation:
![]()
By parameterizing this equation, we introduce an angle ![]() and express
and express ![]() and
and ![]() in terms of trigonometric functions:
in terms of trigonometric functions:
1. Set ![]() and
and ![]() .
.
2. Then, solve for ![]() and
and ![]() to get:
to get:
![]()
![]()
These equations define the circle parametrically, allowing us to represent every point on the circle as ![]() varies.
varies.
Applications of Parametric Equations of a Circle
Parametric equations of circles are widely used in various real-world applications, especially where circular paths or oscillatory motion is involved.
1. Physics: Modeling Circular Motion
In physics, parametric equations of circles are commonly used to model circular motion. If an object moves in a circular path, the parametric equations can describe its position at any given time.
Example: Consider an object moving in a circular orbit with radius 10 units, centered at the origin. The parametric equations ![]() and
and ![]() describe its position as a function of
describe its position as a function of ![]() . By changing
. By changing ![]() over time, we can simulate the motion of the object around the circle.
over time, we can simulate the motion of the object around the circle.
2. Computer Graphics and Animation
In computer graphics, parametric equations of circles are often used to render circles and simulate rotations. They enable precise control over circular shapes, which is essential in 2D and 3D graphics.
Example: To animate a ball moving in a circular path around a central point, we can use the parametric equations with a specified radius and center. By updating the parameter ![]() incrementally, the ball will appear to move smoothly along the circular path.
incrementally, the ball will appear to move smoothly along the circular path.
3. Engineering: Describing Rotational Motion
In engineering, especially in mechanical design, circular paths are common in rotating gears, wheels, and other machinery components. Parametric equations allow engineers to describe the rotational motion of these parts.
Example: In a rotating fan, the tip of each blade follows a circular path. By representing this path using parametric equations with radius equal to the blade length, engineers can analyze the blade’s movement, speed, and position at any given time.
Plotting a Circle Using Parametric Equations
One of the main benefits of parametric equations for a circle is their ease of plotting. By plugging in values of ![]() from
from ![]() to
to ![]() , we can obtain the coordinates
, we can obtain the coordinates ![]() of points on the circle. Here’s a step-by-step example of plotting a circle parametrically:
of points on the circle. Here’s a step-by-step example of plotting a circle parametrically:
Example 3: Plotting a Circle with Radius 3 Centered at (1, 1)
Consider a circle with center ![]() and radius
and radius ![]() . The parametric equations are:
. The parametric equations are:
![]()
![]()
To plot this circle, we can:
1. Choose several values for ![]() between
between ![]() and
and ![]() .
.
2. Calculate the corresponding ![]() and
and ![]() coordinates for each
coordinates for each ![]() value.
value.
3. Plot each point ![]() on a graph and connect them to form the circle.
on a graph and connect them to form the circle.
Some sample calculations:
- For
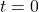 :
: 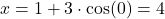 and
and 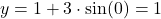 .
. - For
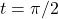 :
:  and
and 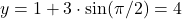 .
. - For
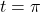 :
: 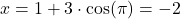 and
and 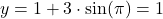 .
. - For
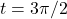 :
:  and
and 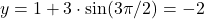 .
.
By plotting these points and connecting them, we get a complete circle of radius 3 centered at ![]() .
.
Advantages of Parametric Equations for Circles
The parametric representation of a circle offers several advantages:
1. Smooth Representation: By adjusting ![]() , parametric equations provide a continuous representation, making them suitable for animations.
, parametric equations provide a continuous representation, making them suitable for animations.
2. Control Over Position: We can easily change the center and radius of the circle by modifying ![]() ,
, ![]() , and
, and ![]() in the equations
in the equations
.
3. Flexibility: Parametric equations are useful for modeling rotational and circular motion, which appear frequently in physics and engineering applications.
Conclusion
The parametric equations of a circle, ![]() and
and ![]() , provide an efficient and flexible way to describe circles and circular motion. By representing each point on the circle as a function of an angle
, provide an efficient and flexible way to describe circles and circular motion. By representing each point on the circle as a function of an angle ![]() , we gain control over the circle’s position and size, enabling precise modeling of circles in various applications. From plotting to physics simulations and engineering, parametric equations for circles play a crucial role in helping us understand and manipulate circular paths. Whether in animations, simulations, or design, parametric equations of circles offer a powerful tool for describing circular shapes and movements.
, we gain control over the circle’s position and size, enabling precise modeling of circles in various applications. From plotting to physics simulations and engineering, parametric equations for circles play a crucial role in helping us understand and manipulate circular paths. Whether in animations, simulations, or design, parametric equations of circles offer a powerful tool for describing circular shapes and movements.