Planck’s Quantum Theory: Foundations, Principles, and Applications

Planck’s Quantum Theory, proposed by German physicist Max Planck in 1900, revolutionized our understanding of energy and light, laying the foundation for quantum mechanics. Planck introduced the concept of quantization, suggesting that energy is not continuous but instead exists in discrete packets, or “quanta.” This groundbreaking idea was initially developed to explain blackbody radiation, a phenomenon that classical physics could not adequately describe. Planck’s Quantum Theory not only resolved this paradox but also set the stage for further advancements in physics, leading to the development of modern quantum mechanics and impacting numerous fields, from atomic physics to chemistry and technology.

This article explores Planck’s Quantum Theory, its key principles, the revolutionary equation introduced by Planck, and its profound applications. Examples are provided to help illustrate these concepts.

The Background: Blackbody Radiation Problem

Before Planck’s discovery, physicists faced a major challenge known as the “blackbody radiation problem.” A blackbody is an idealized object that absorbs all electromagnetic radiation (light) incident upon it, emitting radiation in the form of heat as it approaches thermal equilibrium. According to classical physics, particularly the laws of electromagnetism and thermodynamics, a blackbody should emit radiation in a continuous spectrum across all wavelengths, with energy increasing sharply at shorter wavelengths.

This classical prediction, called the “ultraviolet catastrophe,” implied that an object would emit infinite energy at shorter wavelengths (such as ultraviolet light). Experimentally, however, it was observed that the radiation emitted by blackbodies peaked at certain wavelengths and dropped off at both higher and lower frequencies, contradicting the classical model.

Planck’s Hypothesis and Quantum Theory

In 1900, Planck proposed a radical solution to the blackbody radiation problem by introducing the concept of quantized energy levels. He suggested that energy is emitted or absorbed by matter in discrete units or “quanta” rather than in a continuous flow. Planck’s hypothesis transformed our understanding of energy by proposing that energy levels were inherently quantized.

Key Concepts of Planck’s Quantum Theory

1. Energy Quantization: Planck proposed that energy is quantized, meaning it is not emitted continuously but in fixed amounts, called “quanta.” According to this idea, the energy of a quantum is proportional to the frequency of the radiation.

2. Planck’s Equation: Planck introduced a groundbreaking equation to calculate the energy of a quantum:

$E = h \cdot \nu$

where:
– $E$ is the energy of a single quantum (photon),
– $h$ is Planck’s constant ( $6.626 \times 10^{-34} \, \text{Js}$ ),
– $\nu$ (or $f$ ) is the frequency of the radiation.

3. Planck’s Constant: Planck introduced a new constant, $h$ , now known as Planck’s constant, which quantifies the relationship between the frequency of radiation and the energy of each quantum. Planck’s constant is a fundamental constant in physics, critical to all of quantum mechanics.

Interpretation of Planck’s Theory

According to Planck’s theory, energy could only be transferred in discrete amounts rather than as a continuous wave. This quantized nature of energy transfer meant that electromagnetic radiation behaves like a series of particles (or photons), each carrying a fixed energy, rather than as a simple wave. This was a groundbreaking departure from classical physics, which treated light as a continuous wave.

Planck’s theory, therefore, introduced the “wave-particle duality” of light, which states that light can behave both as a wave and as a particle. This duality later became a foundational principle of quantum mechanics.

Example of Energy Quantization

Consider a photon of red light with a frequency of $4.3 \times 10^{14} \, \text{Hz}$ . Using Planck’s equation, we can calculate the energy of a single quantum (photon) of this light.

$E = h \cdot \nu = (6.626 \times 10^{-34}) \cdot (4.3 \times 10^{14}) = 2.85 \times 10^{-19} \, \text{J}$

Thus, each photon of red light has an energy of approximately $2.85 \times 10^{-19}$ joules.

Derivation of Planck’s Law of Blackbody Radiation

Building on his hypothesis, Planck derived an equation, known as Planck’s Law, to describe the spectral distribution of radiation emitted by a blackbody. This law gives the intensity of radiation emitted at a particular frequency (or wavelength) at a given temperature.

The formula for Planck’s Law is:

$E(\nu, T) = \frac{8 \pi h \nu^3}{c^3} \cdot \frac{1}{e^{\frac{h \nu}{k T}} - 1}$

where:

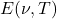$E(\nu, T)$ is the energy density at frequency 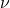$\nu$ and temperature $T$ ,
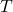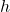$h$ is Planck’s constant,
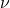$\nu$ is the frequency of radiation,
$c$ is the speed of light,
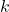$k$ is Boltzmann’s constant ( $1.38 \times 10^{-23} \, \text{J/K}$ ),
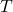$T$ is the temperature in Kelvin.

Planck’s Law accurately predicts the observed blackbody radiation spectrum across all wavelengths and resolves the ultraviolet catastrophe by indicating that radiation intensity drops off at shorter wavelengths.

Example of Planck’s Law

If we consider a blackbody at a high temperature, like the surface of the Sun (about 5,778 K), we can use Planck’s Law to predict the wavelengths of light most intensely emitted by the Sun, which peak around visible wavelengths. This explains why the Sun emits light that appears white or yellow to our eyes.

Applications of Planck’s Quantum Theory

Planck’s Quantum Theory has had a profound impact on physics, leading to numerous applications in science, technology, and even medicine. Below are some key applications:

1. Quantum Mechanics and Atomic Models

Planck’s Quantum Theory laid the foundation for the development of quantum mechanics, which describes the behavior of particles on atomic and subatomic scales. Quantum mechanics has enabled the creation of atomic models that explain electron behavior, chemical bonding, and the periodic table. Niels Bohr, for instance, used quantization to describe electron orbits in atoms, providing an explanation for atomic spectra.

Example: In the Bohr model of the hydrogen atom, electrons exist in quantized orbits with fixed energy levels. When an electron jumps from a higher energy level to a lower one, it emits a photon of energy equal to the difference between these levels, creating a spectral line.

2. Photovoltaics and Solar Cells

Solar cells, which convert sunlight into electrical energy, operate based on the principles of quantum theory. Photons from sunlight, each with quantized energy, strike the surface of a solar cell. When these photons have sufficient energy, they excite electrons in the semiconductor material, creating an electric current. This process is directly linked to Planck’s concept of quantized energy.

Example: Silicon-based solar cells use the quantized energy from sunlight to excite electrons in silicon atoms, producing a steady flow of electric current and generating power for electrical devices.

3. Spectroscopy and Atomic Emission Spectra

Planck’s Quantum Theory helps explain atomic and molecular spectra, which arise when electrons transition between quantized energy levels, emitting or absorbing photons of specific frequencies. Spectroscopy techniques, which measure these frequencies, are crucial for identifying elements, understanding chemical compositions, and studying astronomical phenomena.

Example: Spectroscopes use quantum principles to analyze the light emitted by stars. Each element has a unique spectral fingerprint due to its quantized energy levels, allowing astronomers to identify the elements present in distant stars and galaxies.

4. Quantum Computing

Quantum computing is an emerging field based on quantum mechanics, where data processing relies on qubits, which can exist in multiple states simultaneously. Quantum computers leverage superposition, entanglement, and quantized states to perform computations at unprecedented speeds, promising breakthroughs in areas like cryptography, optimization, and complex simulations.

Example: Quantum computers use qubits that take advantage of quantum superposition and entanglement, properties that are based on Planck’s quantum principles, enabling them to process large amounts of data in ways that classical computers cannot.

5. Medical Imaging and Laser Technology

Medical imaging techniques, such as MRI (Magnetic Resonance Imaging) and laser technologies, rely on quantum principles. MRI uses the magnetic properties of atomic nuclei, which exhibit quantized energy states, to create detailed images of the body’s internal structures. Lasers, which emit coherent light, operate by stimulating atoms to release photons with quantized energy, producing highly focused and intense beams.

Example: In MRI, the spin states of hydrogen nuclei in water molecules are manipulated to produce images of the body. These nuclei have quantized energy levels that allow for precise manipulation in magnetic fields, resulting in clear images for medical diagnosis.

The Impact of Planck’s Quantum Theory

Planck’s Quantum Theory had a profound impact on science, leading to the field of quantum mechanics and fundamentally altering our understanding of the universe. The theory introduced new concepts such as quantized energy levels, wave-particle duality, and the uncertainty principle, all of which are foundational to modern physics.

Key Impacts of Quantum Theory

1. Challenged Classical Physics: Quantum Theory overturned classical ideas of energy and matter

, showing that particles do not always behave deterministically but exhibit probabilistic behavior.
2. Wave-Particle Duality: Planck’s work, later extended by Einstein and de Broglie, demonstrated that particles like photons have wave-like properties, leading to the understanding that all particles exhibit both particle and wave characteristics.
3. Heisenberg’s Uncertainty Principle: Heisenberg’s principle, derived from quantum mechanics, states that the position and momentum of a particle cannot both be precisely measured simultaneously, introducing the idea of inherent uncertainty at the quantum level.

Future Prospects of Quantum Theory

Planck’s Quantum Theory has paved the way for future advancements in technology, including quantum computing, advanced materials, and nanotechnology. Research in quantum mechanics continues to expand, with applications emerging in fields as diverse as communications, energy storage, and biological systems.

Conclusion

Planck’s Quantum Theory marks one of the most significant turning points in the history of physics, offering a new way to understand energy, light, and atomic structure. By proposing that energy is quantized, Planck resolved the blackbody radiation problem and set the stage for quantum mechanics, a framework that has revolutionized our understanding of the universe. Through Planck’s Theory, scientists have developed atomic models, improved spectroscopy techniques, enabled the design of solar cells, and explored cutting-edge fields like quantum computing. Planck’s work continues to influence science and technology, making quantum mechanics a cornerstone of modern physics and one of the most transformative theories of the 20th century.