In probability and statistics, symbols and notations represent various mathematical concepts and functions, enabling us to communicate complex ideas clearly and concisely. From basic symbols like the probability function ![]() to more advanced notations like summation
to more advanced notations like summation ![]() , understanding these symbols is essential for interpreting data, conducting statistical analyses, and solving probability problems.
, understanding these symbols is essential for interpreting data, conducting statistical analyses, and solving probability problems.

This article explores key symbols in probability and statistics, explaining their meanings and providing examples to illustrate how each symbol is used in practice.
1. Probability Symbols
Probability symbols represent concepts and functions in probability theory, including the likelihood of events, random variables, and probability distributions.
1.1 Probability Function 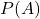
The probability function ![]() denotes the probability of event
denotes the probability of event ![]() occurring. It is a measure between 0 and 1, where 0 means the event is impossible, and 1 means the event is certain.
occurring. It is a measure between 0 and 1, where 0 means the event is impossible, and 1 means the event is certain.
Example:
Suppose we roll a fair six-sided die. The probability of rolling a 4 (event ![]() ) is represented as:
) is represented as:
![]()
So, ![]() .
.
1.2 Complement of an Event 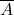 or
or 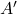
The complement of an event ![]() (or sometimes written as
(or sometimes written as ![]() ) represents the probability of event
) represents the probability of event ![]() not occurring. It is calculated as:
not occurring. It is calculated as:
![]()
Example:
If the probability of it raining tomorrow (event ![]() ) is 0.3, the probability of it not raining (complement
) is 0.3, the probability of it not raining (complement ![]() ) is:
) is:
![]()
1.3 Union of Two Events 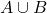
The union of two events ![]() represents the probability that either event
represents the probability that either event ![]() or event
or event ![]() (or both) occurs. If the events are mutually exclusive (cannot happen simultaneously), then:
(or both) occurs. If the events are mutually exclusive (cannot happen simultaneously), then:
![]()
For non-mutually exclusive events, we subtract the probability of both events occurring:
![]()
Example:
Suppose event ![]() is “rolling an even number” and event
is “rolling an even number” and event ![]() is “rolling a number greater than 3” on a six-sided die. We calculate:
is “rolling a number greater than 3” on a six-sided die. We calculate:
Thus:
![]()
1.4 Intersection of Two Events 
The intersection of two events ![]() represents the probability that both events
represents the probability that both events ![]() and
and ![]() occur simultaneously.
occur simultaneously.
Example:
Using the previous example of rolling a six-sided die, if ![]() is “rolling an even number” and
is “rolling an even number” and ![]() is “rolling a number greater than 3,” then the intersection
is “rolling a number greater than 3,” then the intersection ![]() includes the outcomes {4, 6}. Therefore:
includes the outcomes {4, 6}. Therefore:
![]()
2. Random Variables and Distribution Symbols
Random variables and distribution symbols are central in probability theory, as they represent quantities that result from random events.
2.1 Random Variable 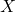
A random variable ![]() is a variable representing outcomes of a random phenomenon, which can take on various values depending on the result of the experiment. Random variables are often classified as either discrete (countable outcomes) or continuous (uncountable outcomes).
is a variable representing outcomes of a random phenomenon, which can take on various values depending on the result of the experiment. Random variables are often classified as either discrete (countable outcomes) or continuous (uncountable outcomes).
Example:
Consider a random variable ![]() that represents the outcome of a six-sided die roll. The values of
that represents the outcome of a six-sided die roll. The values of ![]() are \{1, 2, 3, 4, 5, 6\}, each representing a possible outcome of the die roll.
are \{1, 2, 3, 4, 5, 6\}, each representing a possible outcome of the die roll.
2.2 Expected Value 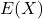
The expected value ![]() of a random variable
of a random variable ![]() represents the mean or average outcome of the random variable over numerous trials. For a discrete random variable,
represents the mean or average outcome of the random variable over numerous trials. For a discrete random variable, ![]() is calculated as:
is calculated as:
![]()
where ![]() are the possible values of
are the possible values of ![]() and
and ![]() is the probability of each value.
is the probability of each value.
Example:
If a fair die is rolled, the expected value ![]() of a random variable
of a random variable ![]() representing the outcome is:
representing the outcome is:
![]()
2.3 Variance 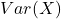
Variance ![]() measures the spread or variability of a random variable
measures the spread or variability of a random variable ![]() around its mean. Variance is calculated as:
around its mean. Variance is calculated as:
![]()
Example:
For a fair six-sided die roll, with ![]() , we calculate:
, we calculate:
![Rendered by QuickLaTeX.com \[ Var(X) = \sum_{i=1}^{6} \left( x_i - 3.5 \right)^2 \times \frac{1}{6} \]](https://www.sridianti.com/wp-content/uploads/2024/10/quicklatex.com-5ce09b8703e12247a39df7fef9ebd916_l3.png)
The result gives us the average squared deviation of each outcome from the expected value.
3. Distribution Symbols
3.1 Probability Density Function (PDF) 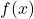
The probability density function (PDF) ![]() describes the likelihood of different outcomes for a continuous random variable. For continuous distributions, the area under the PDF curve between two values represents the probability that the random variable falls within that range.
describes the likelihood of different outcomes for a continuous random variable. For continuous distributions, the area under the PDF curve between two values represents the probability that the random variable falls within that range.
Example:
The normal distribution has a bell-shaped PDF:
![]()
where ![]() is the mean and
is the mean and ![]() is the standard deviation.
is the standard deviation.
3.2 Cumulative Distribution Function (CDF) 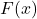
The cumulative distribution function (CDF) ![]() represents the probability that a random variable
represents the probability that a random variable ![]() takes on a value less than or equal to
takes on a value less than or equal to ![]() :
:
![]()
Example:
For a random variable with a standard normal distribution, ![]() represents the probability that
represents the probability that ![]() is less than or equal to 0, which is approximately 0.5, as the standard normal distribution is symmetric about the mean.
is less than or equal to 0, which is approximately 0.5, as the standard normal distribution is symmetric about the mean.
4. Common Statistical Symbols
4.1 Mean 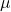 and Sample Mean
and Sample Mean 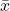
- Population Mean (
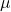 ) is the average of all data points in a population.
) is the average of all data points in a population. - Sample Mean (
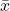 ) is the average of a sample subset from a larger population.
) is the average of a sample subset from a larger population.
![]()
Example:
If we have a sample dataset of exam scores \{85, 90, 75, 95\}, the sample mean is:
![]()
4.2 Standard Deviation 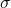 and Sample Standard Deviation
and Sample Standard Deviation 
- Population Standard Deviation (
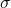 ) represents the average distance of each data point from the mean for an entire population.
) represents the average distance of each data point from the mean for an entire population. - Sample Standard Deviation (
 ) represents this average distance within a sample subset.
) represents this average distance within a sample subset.
![Rendered by QuickLaTeX.com \[ s = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n - 1}} \]](https://www.sridianti.com/wp-content/uploads/2024/10/quicklatex.com-e9f0d700c8356dfac6c8b0a22875ffb0_l3.png)
Example:
Using the sample dataset \{85, 90, 75, 95\}, we calculate the sample standard deviation ![]() , which gives us a measure of how spread out the scores are around the sample mean.
, which gives us a measure of how spread out the scores are around the sample mean.
4.3 Variance 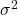 and Sample Variance
and Sample Variance 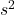
- Population Variance (
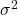 ) is the square of the population standard deviation.
) is the square of the population standard deviation. - Sample Variance (
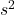 ) is the square of the sample
) is the square of the sample
standard deviation.
![]()
5. Summation 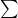 and Product
and Product 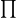
- Summation (
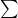 ) denotes the addition of a series of terms.
) denotes the addition of a series of terms.
![]()
- Product (
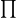 ) denotes the multiplication of a series of terms.
) denotes the multiplication of a series of terms.
![]()
Example:
For the set \{2, 3, 4\},
- Summation:
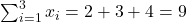
- Product:
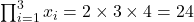
Conclusion
Understanding probability and statistics symbols is essential for analyzing data, solving probability problems, and interpreting results. Symbols like ![]() ,
, ![]() ,
, ![]() , and
, and ![]() allow us to communicate complex concepts effectively, aiding in calculations and data interpretation. With this guide, these fundamental symbols become clearer, enabling better comprehension and application in various statistical and probability contexts.
allow us to communicate complex concepts effectively, aiding in calculations and data interpretation. With this guide, these fundamental symbols become clearer, enabling better comprehension and application in various statistical and probability contexts.