Projectile Motion: Concepts, Equations, and Applications

Projectile motion is a type of two-dimensional motion in which an object is projected into the air and moves under the influence of gravity. This motion is characterized by a parabolic trajectory, determined by the object’s initial velocity, the angle of projection, and the acceleration due to gravity. Understanding projectile motion is fundamental in physics, engineering, and sports science, as it helps predict and analyze the behavior of objects in free flight.

This article explores the principles of projectile motion, derives its governing equations, and provides examples to illustrate its applications in real-life scenarios.

Understanding Projectile Motion

Projectile motion occurs when an object is launched into the air and moves under the combined influence of an initial velocity and the downward acceleration due to gravity. It assumes the absence of air resistance, simplifying the motion into two components:
1. Horizontal Motion: Constant velocity, as no horizontal acceleration acts on the object.
2. Vertical Motion: Accelerated motion under the influence of gravity, causing the object to decelerate as it rises and accelerate as it falls.

Key Characteristics of Projectile Motion

1. Trajectory: The path followed by a projectile is parabolic, due to the interplay of horizontal and vertical motions.
2. Independence of Components: The horizontal and vertical motions are independent of each other and are analyzed separately.
3. Gravity’s Role: Gravity acts only in the vertical direction, affecting the object’s vertical velocity while leaving its horizontal velocity unchanged.

Example: When a soccer ball is kicked at an angle, it follows a parabolic trajectory. The horizontal motion is uniform, while the vertical motion is influenced by gravity.

Equations of Projectile Motion

The equations of projectile motion are derived from kinematic equations, which describe the motion of objects under constant acceleration. For simplicity, we assume the object is launched from ground level.

1. Horizontal Motion

The horizontal displacement ( $x$ ) of a projectile is determined by its constant horizontal velocity ( $v_x$ ) and time ( $t$ ):

$x = v_x \cdot t$

Since the horizontal velocity remains constant, $v_x$ is:

$v_x = v \cdot \cos \theta$

where:

$v$ is the initial velocity,
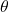$\theta$ is the angle of projection.

2. Vertical Motion

The vertical displacement ( $y$ ) of a projectile is influenced by gravity, leading to accelerated motion:

$y = v_y \cdot t - \frac{1}{2} g t^2$

Here, the initial vertical velocity ( $v_y$ ) is:

$v_y = v \cdot \sin \theta$

where:

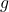$g$ is the acceleration due to gravity ( $9.8 \, \text{m/s}^2$ ).

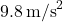The vertical velocity ( $v_y$ ) at any time $t$ is given by:

$v_y = v \cdot \sin \theta - g \cdot t$

3. Time of Flight

The total time ( $T$ ) a projectile remains in the air depends on its initial vertical velocity and gravity. The time of flight is derived from the vertical motion equation when the object returns to its initial height ( $y = 0$ ):

$T = \frac{2 v \cdot \sin \theta}{g}$

4. Maximum Height

The maximum height ( $H$ ) is the highest vertical position reached by the projectile. It occurs when the vertical velocity becomes zero ( $v_y = 0$ ):

$H = \frac{(v \cdot \sin \theta)^2}{2g}$

5. Range

The horizontal range ( $R$ ) is the total horizontal distance traveled by the projectile before hitting the ground. It depends on the horizontal velocity and time of flight:

$R = v_x \cdot T$

Substituting $T$ into the range equation:

$R = \frac{v^2 \cdot \sin 2\theta}{g}$

where $\sin 2\theta = 2 \cdot \sin \theta \cdot \cos \theta$ .

Combined Equation for Trajectory

The trajectory of a projectile, $y$ as a function of $x$ , is given by eliminating $t$ from the horizontal and vertical equations:

$y = x \cdot \tan \theta - \frac{g \cdot x^2}{2 \cdot (v \cdot \cos \theta)^2}$

This equation describes the parabolic path of the projectile.

Example Problems and Solutions

Example 1: Calculating the Range and Time of Flight

Problem: A ball is thrown with an initial velocity of $20 \, \text{m/s}$ at an angle of $30^\circ$ . Find the time of flight and horizontal range.

Solution:

1. Time of Flight:

$T = \frac{2 \cdot v \cdot \sin \theta}{g}$

Substituting values:

$T = \frac{2 \cdot 20 \cdot \sin 30^\circ}{9.8} = \frac{20 \cdot 0.5}{9.8} = 1.02 \, \text{s}$

2. Range:

$R = \frac{v^2 \cdot \sin 2\theta}{g}$

Substituting values:

$R = \frac{20^2 \cdot \sin 60^\circ}{9.8} = \frac{400 \cdot 0.866}{9.8} \approx 35.3 \, \text{m}$

Thus, the ball stays in the air for $1.02 \, \text{s}$ and travels a horizontal distance of $35.3 \, \text{m}$ .

Example 2: Determining Maximum Height

Problem: A projectile is launched with a velocity of $25 \, \text{m/s}$ at an angle of $45^\circ$ . Calculate the maximum height reached by the projectile.

Solution:

1. Maximum Height:

$H = \frac{(v \cdot \sin \theta)^2}{2g}$

Substituting values:

$H = \frac{(25 \cdot \sin 45^\circ)^2}{2 \cdot 9.8} = \frac{(25 \cdot 0.707)^2}{19.6}$

$H = \frac{12.5^2}{19.6} = \frac{156.25}{19.6} \approx 7.97 \, \text{m}$

The maximum height is $7.97 \, \text{m}$ .

Applications of Projectile Motion

Projectile motion has applications across science, engineering, and everyday life. Its principles are used to design sports equipment, plan military operations, and analyze motion in nature.

1. Sports Science

In sports like basketball, soccer, and baseball, understanding projectile motion helps athletes optimize their techniques for accuracy and performance. The angle and velocity of throws or kicks determine the trajectory of the ball.

Example: In basketball, players adjust the angle of their shots to ensure the ball follows a parabolic path and lands in the hoop.

2. Ballistics and Defense

Projectile motion is central to ballistics, where it is used to calculate the trajectory of projectiles like bullets, missiles, or artillery shells. These calculations ensure that targets are hit accurately over various ranges.

Example: The trajectory of a cannonball in historical warfare was calculated using principles of projectile motion to maximize range and accuracy.

3. Space Exploration

In space exploration, the principles of projectile motion are applied to calculate the trajectories of rockets and spacecraft, ensuring they follow the correct path to their destinations.

Example: Engineers use projectile motion equations to design the trajectory of rockets during launch, ensuring they achieve the desired orbit.

4. Civil Engineering

In construction and engineering, understanding projectile motion is essential for designing structures like bridges and calculating the motion of debris during demolition.

Example: Engineers analyze the motion of debris to ensure that controlled demolitions are safe and the debris falls within designated areas.

Factors Affecting Projectile Motion

1. Initial Velocity

Higher initial velocity increases the range, height, and time of flight of a projectile.

2. Angle of Projection

The optimal angle for maximum range is $45^\circ$ . Angles less than $45^\circ$ result in shorter ranges due to reduced vertical motion, while angles greater than $45^\circ$ reduce range due to lower horizontal motion.

3. Gravity

Gravity acts downward, reducing the vertical component of velocity and pulling the projectile back to the ground. Variations in gravitational acceleration (e.g., on the Moon or Mars) affect projectile trajectories.

4. Air Resistance (Neglected Here)

In real-world scenarios, air resistance can significantly alter the trajectory, reducing range and height.

Conclusion

Projectile motion is a fundamental concept in physics, combining horizontal and vertical motions to create a parabolic trajectory. By understanding the equations governing this motion, scientists and engineers can predict and optimize the behavior of projectiles in sports, military applications, space exploration, and engineering. Whether calculating

the range of a cannonball or the arc of a soccer ball, the principles of projectile motion offer a powerful framework for analyzing two-dimensional motion.