A triangle is a fundamental shape in geometry, characterized by its three sides, three angles, and three vertices. It is one of the simplest yet most versatile polygons, serving as a building block for many complex shapes and structures. Triangles are not only crucial in mathematics but also appear frequently in engineering, architecture, art, and nature. Understanding the properties of triangles allows us to solve problems related to area, perimeter, angles, and symmetry.

In this article, we will delve into the different properties of triangles, including types of triangles, properties of angles, side properties, and special points such as centroids and orthocenters. We will also explore how these properties interact with each other and provide practical examples to illustrate each concept.
What Is a Triangle?
A triangle is a polygon with three sides (line segments), three vertices (corner points), and three angles formed where the sides meet. It is the simplest polygon and can be classified based on side length and angle measures. The most basic property of a triangle is that the sum of the internal angles is always 180 degrees.
- Sum of Angles in a Triangle: One of the fundamental properties of a triangle is that the sum of its internal angles is always 180°. This rule holds true for all types of triangles, regardless of their size or shape.
- Example: Consider a triangle with angles of 60°, 70°, and 50°. Adding these angles gives us 60° + 70° + 50° = 180°, confirming that the triangle’s angles adhere to this rule.
- Types of Triangles Based on Angles: Triangles can be classified into three types based on their angles:
- Acute Triangle: All angles are less than 90°.
- Right Triangle: One angle is exactly 90°.
- Obtuse Triangle: One angle is greater than 90°.
- Example: A right triangle with angles 90°, 45°, and 45° is used in trigonometry and construction, such as when creating ramps or roofs.
- Types of Triangles Based on Sides: Triangles are also categorized based on the length of their sides:
- Equilateral Triangle: All three sides are equal in length, and all angles are 60°.
- Isosceles Triangle: Two sides are equal, and the angles opposite those sides are equal.
- Scalene Triangle: All sides and angles are different.
- Example: An equilateral triangle is often used in art and design for its symmetry, while an isosceles triangle is common in bridge structures where equal support is required.
Properties of Angles in a Triangle
The angles within a triangle reveal much about its shape and can be used to solve for unknown measurements using trigonometric relationships and geometric theorems.
- Exterior Angles: An exterior angle of a triangle is formed when one side of the triangle is extended outward. The exterior angle is always equal to the sum of the two opposite interior angles. This property is often used in geometric proofs and calculations.
- Example: In a triangle with interior angles 40° and 60°, the exterior angle at the third vertex would be 100° because 40° + 60° = 100°.
- Angle Bisectors: An angle bisector is a line or ray that divides an angle of the triangle into two equal angles. Each triangle has three angle bisectors, and they intersect at a point called the incenter, which is the center of the inscribed circle (incircle) of the triangle.
- Example: In an isosceles triangle with angles 80°, 50°, and 50°, the angle bisector of the 50° angle will divide it into two 25° angles, making it easier to find the incenter and determine properties of the incircle.
- Triangle Inequality Theorem: This theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side. This property ensures that three given lengths can form a valid triangle.
- Example: If a triangle has side lengths of 3 cm, 4 cm, and 5 cm, it satisfies the triangle inequality because:
- 3 + 4 > 5
- 3 + 5 > 4
- 4 + 5 > 3
- Example: If a triangle has side lengths of 3 cm, 4 cm, and 5 cm, it satisfies the triangle inequality because:
Properties of Sides in a Triangle
The sides of a triangle determine its shape, size, and symmetry. The relationships between the sides, angles, and area are crucial for solving problems in geometry and trigonometry.
- Pythagorean Theorem: This is a key property of right triangles. It states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
- Formula: a2+b2=c2, where cc is the hypotenuse, and aa and bb are the other two sides.
- Example: In a right triangle with sides 3 cm and 4 cm, the hypotenuse can be found using the formula: 32+42=9+16=25, so c=√25 cm.
- Law of Sines: The Law of Sines relates the ratios of the lengths of sides of a triangle to the sines of their opposite angles. This law is useful in solving for unknown sides or angles in non-right triangles.
- Formula:
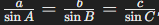 , where aa, bb, and cc are the sides opposite angles A, B, and C.
, where aa, bb, and cc are the sides opposite angles A, B, and C. - Example: In a triangle with sides 8 cm and 10 cm opposite angles 30° and 45° respectively, the Law of Sines can help determine the third side or angle by solving the equation.
- Formula:
- Perimeter and Area: The perimeter of a triangle is the sum of the lengths of its sides, while the area is the space enclosed by the triangle. The area can be calculated using various formulas, depending on the information available.
- Formula for Area: Area=1/2×base×height .
- Example: For a triangle with a base of 6 cm and a height of 4 cm, the area is 1/2×6×4=12 square cm.
- Heron’s Formula: Used when the lengths of all three sides are known:
-
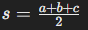
- Area=√s(s−a)(s−b)(s−c), where ss is the semi-perimeter.
-
- Example: A triangle with sides 7 cm, 8 cm, and 9 cm has a semi-perimeter of 12 cm. Using Heron’s formula, the area can be calculated as:
- Area=√(12(12−7)(12−8)(12−9)=√(12×5×4×3)=√720=26.83 cm2.
Special Points in a Triangle
Every triangle has several special points—centroid, orthocenter, circumcenter, and incenter—each with unique properties and significance in geometric constructions.
- Centroid: The centroid is the point where the three medians (lines drawn from a vertex to the midpoint of the opposite side) intersect. It acts as the center of gravity of the triangle and divides each median into a ratio of 2:1.
- Example: In a triangle with vertices at (0, 0), (4, 0), and (2, 6), the centroid can be found by averaging the coordinates:
- Centroid=
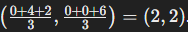 .
.
- Centroid=
- Example: In a triangle with vertices at (0, 0), (4, 0), and (2, 6), the centroid can be found by averaging the coordinates:
- Orthocenter: The orthocenter is the point where the altitudes (perpendicular lines from a vertex to the opposite side) of a triangle intersect. The location of the orthocenter depends on the type of triangle:
- Inside the triangle for acute triangles.
- At the vertex of the right angle for right triangles.
- Outside the triangle for obtuse triangles.
- Example: In a right triangle with vertices (0, 0), (3, 0), and (0, 4), the orthocenter is at the vertex (0, 0) because it is the right-angle vertex.
- Circumcenter: The circumcenter is the point where the perpendicular bisectors of the sides of a triangle intersect. It is the center of the circumcircle (the circle that passes through all three vertices of the triangle).
- Example: In an equilateral triangle, the circumcenter lies at the same point as the centroid and incenter, equidistant from all three vertices, which makes it easier to draw the circumcircle.
- Incenter: The incenter is the point where the angle bisectors of a triangle intersect and is the center of the incircle (the circle that touches all three sides of the triangle internally).
- Example: In a triangle with sides 7 cm, 8 cm, and 9 cm, the incenter can be found using the angle bisectors, and it determines the radius of the incircle that can be drawn inside the triangle.
Importance of Understanding Triangle Properties
Understanding the properties of triangles is essential not only in geometry but also in practical applications such as engineering, architecture, navigation, and computer graphics. Triangles are often used to divide complex shapes into simpler components, making calculations and structural designs more manageable.
- Engineering and Architecture: Triangles are integral in designing trusses, bridges, and roofs due to their structural stability. The use of right triangles in measuring heights and distances is a fundamental technique in surveying.
- Example: Triangular trusses in bridges use the rigidity of triangles to evenly distribute weight and provide stability, preventing buckling under heavy loads.
- Computer Graphics and Animation: Triangles are used in 3D modeling and animation because they can form the basis of complex surfaces. Polygonal meshes made of triangles are used to create realistic 3D shapes in video games and virtual reality.
- Example: In 3D software, a complex object like a car or character is made up of thousands of small triangles, each contributing to the overall shape and appearance.
- Astronomy and Navigation: The properties of triangles are used in trigonometry for calculating distances between stars and planets. Triangulation is a method used in GPS technology to determine positions on Earth by measuring angles from satellites.
- Example: By measuring the angles between three known points on Earth, GPS receivers can calculate the exact location of a user, providing accurate navigation for everything from smartphones to aircraft.
Conclusion
Triangles are among the most fundamental shapes in geometry, with properties that reveal much about their structure and function. From the simple rule that their angles add up to 180 degrees to the complex relationships between their sides and special points, triangles offer endless opportunities for exploration and application. Whether used in mathematical proofs, engineering projects, or computer graphics, understanding the properties of triangles is essential for solving a wide range of problems and designing efficient solutions in both theoretical and practical fields. Their versatility and importance make triangles a cornerstone of geometry and a key element in our understanding of the world.