The Hexadecimal Number System: Concepts, Conversions, and Applications

The hexadecimal number system, also known as the base-16 system, is a positional numeral system that uses sixteen symbols to represent values. In contrast to the decimal system (base-10) that uses ten digits (0–9), the hexadecimal system includes six additional symbols, represented by the letters A through F, which correspond to the decimal values 10 through 15. The hexadecimal system is widely used in computing, digital electronics, and programming, where it provides an efficient way to represent large binary values compactly.

In this article, we’ll explore the fundamental concepts behind the hexadecimal number system, understand how to convert between hexadecimal and other number systems, and examine its applications with examples to illustrate each concept.

Understanding the Hexadecimal Number System

The hexadecimal system is a base-16 number system. It includes the following symbols:

Digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, representing values 0 through 9.
Letters: A, B, C, D, E, and F, representing values 10 through 15.

Each digit in a hexadecimal number represents a power of 16, depending on its position (similar to how each digit in a decimal number represents a power of 10). The rightmost position is the “least significant” digit (16^0), and as we move left, each position increases in powers of 16.

For example, in the hexadecimal number $3A5$ , the value of each digit is calculated as:

$3 \times 16^2 + A \times 16^1 + 5 \times 16^0$

where:

$3 \times 16^2 = 768$
$A \times 16^1 = 10 \times 16 = 160$
$5 \times 16^0 = 5$

Thus, $3A5$ in hexadecimal is equal to $768 + 160 + 5 = 933$ in decimal.

Why Hexadecimal?

The hexadecimal system is particularly useful in computing and digital electronics because it provides a more compact way to represent binary numbers. Since each hexadecimal digit corresponds to exactly four binary digits (bits), it simplifies the process of reading and writing large binary values. For example, the 8-bit binary number $11011110$ can be represented more compactly as $DE$ in hexadecimal.

Hexadecimal to Decimal Conversion

To convert a hexadecimal number to decimal, expand each hexadecimal digit as a power of 16 and sum the results. Let’s go through an example.

Example: Convert 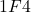$1F4$ from Hexadecimal to Decimal

1. Break down the hexadecimal number into its positional values:
– $1$ in the hundreds place (16^2),
– $F$ in the tens place (16^1),
– $4$ in the units place (16^0).

2. Substitute the values and calculate:

$1 \times 16^2 + F \times 16^1 + 4 \times 16^0$

3. Substitute $F = 15$ :

$= 1 \times 256 + 15 \times 16 + 4 \times 1$

4. Perform the calculations:

$= 256 + 240 + 4 = 500$

Thus, $1F4$ in hexadecimal is equal to $500$ in decimal.

Decimal to Hexadecimal Conversion

To convert a decimal number to hexadecimal, repeatedly divide the decimal number by 16, keeping track of the remainders. The hexadecimal representation is the sequence of remainders read from bottom to top.

Example: Convert 745 from Decimal to Hexadecimal

1. Divide 745 by 16. The quotient is 46, and the remainder is 9.
2. Divide 46 by 16. The quotient is 2, and the remainder is 14 (represented by E in hexadecimal).
3. Divide 2 by 16. The quotient is 0, and the remainder is 2.

Reading the remainders from bottom to top, 745 in decimal is represented as $2E9$ in hexadecimal.

Binary to Hexadecimal Conversion

The binary and hexadecimal systems are closely related, as four binary digits (bits) correspond to one hexadecimal digit. This relationship simplifies the conversion process between binary and hexadecimal.

Example: Convert $10111011$ from Binary to Hexadecimal

1. Break the binary number into groups of four, starting from the right: $1011$ and $1011$ .
2. Convert each group of four bits to its hexadecimal equivalent:
– $1011$ in binary is $B$ in hexadecimal.
– $1011$ in binary (again) is $B$ in hexadecimal.

Thus, $10111011$ in binary is equal to $BB$ in hexadecimal.

Hexadecimal in Computing and Digital Electronics

In computing and digital electronics, hexadecimal is commonly used because it aligns well with binary data. Digital systems, such as computers, use binary as their primary language. However, binary strings can become lengthy and challenging to interpret, which is why hexadecimal is often used as a shorthand notation.

1. Memory Addresses

In computer programming and system design, memory addresses are often represented in hexadecimal. Memory addresses are usually long binary numbers, and hexadecimal notation makes them easier to read and understand.

Example: In a computer’s memory, an address might be represented as $0x1F3B$ rather than a lengthy binary equivalent like $0001111100111011$ .

2. Color Representation in Web Design

Hexadecimal numbers are widely used in web design to represent colors. In HTML and CSS, colors are often specified as six-digit hexadecimal codes, where each pair of digits represents the red, green, and blue (RGB) values of the color.

Example: The color code $#FF5733$ represents a specific shade, with $FF$ for red, $57$ for green, and $33$ for blue. In decimal, this corresponds to 255 for red, 87 for green, and 51 for blue.

3. Machine Code and Assembly Language

Machine code, the fundamental language of computers, and assembly language often use hexadecimal notation to represent instructions and data. Hexadecimal is compact, making it easier to read and debug low-level code.

Example: In assembly language, an instruction might look like $MOV AX, 1F4H$ , where $1F4H$ is the hexadecimal representation of the decimal value 500.

4. Error Codes in Diagnostics

Hexadecimal is also used to display error codes in diagnostic software and hardware. Many computer systems use hexadecimal error codes to indicate specific issues, as hexadecimal notation provides a short and standardized format.

Example: In the Windows operating system, error codes are often displayed in hexadecimal, such as $0xC0000142$ , where each hexadecimal digit represents a specific error characteristic.

Practical Examples of Using Hexadecimal

Example 1: Network Configuration

In networking, IP addresses in IPv6 are represented in hexadecimal. IPv6 addresses consist of 128 bits, which are divided into eight groups of four hexadecimal digits.

Example: An IPv6 address like $2001:0db8:85a3:0000:0000:8a2e:0370:7334$ uses hexadecimal notation to represent each segment. This compact form replaces a much longer binary string.

Example 2: Hexadecimal in Microcontrollers

Microcontrollers and embedded systems, such as those used in consumer electronics, often rely on hexadecimal notation for programming and configuration. Programmers use hexadecimal to represent memory addresses, register values, and configuration settings.

Example: In a microcontroller, a hexadecimal address like $0x2A$ might specify a register location where data should be stored, allowing efficient management of the device’s memory and operations.

Example 3: Data Compression and File Storage

File formats and data compression systems frequently use hexadecimal to represent binary data. Many file headers and data segments use hexadecimal for easy identification and manipulation.

Example: JPEG image files include a header represented in hexadecimal to indicate the file type and metadata. For instance, a JPEG file begins with the hexadecimal sequence $FF D8 FF$ , which signals the start of a JPEG file to software applications.

Advantages of the Hexadecimal System

The hexadecimal system offers several practical advantages, especially in fields that require binary representation and manipulation:

1. Compactness: Each hexadecimal digit represents four binary digits, making it a compact way to write long binary numbers.
2. Readability: Hexadecimal numbers are easier to read and interpret than long binary strings.
3. Compatibility with Binary: Since digital electronics and computing rely on binary, hexadecimal offers an efficient way to represent binary numbers without conversion errors.
4. Ease of Debugging: In programming and hardware design, hexadecimal notation simplifies debugging and troubleshooting by offering a clear view of binary data.

Conclusion

The hexadecimal number system is a vital tool in computing, digital electronics, and data management. Its base-16 structure provides a compact and readable way to represent binary numbers, making it essential for applications like memory addressing, color representation, machine code, and diagnostics. Understanding hexadecimal allows programmers, engineers, and web designers to work more efficiently with data, streamline digital processes,

and improve system reliability. Through examples and applications, it’s clear that hexadecimal plays a critical role in modern technology and digital systems. As computing continues to evolve, the hexadecimal system will remain an indispensable asset for managing and representing complex binary information.