The Law of Conservation of Momentum: Derivation and Applications

The law of conservation of momentum is a fundamental principle of classical mechanics that governs the behavior of objects in motion. It states that the total momentum of a closed system remains constant if no external forces act on it. This principle applies universally, from everyday interactions to astrophysical phenomena, and forms the foundation of collision analysis, rocket propulsion, and fluid dynamics.

Momentum, a vector quantity defined as the product of an object’s mass and velocity, reflects the motion of an object. Understanding its conservation requires delving into Newton’s laws of motion and exploring how forces and interactions influence systems of particles. This article derives the law of conservation of momentum and illustrates its utility through practical examples.

Momentum and Newton’s Laws of Motion

Before deriving the conservation law, let us recall the definition of momentum and the laws of motion:

1. Momentum ( $\mathbf{p}$ ): Momentum is the product of an object’s mass ( $m$ ) and velocity ( $\mathbf{v}$ ):

$\mathbf{p} = m \mathbf{v}$

It is a vector quantity, meaning it has both magnitude and direction.

2. Newton’s Second Law: The rate of change of momentum of an object is equal to the net force acting on it:

$\mathbf{F} = \frac{d\mathbf{p}}{dt}$

For an object of constant mass, this becomes:

$\mathbf{F} = m \frac{d\mathbf{v}}{dt} = m \mathbf{a}$

3. Newton’s Third Law: For every action, there is an equal and opposite reaction. If object A exerts a force $\mathbf{F}_{\text{AB}}$ on object B, object B exerts an equal and opposite force $\mathbf{F}_{\text{BA}}$ on object A:

$\mathbf{F}_{\text{AB}} = -\mathbf{F}_{\text{BA}}$

Newton’s third law plays a crucial role in the conservation of momentum, as the forces between interacting bodies are equal in magnitude but opposite in direction.

Derivation of the Law of Conservation of Momentum

Consider a system of two interacting particles, A and B, in an isolated system where no external forces act.

Step 1: Write Newton’s Second Law for Each Particle

The force on particle A due to particle B is $\mathbf{F}_{\text{AB}}$ , and the force on particle B due to particle A is $\mathbf{F}_{\text{BA}}$ . From Newton’s second law:

$\mathbf{F}_{\text{AB}} = \frac{d\mathbf{p}_{\text{A}}}{dt}, \quad \mathbf{F}_{\text{BA}} = \frac{d\mathbf{p}_{\text{B}}}{dt}$

Step 2: Apply Newton’s Third Law

Newton’s third law states that $\mathbf{F}_{\text{AB}} = -\mathbf{F}_{\text{BA}}$ . Substituting this into the equations for forces:

$\frac{d\mathbf{p}_{\text{A}}}{dt} = -\frac{d\mathbf{p}_{\text{B}}}{dt}$

Step 3: Combine the Equations

Adding both equations eliminates the forces:

$\frac{d\mathbf{p}_{\text{A}}}{dt} + \frac{d\mathbf{p}_{\text{B}}}{dt} = 0$

This implies that the rate of change of the total momentum $\mathbf{p}_{\text{total}}$ is zero:

$\frac{d}{dt}(\mathbf{p}_{\text{A}} + \mathbf{p}_{\text{B}}) = 0$

Step 4: Conclude Momentum Conservation

If the time derivative of total momentum is zero, the total momentum remains constant:

$\mathbf{p}_{\text{A}} + \mathbf{p}_{\text{B}} = \text{constant}$

This result generalizes to systems with any number of particles, showing that the total momentum of an isolated system is conserved in the absence of external forces.

Examples of the Conservation of Momentum

Example 1: Collision Between Two Objects

Consider two objects, A and B, with masses $m_{\text{A}}$ and $m_{\text{B}}$ , moving in a straight line. Before the collision, their velocities are $v_{\text{A}}$ and $v_{\text{B}}$ , respectively. After the collision, their velocities change to $v_{\text{A}}'$ and $v_{\text{B}}'$ .

Applying Momentum Conservation

The total momentum before and after the collision is conserved:

$m_{\text{A}} v_{\text{A}} + m_{\text{B}} v_{\text{B}} = m_{\text{A}} v_{\text{A}}' + m_{\text{B}} v_{\text{B}}'$

Example Calculation

Suppose:

$m_{\text{A}} = 2 \, \text{kg}$ , $v_{\text{A}} = 4 \, \text{m/s}$
$m_{\text{B}} = 3 \, \text{kg}$ , $v_{\text{B}} = -2 \, \text{m/s}$
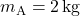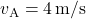
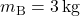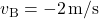
After the collision, $v_{\text{A}}' = 1 \, \text{m/s}$

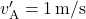
Find $v_{\text{B}}'$ :

$(2)(4) + (3)(-2) = (2)(1) + (3)v_{\text{B}}'$

$8 - 6 = 2 + 3v_{\text{B}}'$

$2 = 2 + 3v_{\text{B}}'$

$v_{\text{B}}' = 0 \, \text{m/s}$

Example 2: Rocket Propulsion

A rocket operates by ejecting exhaust gases at high speed, using the principle of momentum conservation. The system (rocket + exhaust) starts with zero momentum. As the exhaust is expelled backward, the rocket gains forward momentum to conserve the total momentum.

Applying Momentum Conservation

Let:

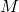$M$ : Rocket’s mass.
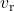$v_{\text{r}}$ : Rocket’s velocity.
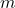$m$ : Mass of ejected gas.
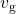$v_{\text{g}}$ : Velocity of ejected gas (relative to the rocket).

Initially, the total momentum is zero. After ejection:

$M v_{\text{r}} + m (-v_{\text{g}}) = 0$

Solving for the rocket’s velocity:

$v_{\text{r}} = \frac{m v_{\text{g}}}{M}$

This explains how rockets achieve propulsion in space, where there is no external force.

Applications of Momentum Conservation

1. Collisions in Sports: When a basketball player catches a moving ball, the player and the ball form a system whose momentum is conserved. The player’s motion adjusts to accommodate the ball’s momentum.

2. Traffic Accident Reconstruction: Conservation of momentum helps investigators determine the pre-collision speeds of vehicles involved in accidents.

3. Astrophysics: The orbital dynamics of celestial bodies, such as planets and comets, rely on momentum conservation to predict motion and interactions.

4. Explosions: During an explosion, the fragments of the object move in such a way that the total momentum of the system remains constant.

Limitations of Momentum Conservation

1. External Forces: Momentum conservation applies only in isolated systems where no external forces act. In the presence of forces like friction or gravity, external factors influence the total momentum.

2. Relativistic Effects: At speeds close to the speed of light, classical momentum conservation must be modified to account for relativistic momentum, $\mathbf{p} = \gamma m \mathbf{v}$ , where $\gamma$ is the Lorentz factor.

Conclusion

The law of conservation of momentum is a cornerstone of classical mechanics, governing the behavior of objects in motion and interactions. Derived from Newton’s laws, it provides a powerful tool for analyzing collisions, rocket propulsion, and other dynamic systems. By recognizing that the total momentum of a closed system remains constant in the absence of external forces, we gain a deeper understanding of the fundamental principles that govern our universe. Through examples and applications, the versatility and importance of momentum conservation are evident, bridging theoretical physics and practical problem-solving.