The Law of Equipartition of Energy: Theory, Formula, and Applications

The Law of Equipartition of Energy is a fundamental concept in thermodynamics and statistical mechanics. It provides a framework for understanding how energy is distributed among the various degrees of freedom (modes of motion) in a system of particles at thermal equilibrium. According to this law, energy is shared equally across all degrees of freedom that contribute to the system’s total energy. The law is particularly useful in describing the behavior of gases, as it allows scientists and engineers to predict the distribution of kinetic and potential energy among particles based on temperature.

This article will explore the theoretical foundation of the Law of Equipartition of Energy, its mathematical formulation, and applications in various physical systems, with examples that demonstrate how energy distribution operates at the microscopic level.

What Is the Law of Equipartition of Energy?

The Law of Equipartition of Energy states that, at thermal equilibrium, the total energy of a system is distributed equally among all degrees of freedom, with each degree of freedom contributing an average energy of $\frac{1}{2} k_B T$ , where $k_B$ is the Boltzmann constant and $T$ is the absolute temperature of the system. The law is applicable to systems in which energy can be stored in different forms, such as translational, rotational, and vibrational energy.

Key Terms and Concepts

1. Degree of Freedom: A degree of freedom represents an independent way in which a particle can move or store energy. For example, in a three-dimensional system, a particle can move along the x, y, and z axes, giving it three translational degrees of freedom. Complex molecules may have additional rotational and vibrational degrees of freedom.

2. Boltzmann Constant ( $k_B$ ): The Boltzmann constant is a fundamental physical constant that relates the average kinetic energy of particles in a gas to temperature. Its value is approximately $1.38 \times 10^{-23} \, \text{J/K}$ .

3. Thermal Equilibrium: Thermal equilibrium refers to a state in which all parts of a system have the same temperature, allowing energy to be evenly distributed.

The Law of Equipartition of Energy is grounded in the assumption that each degree of freedom is independent and equally probable, allowing energy to be shared among them based solely on temperature.

Mathematical Formulation of the Law of Equipartition of Energy

The law is often expressed mathematically as follows:

$\langle E \rangle = \frac{1}{2} k_B T$

where:

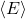$\langle E \rangle$ is the average energy associated with each degree of freedom,
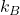$k_B$ is the Boltzmann constant,
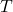$T$ is the temperature in kelvin (K).

For a system with $N$ degrees of freedom, the total average energy $E_{\text{total}}$ is given by:

$E_{\text{total}} = \frac{N}{2} k_B T$

This formula shows that the total energy of the system is directly proportional to the temperature and the number of degrees of freedom. Each degree of freedom contributes an average energy of $\frac{1}{2} k_B T$ , resulting in the total energy being distributed evenly across all degrees of freedom.

Translational, Rotational, and Vibrational Degrees of Freedom

1. Translational Degrees of Freedom: A particle moving in three-dimensional space has three translational degrees of freedom—one for each spatial dimension (x, y, and z). For an ideal gas, each translational degree of freedom contributes $\frac{1}{2} k_B T$ to the energy, giving a total translational energy of:

$E_{\text{trans}} = \frac{3}{2} k_B T$

2. Rotational Degrees of Freedom: Molecules with a complex structure can rotate around different axes, adding rotational degrees of freedom. Diatomic molecules have two rotational degrees of freedom (rotation around two perpendicular axes), while polyatomic molecules may have three. Each rotational degree of freedom contributes $\frac{1}{2} k_B T$ to the total energy. For example, a diatomic molecule has:

$E_{\text{rot}} = \frac{2}{2} k_B T = k_B T$

3. Vibrational Degrees of Freedom: Vibrational modes involve both kinetic and potential energy contributions, with each vibrational mode contributing $k_B T$ (i.e., $\frac{1}{2} k_B T$ for kinetic energy and $\frac{1}{2} k_B T$ for potential energy) to the total energy.

For example, a diatomic molecule with one vibrational mode has an average vibrational energy of:

$E_{\text{vib}} = k_B T$

Thus, for molecules with different types of motion, the total energy is the sum of the contributions from each degree of freedom.

Examples of Equipartition of Energy

To better understand how the Law of Equipartition of Energy operates in real systems, let’s look at some specific examples.

Example 1: Energy in an Ideal Gas

In an ideal gas, each particle has three translational degrees of freedom, corresponding to motion along the x, y, and z axes. According to the Law of Equipartition of Energy, each degree of freedom contributes $\frac{1}{2} k_B T$ to the total energy. For a single gas particle, the total energy is:

$E = \frac{3}{2} k_B T$

For a mole of gas particles, we multiply by Avogadro’s number $N_A$ to find the total energy $E_{\text{total}}$ :

$E_{\text{total}} = \frac{3}{2} N_A k_B T = \frac{3}{2} R T$

where $R = N_A k_B$ is the universal gas constant. This formula shows that the energy of an ideal gas depends only on temperature, making it directly proportional to $T$ .

Example 2: Energy Distribution in a Diatomic Molecule

Diatomic molecules, such as $\text{O}_2$ and $\text{N}_2$ , have additional rotational and vibrational degrees of freedom. A diatomic molecule can rotate around two perpendicular axes and vibrate along the bond axis, giving it five total degrees of freedom at moderate temperatures (three translational, two rotational).

The average energy for a diatomic molecule, ignoring vibrational modes at lower temperatures, is:

$E = \left( \frac{3}{2} + 1 \right) k_B T = \frac{5}{2} k_B T$

If we consider vibrational modes at higher temperatures, the energy would further increase as vibrational degrees of freedom begin to contribute.

Example 3: Equipartition in a Polyatomic Molecule

Polyatomic molecules, such as water ( $\text{H}_2\text{O}$ ) or carbon dioxide ( $\text{CO}_2$ ), have more complex structures, allowing them to rotate around three axes and vibrate in multiple modes. For a nonlinear polyatomic molecule, the degrees of freedom are distributed as follows:

3 translational degrees of freedom
3 rotational degrees of freedom (rotation around each axis in three-dimensional space)
Multiple vibrational degrees of freedom, depending on the molecule’s atomic structure

For example, for a nonlinear polyatomic molecule without considering vibrations, the average energy would be:

$E = \left( \frac{3}{2} + \frac{3}{2} \right) k_B T = 3 k_B T$

At higher temperatures, the vibrational modes would contribute additional energy, as each vibrational mode adds $k_B T$ to the total energy.

Applications of the Law of Equipartition of Energy

The Law of Equipartition of Energy has numerous applications in fields such as thermodynamics, molecular physics, and statistical mechanics. Below are some key applications:

1. Heat Capacity of Gases

The heat capacity of a substance is a measure of the amount of heat energy required to raise its temperature. The Law of Equipartition of Energy helps explain the heat capacities of gases. For instance, the molar heat capacity at constant volume ( $C_V$ ) for an ideal monoatomic gas is:

$C_V = \frac{3}{2} R$

where $R$ is the universal gas constant. For a diatomic gas, which has additional rotational degrees of freedom, the molar heat capacity is:

$C_V = \frac{5}{2} R$

At higher temperatures, where vibrational modes become active, the heat capacity increases further due to the added energy storage.

2. Understanding Molecular Motion in Liquids and Solids

In solids and liquids, atoms and molecules are constrained by intermolecular forces, but they still exhibit vibrational motion around their equilibrium positions. The Law of Equipartition of Energy applies here as well, with each vibrational degree of freedom contributing $k_B T$ to the total energy.

For example, in a solid crystal lattice, each atom vibrates in three-dimensional space, contributing to the material’s thermal energy. By

understanding this energy distribution, scientists can predict the behavior of materials under different thermal conditions.

3. Maxwell-Boltzmann Distribution in Kinetic Theory of Gases

The Law of Equipartition of Energy underlies the Maxwell-Boltzmann distribution, which describes the distribution of speeds among particles in a gas. According to this distribution, the average kinetic energy of a particle in a gas is $\frac{3}{2} k_B T$ , consistent with the Law of Equipartition of Energy.

This distribution is critical in predicting how gas particles behave at various temperatures, including properties like pressure and temperature, which are vital for understanding real-world gas behavior and applications in engine design and aerodynamics.

4. Blackbody Radiation and Quantum Mechanics

The Law of Equipartition of Energy was historically used to explain energy distribution in thermal systems. However, deviations from the law, observed in the energy distribution of blackbody radiation at low temperatures, led to the development of quantum mechanics. Max Planck’s work on blackbody radiation revealed that energy is quantized, resolving discrepancies that classical equipartition could not explain. This finding laid the foundation for quantum theory, which redefined energy distribution in microscopic systems.

Limitations of the Law of Equipartition of Energy

While the Law of Equipartition of Energy provides a valuable framework for understanding energy distribution, it has limitations:

1. Failure at Low Temperatures: At low temperatures, thermal energy may be insufficient to activate certain degrees of freedom, particularly vibrational modes. As a result, the law does not accurately predict the energy distribution, and quantum mechanical effects become significant.

2. Breakdown for Quantum Systems: Equipartition assumes that energy is continuously distributed among all degrees of freedom. In quantum systems, however, energy is quantized, and only specific energy levels are allowed. This quantization means that energy distribution does not always follow classical equipartition, especially in microscopic systems like atoms and molecules.

3. Inapplicability to Non-Equilibrium Systems: Equipartition applies only to systems in thermal equilibrium. Non-equilibrium systems, where temperature or energy varies across the system, require more complex models to describe their energy distribution.

Conclusion

The Law of Equipartition of Energy is a cornerstone of classical thermodynamics and statistical mechanics, providing a framework for understanding how energy is distributed among particles in a system. It allows us to calculate the energy associated with each degree of freedom and apply this knowledge to predict properties such as heat capacity, molecular motion, and kinetic energy in gases. While the law has limitations—particularly when dealing with quantum systems and low temperatures—it remains a valuable tool for understanding energy distribution in macroscopic systems. By exploring the applications and limitations of equipartition, we gain insight into the fundamental principles governing molecular and atomic behavior in physical systems.