Trigonometry Table: Understanding Angles and Ratios

Trigonometry, the branch of mathematics that studies the relationships between angles and sides of triangles, plays a vital role in various fields, including physics, engineering, architecture, and navigation. At its heart lies the trigonometry table, a systematic way of representing the values of trigonometric ratios for standard angles. This table simplifies complex calculations and serves as a valuable reference for solving problems. In this article, we will explore the structure of the trigonometry table, explain its significance, and illustrate its use through practical examples.

What Is a Trigonometry Table?

A trigonometry table provides the values of six fundamental trigonometric ratios—sine ( $\sin$ ), cosine ( $\cos$ ), tangent ( $\tan$ ), cosecant ( $\csc$ ), secant ( $\sec$ ), and cotangent ( $\cot$ )—for standard angles commonly used in trigonometry. These angles include $0^\circ, 30^\circ, 45^\circ, 60^\circ,$ and $90^\circ$ .

The Six Trigonometric Ratios:

1. Sine ( $\sin$ ): The ratio of the opposite side to the hypotenuse in a right triangle.

$\sin \theta = \frac{\text{Opposite}}{\text{Hypotenuse}}$

2. Cosine ( $\cos$ ): The ratio of the adjacent side to the hypotenuse.

$\cos \theta = \frac{\text{Adjacent}}{\text{Hypotenuse}}$

3. Tangent ( $\tan$ ): The ratio of the opposite side to the adjacent side.

$\tan \theta = \frac{\text{Opposite}}{\text{Adjacent}}$

4. Cosecant ( $\csc$ ): The reciprocal of sine.

$\csc \theta = \frac{1}{\sin \theta} = \frac{\text{Hypotenuse}}{\text{Opposite}}$

5. Secant ( $\sec$ ): The reciprocal of cosine.

$\sec \theta = \frac{1}{\cos \theta} = \frac{\text{Hypotenuse}}{\text{Adjacent}}$

6. Cotangent ( $\cot$ ): The reciprocal of tangent.

$\cot \theta = \frac{1}{\tan \theta} = \frac{\text{Adjacent}}{\text{Opposite}}$

The trigonometry table lists these values for specific angles to make solving trigonometric problems easier.

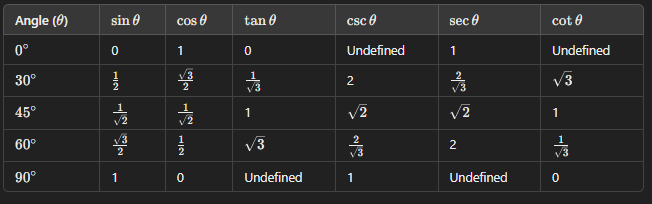
The Standard Trigonometry Table

Below is the trigonometry table for 0∘,30∘,45∘,60∘ and 90∘:

Deriving the Trigonometry Table

The values in the trigonometry table are derived using the geometry of a right triangle and the Pythagorean theorem. For standard angles like $30^\circ, 45^\circ,$ and $60^\circ$ , special triangles such as the 30-60-90 and 45-45-90 triangles are used.

1. 30-60-90 Triangle

In a 30-60-90 triangle, the side ratios are:

Shortest side (opposite $30^\circ$ ): $1$
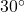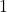
Hypotenuse: $2$
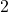
Longer side (opposite $60^\circ$ ): $\sqrt{3}$

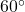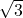
Using these ratios:

$\sin 30^\circ = \frac{1}{2},\ \cos 30^\circ = \frac{\sqrt{3}}{2},\ \tan 30^\circ = \frac{1}{\sqrt{3}}$
$\sin 60^\circ = \frac{\sqrt{3}}{2},\ \cos 60^\circ = \frac{1}{2},\ \tan 60^\circ = \sqrt{3}$

2. 45-45-90 Triangle

In a 45-45-90 triangle, the side ratios are:

Both legs: $1$
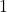
Hypotenuse: $\sqrt{2}$

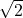
Using these ratios:

$\sin 45^\circ = \cos 45^\circ = \frac{1}{\sqrt{2}},\ \tan 45^\circ = 1$

Using the Trigonometry Table

The trigonometry table is a powerful tool for solving problems in geometry, physics, and engineering. Let’s explore some examples.

Example 1: Finding the Height of a Tower

A person stands 50 meters away from a tower and observes the top at an angle of $30^\circ$ . Find the height of the tower.

Solution:

From the right triangle:

$\tan 30^\circ = \frac{\text{Height of tower (opposite)}}{\text{Distance from tower (adjacent)}}$

From the table:

$\tan 30^\circ = \frac{1}{\sqrt{3}}$

Substitute the values:

$\frac{1}{\sqrt{3}} = \frac{\text{Height}}{50}$

Solve for height:

$\text{Height} = \frac{50}{\sqrt{3}} \approx 28.87 \, \text{meters}$

Example 2: Calculating the Length of a Ramp

A ramp makes an angle of $45^\circ$ with the ground and reaches a platform 5 meters high. Find the length of the ramp.

Solution:

Using:

$\sin \theta = \frac{\text{Height}}{\text{Length of ramp}}$

From the table:

$\sin 45^\circ = \frac{1}{\sqrt{2}}$

Substitute the values:

$\frac{1}{\sqrt{2}} = \frac{5}{\text{Length}}$

Solve for length:

$\text{Length} = 5 \sqrt{2} \approx 7.07 \, \text{meters}$

Example 3: Verifying Trigonometric Identities

Prove the identity:

$\sin^2 45^\circ + \cos^2 45^\circ = 1$

Solution:

From the table:

$\sin 45^\circ = \cos 45^\circ = \frac{1}{\sqrt{2}}$

Substitute the values:

$\left(\frac{1}{\sqrt{2}}\right)^2 + \left(\frac{1}{\sqrt{2}}\right)^2 = \frac{1}{2} + \frac{1}{2} = 1$

Identity verified.

Applications of the Trigonometry Table

1. Engineering and Construction

Engineers use the trigonometry table to calculate angles and distances when designing buildings, bridges, and machinery.

2. Navigation

Navigators rely on trigonometric tables to compute distances and angles when plotting courses, especially in aviation and maritime contexts.

3. Physics

In physics, trigonometric tables help resolve vector components, analyze waves, and calculate forces acting at angles.

Conclusion

The trigonometry table is an essential mathematical tool for understanding and applying trigonometric ratios. By providing ready-made values for standard angles, it simplifies calculations in various fields, from

architecture to science. Mastering the trigonometry table not only strengthens mathematical skills but also enhances problem-solving abilities in real-world applications. Whether calculating the height of a building, the length of a ramp, or resolving forces, the trigonometry table is an invaluable resource.