Understanding Angular Displacement: Concepts, Formula, and Applications

Angular displacement is a fundamental concept in rotational motion that describes the angle through which an object rotates about a fixed axis over time. It measures how much an object has rotated from its starting position and is an essential parameter in physics and engineering for understanding rotational movement in wheels, gears, celestial bodies, and many other systems. Angular displacement is closely related to angular velocity and angular acceleration, making it a cornerstone of rotational kinematics and dynamics.

In this article, we’ll explore the concept of angular displacement, discuss its formula, and look at its applications with examples to illustrate how it is used in real-life situations.

What is Angular Displacement?

Angular displacement is defined as the angle through which an object rotates about a specific point or axis. It is a vector quantity, meaning it has both magnitude and direction. The direction of angular displacement is determined by the rotation’s sense—either clockwise or counterclockwise—and is usually measured in radians ( $\text{rad}$ ) or degrees ( $°$ ).

Unlike linear displacement, which measures the shortest distance between an initial and final position, angular displacement measures the angle covered by a rotating object over a particular period.

Formula for Angular Displacement

The angular displacement ( $\theta$ ) of an object rotating around a fixed axis is given by the formula:

$\theta = \frac{s}{r}$

where:

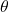$\theta$ = angular displacement (in radians),
$s$ = arc length traveled by the rotating object (in meters),
$r$ = radius of the circular path (in meters).

Since the arc length $s$ represents the actual path traveled, dividing it by the radius $r$ yields the angular displacement in radians. One full revolution around a circular path corresponds to an angular displacement of $2\pi$ radians (or 360°).

Understanding Angular Displacement as a Vector

Angular displacement is considered a vector quantity because it has both magnitude and direction. Its direction follows the right-hand rule: if you curl your right hand’s fingers in the direction of rotation, your thumb points in the direction of the angular displacement vector. Conventionally, counterclockwise rotation is taken as positive, while clockwise rotation is negative.

Units of Angular Displacement

Angular displacement is commonly measured in the following units:

1. Radians (rad): The radian is the standard unit for angular displacement in physics. One radian is the angle formed when the arc length equals the radius. For a complete circle, the angular displacement is $2\pi$ radians.

2. Degrees (°): Angular displacement can also be measured in degrees, where one full rotation is 360°. To convert between radians and degrees, use the following relationships:
– $1 \, \text{rad} = \frac{180}{\pi} \, \text{degrees}$
– $1 \, \text{degree} = \frac{\pi}{180} \, \text{rad}$

Example: An angular displacement of $\pi$ radians is equivalent to 180°, and $\frac{\pi}{2}$ radians is equivalent to 90°.

Relationship Between Angular Displacement and Linear Displacement

Angular displacement is related to the linear displacement (arc length) along a circular path. This relationship is useful when dealing with objects in circular motion. The arc length $s$ is given by:

$s = r \cdot \theta$

where:

$s$ = arc length,
$r$ = radius of the circular path,
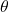$\theta$ = angular displacement (in radians).

This equation shows that for a given radius, the linear distance an object travels along a circular path is directly proportional to its angular displacement. Thus, for a larger radius, a greater linear displacement is achieved for the same angular displacement.

Example: Relationship Between Angular and Linear Displacement

Consider a wheel with a radius of $0.5 \, \text{m}$ that rotates through an angular displacement of $\pi$ radians. To find the arc length (linear displacement) covered by a point on the edge of the wheel, use the formula:

$s = r \cdot \theta = 0.5 \, \text{m} \times \pi = 1.57 \, \text{m}$

This means that a point on the edge of the wheel travels 1.57 meters along the circular path as the wheel rotates through $\pi$ radians.

Calculating Angular Displacement in Terms of Angular Velocity and Time

If the angular velocity ( $\omega$ ) of an object is constant, angular displacement can be calculated as the product of angular velocity and time:

$\theta = \omega \cdot t$

where:

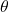$\theta$ = angular displacement (in radians),
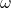$\omega$ = angular velocity (in radians per second),
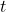$t$ = time (in seconds).

This relationship is similar to the formula for linear displacement, where displacement equals velocity multiplied by time.

Example: If a fan blade rotates with an angular velocity of $2 \, \text{rad/s}$ for 10 seconds, the angular displacement can be calculated as:

$\theta = \omega \cdot t = 2 \, \text{rad/s} \times 10 \, \text{s} = 20 \, \text{rad}$

This means that over 10 seconds, the fan blade undergoes an angular displacement of 20 radians.

Applications of Angular Displacement

Angular displacement plays a significant role in various real-life applications, particularly those involving rotational or circular motion. Here are some key areas where angular displacement is a critical factor:

1. Wheels and Rotational Motion in Vehicles

In vehicles like cars and bicycles, wheels undergo angular displacement as they rotate, allowing the vehicle to move forward. The relationship between angular and linear displacement helps engineers determine the distance traveled by the vehicle based on the rotation of its wheels.

Example: Suppose a car’s tire has a radius of 0.3 meters, and it rotates through an angular displacement of $10 \pi$ radians. To find the distance the car travels, calculate the arc length:

$s = r \cdot \theta = 0.3 \, \text{m} \times 10\pi = 3\pi \approx 9.42 \, \text{m}$

This means the car travels a linear distance of approximately 9.42 meters as the wheel undergoes this angular displacement.

2. Gears and Machinery

Angular displacement is crucial in the design and function of gears, where rotational motion is transmitted from one gear to another. The angular displacement of each gear determines the speed and direction of motion in mechanical systems like engines, clocks, and industrial machinery.

Example: In a clock, the minute hand and hour hand rotate with different angular displacements. The minute hand completes one full rotation (360° or $2\pi$ radians) every hour, while the hour hand completes one rotation in 12 hours. Understanding angular displacement allows for precise timing and synchronization.

3. Rotational Kinematics in Sports

In sports like gymnastics, figure skating, and diving, athletes perform rotations and spins where angular displacement is a key measure of their movements. For example, a gymnast’s spin or a diver’s somersault can be quantified in terms of angular displacement, allowing coaches and athletes to improve performance.

Example: A figure skater who completes three full spins during a routine has undergone an angular displacement of $3 \times 2\pi = 6\pi$ radians, or approximately 18.85 radians. This measurement provides a quantifiable measure of the skater’s rotational skill.

4. Robotics and Mechanical Arms

Angular displacement is vital in robotics and the design of robotic arms, where each joint undergoes controlled rotations to perform tasks with precision. The angles and rotations required to move each segment of the arm can be calculated using angular displacement principles.

Example: A robotic arm in a manufacturing facility might need to rotate its joints by specific angles to assemble parts. For instance, if a joint needs to rotate by 90° (or $\frac{\pi}{2}$ radians) to pick up an object, calculating angular displacement ensures the arm reaches the correct position.

5. Planetary Motion and Astronomy

In astronomy, celestial bodies like planets and satellites move along circular or elliptical orbits, and their angular displacement describes their rotation around a central body. Understanding angular displacement is crucial in calculating orbital periods and predicting planetary positions.

Example: The Earth completes one full orbit around the Sun each year, resulting in an angular displacement of $2\pi$ radians. Tracking angular displacement allows astronomers to predict the position of planets over time.

6. Amusement Park Rides

Angular displacement is also essential in amusement park rides, where components rotate, spin, or move along circular paths. Engineers calculate angular displacement to ensure the safe design and operation of rides like Ferris wheels, carousels, and roller coasters.

Example: A Ferris wheel with a radius of 15 meters rotates through an angular displacement of $\pi$ radians (half a circle). The arc length traveled by a passenger is:

$s = r \cdot \theta = 15 \, \text{m} \times \pi = 47.1 \, \text{m}$

This information helps ensure the ride moves at a safe and enjoyable speed.

Key Points and Takeaways

The concept of angular

displacement offers insights into rotational motion and has applications across various fields. Here are some key takeaways:

1. Unit of Measurement: Angular displacement is commonly measured in radians, where one full rotation is $2\pi$ radians. Degrees can also be used but are less common in physics.
2. Vector Nature: Angular displacement is a vector, meaning it has both magnitude (angle) and direction (sense of rotation).
3. Relationship to Linear Displacement: Angular displacement is related to linear displacement through the radius of the rotation, providing a way to convert rotational motion to linear movement.
4. Applications in Technology: From vehicles to amusement park rides, angular displacement is critical in designing and controlling rotational systems, providing essential information for safe and precise operation.

Conclusion

Angular displacement is a fundamental concept in understanding and quantifying rotational motion. Defined as the angle an object rotates around a fixed axis, angular displacement is a vector quantity with a wide range of applications in engineering, robotics, sports, and astronomy. The formula $\theta = \frac{s}{r}$ relates angular displacement to arc length, allowing us to analyze circular motion and convert it into linear terms.

By understanding angular displacement, engineers, physicists, and other professionals can design, analyze, and control systems that involve rotation, from simple wheels to complex robotic arms and planetary orbits. The concept underscores the importance of rotational kinematics in both theoretical and practical fields, helping us explore, design, and harness the power of rotational motion across various disciplines.