Boltzmann’s constant (![]() ) is a fundamental physical constant that bridges the microscopic world of individual particles with the macroscopic properties of systems in thermodynamics and statistical mechanics. Named after Austrian physicist Ludwig Boltzmann, this constant plays a central role in describing the relationship between temperature, energy, and entropy in a system.
) is a fundamental physical constant that bridges the microscopic world of individual particles with the macroscopic properties of systems in thermodynamics and statistical mechanics. Named after Austrian physicist Ludwig Boltzmann, this constant plays a central role in describing the relationship between temperature, energy, and entropy in a system.

In this article, we’ll explore the significance, mathematical framework, and applications of Boltzmann’s constant, with examples to clarify each concept.
What Is Boltzmann’s Constant?
Boltzmann’s constant (![]() ) relates the average kinetic energy of particles in a gas to the temperature of the system. It serves as a scaling factor that connects the microscopic behavior of particles to macroscopic thermodynamic quantities.
) relates the average kinetic energy of particles in a gas to the temperature of the system. It serves as a scaling factor that connects the microscopic behavior of particles to macroscopic thermodynamic quantities.
The value of Boltzmann’s constant is:
![]()
Where:
 is Boltzmann’s constant.
is Boltzmann’s constant.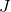 is joules, the unit of energy.
is joules, the unit of energy.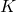 is kelvin, the unit of temperature.
is kelvin, the unit of temperature.
Key Insight
Boltzmann’s constant essentially defines the amount of energy per particle per unit temperature, making it a cornerstone in understanding thermal physics.
Example: In a gas at a temperature of 300 K, the average kinetic energy per molecule is proportional to ![]() , where
, where ![]() is the temperature in kelvins.
is the temperature in kelvins.
—
Boltzmann’s Constant in the Kinetic Theory of Gases
The kinetic theory of gases describes the behavior of gas particles based on their motion and interactions. Boltzmann’s constant plays a pivotal role in linking temperature to the average kinetic energy of gas particles.
Average Kinetic Energy of a Gas Particle
The average kinetic energy (![]() ) of a single particle in an ideal gas is given by:
) of a single particle in an ideal gas is given by:
![]()
Where:
 is Boltzmann’s constant.
is Boltzmann’s constant.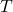 is the temperature in kelvins.
is the temperature in kelvins.
Example: For a gas at ![]() :
:
![]()
This energy represents the average kinetic energy of each molecule in the gas.
Implications in Gases
Boltzmann’s constant provides a direct way to calculate microscopic energy levels from macroscopic temperature, enabling a deeper understanding of thermal energy distribution among gas particles.
—
Boltzmann’s Constant and Entropy
Entropy (![]() ) is a measure of disorder or randomness in a system. Boltzmann’s constant appears in Boltzmann’s entropy formula:
) is a measure of disorder or randomness in a system. Boltzmann’s constant appears in Boltzmann’s entropy formula:
![]()
Where:
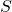 is the entropy of the system.
is the entropy of the system.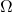 is the number of microstates (possible configurations of particles in the system).
is the number of microstates (possible configurations of particles in the system).
Significance of the Formula
Boltzmann’s entropy formula connects the microscopic details of a system (![]() ) with the macroscopic thermodynamic property of entropy (
) with the macroscopic thermodynamic property of entropy (![]() ).
).
Example: Consider a system with ![]() microstates. The entropy is:
microstates. The entropy is:
![]()
This demonstrates how Boltzmann’s constant relates microscopic configurations to observable thermodynamic properties.
—
Boltzmann Distribution and Thermal Equilibrium
Boltzmann’s constant is critical in the Boltzmann distribution, which describes the probability of a system being in a particular energy state at thermal equilibrium. The probability (![]() ) of a system being in a state with energy
) of a system being in a state with energy ![]() is given by:
is given by:
![]()
Where:
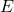 is the energy of the state.
is the energy of the state.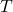 is the temperature.
is the temperature.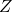 is the partition function, a normalization factor.
is the partition function, a normalization factor.
Example: Molecular Energy Levels
Consider a molecule with energy levels ![]() and
and ![]() at
at ![]() . The probabilities of these levels are:
. The probabilities of these levels are:
![]()
Calculating the exponent:
![]()
Thus:
![]()
The relative probability of being in ![]() versus
versus ![]() is significantly lower, emphasizing that higher-energy states are less likely at lower temperatures.
is significantly lower, emphasizing that higher-energy states are less likely at lower temperatures.
—
Applications of Boltzmann’s Constant
Boltzmann’s constant is foundational in many areas of physics and engineering. Here are some key applications:
1. Blackbody Radiation
Boltzmann’s constant appears in Planck’s law, which describes the intensity of radiation emitted by a blackbody as a function of wavelength and temperature. The Stefan-Boltzmann law, derived from this, states:
![]()
Where:
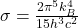 is the Stefan-Boltzmann constant.
is the Stefan-Boltzmann constant.
Example: The radiant power of the Sun, with a surface temperature of approximately ![]() , is calculated using this law.
, is calculated using this law.
—
2. Ideal Gas Law
Boltzmann’s constant links the microscopic and macroscopic forms of the ideal gas law:
![]()
Where:
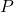 is pressure.
is pressure.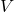 is volume.
is volume.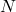 is the number of particles.
is the number of particles. connects the macroscopic gas constant (
connects the macroscopic gas constant (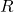 ) via
) via 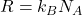 , where
, where  is Avogadro’s number.
is Avogadro’s number.
Example: For 1 mole of gas (![]() ) at
) at ![]() and
and ![]() , the volume is:
, the volume is:
![]()
—
3. Noise in Electronic Circuits
Boltzmann’s constant appears in the formula for thermal noise, or Johnson-Nyquist noise, in resistors:
![]()
Where:
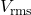 is the root-mean-square voltage.
is the root-mean-square voltage.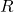 is resistance.
is resistance.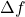 is the bandwidth.
is the bandwidth.
Example: For a ![]() resistor at
resistor at ![]() over a
over a ![]() bandwidth:
bandwidth:
![]()
—
4. Semiconductor Physics
In semiconductors, Boltzmann’s constant is used to describe carrier distributions. The Fermi-Dirac distribution depends on ![]() :
:
![]()
Example: Calculating the probability of electron occupation in conduction bands at a given temperature requires ![]() .
.
—
Boltzmann’s Constant in Modern Physics
Boltzmann’s constant is critical in quantum mechanics and cosmology. It sets the scale for the Planck temperature, the upper limit of thermodynamic temperature in the universe.
—
Conclusion
Boltzmann’s constant is a cornerstone of modern physics, linking the microscopic world of particles to macroscopic thermodynamic properties. It plays a central role in describing energy distributions, entropy, and thermal behavior in various systems. From the kinetic energy of gas molecules to blackbody radiation and semiconductor physics, Boltzmann’s constant enables scientists and engineers to connect theory with real-world phenomena. Its applications continue to expand, providing deeper insights into the workings of the universe.