Understanding Buoyancy: Definition, Principles, and Applications

Buoyancy is the force that allows objects to float in a fluid, such as water or air. This force occurs due to differences in fluid pressure acting on various parts of an object when it is immersed in a fluid. Buoyancy plays a critical role in a wide range of natural and engineered systems, from floating ships and hot air balloons to the survival of aquatic life. The concept of buoyancy is governed by Archimedes’ Principle, which provides the basis for understanding why and how objects float or sink.

In this article, we’ll dive into the fundamentals of buoyancy, including its definition, underlying principles, calculations, and real-world applications.

What is Buoyancy?

Buoyancy is an upward force exerted by a fluid that opposes the weight of an object immersed in it. When an object is placed in a fluid, the fluid exerts pressure on all surfaces of the object. The pressure exerted on the bottom of the object is greater than the pressure exerted on the top due to the weight of the fluid above. This difference in pressure results in a net upward force, or buoyant force, on the object.

Archimedes’ Principle

The principle of buoyancy was discovered by the ancient Greek mathematician Archimedes and is known as Archimedes’ Principle. Archimedes’ Principle states:

*The buoyant force acting on an object immersed in a fluid is equal to the weight of the fluid displaced by the object.*

This means that if an object displaces a certain volume of fluid, the fluid’s weight corresponds to the buoyant force experienced by the object. If this buoyant force is greater than or equal to the weight of the object, the object will float; if it is less, the object will sink.

Mathematical Expression of Buoyancy

The buoyant force ( $F_b$ ) acting on an object can be calculated as follows:

$F_b = \rho \times V \times g$

where:

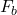$F_b$ is the buoyant force,
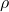$\rho$ is the density of the fluid,
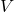$V$ is the volume of the fluid displaced by the object,
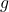$g$ is the acceleration due to gravity (approximately 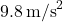$9.8 \, \text{m/s}^2$ on Earth).

This formula shows that buoyancy depends on the density of the fluid, the volume of fluid displaced, and gravitational force.

Example of Calculating Buoyant Force

Consider a solid block of wood with a volume of $0.5 \, \text{m}^3$ floating in water. The density of water is $1000 \, \text{kg/m}^3$ . Using the buoyancy formula:

$F_b = \rho \times V \times g$

$F_b = 1000 \times 0.5 \times 9.8 = 4900 \, \text{N}$

The buoyant force acting on the block is $4900 \, \text{N}$ .

Factors Affecting Buoyancy

Several factors influence buoyancy, including the density of the object and fluid, the volume of the displaced fluid, and the gravitational force. Let’s explore these factors and how they determine whether an object will float or sink.

1. Density of the Object and the Fluid

The density of an object relative to the density of the fluid determines its buoyancy. If the density of the object is less than the density of the fluid, it will float; if it is greater, it will sink. This is why ice, with a density lower than water, floats, whereas rocks, which are denser than water, sink.

Example: An ice cube has a density of about $920 \, \text{kg/m}^3$ , which is less than the density of water ( $1000 \, \text{kg/m}^3$ ). As a result, ice floats in water because the buoyant force exerted by the water exceeds the weight of the ice.

2. Volume of Displaced Fluid

The amount of fluid displaced by an object directly affects the buoyant force. Larger objects displace more fluid, resulting in a higher buoyant force. Therefore, objects with larger volumes have a greater tendency to float, even if they have the same density as smaller objects.

Example: Large steel ships float because they displace enough water to generate a buoyant force that balances their weight, even though steel is denser than water.

3. Gravitational Force

Buoyancy is influenced by gravity, as it affects both the weight of the displaced fluid and the weight of the object. A higher gravitational force will increase both the weight and the buoyant force proportionally, but this will not affect the floating or sinking behavior of an object in a given fluid.

Example: In a reduced-gravity environment, such as on the Moon, the buoyant force acting on an object would decrease since gravity is weaker there. However, an object’s tendency to float or sink in a given fluid would remain the same as on Earth, since both weight and buoyant force scale down together.

Types of Buoyancy

Buoyancy can be classified based on the object’s behavior in the fluid. There are three main types of buoyancy:

1. Positive Buoyancy

An object experiences positive buoyancy if it floats on the surface of a fluid. This happens when the buoyant force is greater than the weight of the object. Objects with lower density than the fluid will have positive buoyancy.

Example: A rubber ball dropped in water floats due to positive buoyancy. The density of rubber is lower than that of water, so the buoyant force is greater than the weight of the ball.

2. Neutral Buoyancy

An object has neutral buoyancy when it remains suspended within the fluid without sinking or floating. In this case, the weight of the object equals the buoyant force. Scuba divers often achieve neutral buoyancy to remain suspended in water without floating upward or sinking.

Example: A fish achieves neutral buoyancy by adjusting the air in its swim bladder. This balance allows the fish to stay at a specific depth in water without exerting additional effort.

3. Negative Buoyancy

An object exhibits negative buoyancy when it sinks in a fluid. This occurs when the weight of the object is greater than the buoyant force acting on it, usually because the object’s density is higher than the fluid’s density.

Example: A metal coin dropped into water will sink because its density is much higher than that of water, resulting in a weight that exceeds the buoyant force.

Applications of Buoyancy

Buoyancy is a fundamental concept with diverse applications in fields like engineering, transportation, medicine, and environmental science. Below are some examples of how buoyancy principles are applied in real life.

1. Ship and Boat Design

Buoyancy is critical in designing ships and boats, as it determines whether a vessel will float or sink. Designers create hulls with large volumes and low densities to displace enough water and generate sufficient buoyant force. This allows massive ships, including cargo vessels and cruise liners, to float despite their heavy loads.

Example: A steel ship has a hollow hull, which increases the volume of water it displaces, generating a buoyant force that counterbalances its weight. Although steel is denser than water, the large volume of the hull ensures positive buoyancy.

2. Submarines and Underwater Exploration

Submarines control their buoyancy by adjusting their ballast tanks, which can be filled with either water or air. When the tanks are filled with water, the submarine’s density increases, causing it to sink. When the tanks are filled with air, its density decreases, and it rises to the surface. This control allows submarines to dive, hover at specific depths, or surface as needed.

Example: A submarine descends by allowing water into its ballast tanks, increasing its overall density and creating negative buoyancy. When the submarine needs to ascend, it pumps air into the tanks, reducing density and creating positive buoyancy.

3. Hot Air Balloons

Buoyancy also applies to gases, as seen in hot air balloons. When air inside the balloon is heated, it becomes less dense than the cooler air outside. This difference in density creates a buoyant force that lifts the balloon. The balloon descends when the air inside cools and becomes denser.

Example: To rise, a hot air balloon operator heats the air within the balloon, reducing its density relative to the cooler air outside. This buoyant force overcomes the balloon’s weight, lifting it into the sky.

4. Scuba Diving

Scuba divers use buoyancy control devices (BCDs) to manage their buoyancy underwater. By adjusting the amount of air in the BCD, divers can increase or decrease their volume, achieving neutral, positive, or negative buoyancy to move easily through different water depths.

Example: A diver adds air to the BCD to increase buoyancy when ascending and releases air to reduce buoyancy when descending. This control allows the diver to maintain stable positioning underwater.

5. Fish Swim Bladders

Fish possess an internal organ called a swim bladder, which they use to control their buoyancy. By adjusting the amount of gas in the swim bladder, fish can remain neutrally buoyant and hover at specific depths without using energy. This natural mechanism allows fish to move efficiently in water.

Example: When a fish adds gas to its swim bladder, it increases its buoyancy, allowing it to rise in the water column. To sink, the fish releases gas from the

bladder, decreasing buoyancy.

6. Weather and Meteorology

Buoyancy affects weather patterns and atmospheric conditions. Warm air rises because it is less dense than cold air, leading to cloud formation and weather systems. Atmospheric buoyancy is essential in understanding phenomena like convection currents, thunderstorms, and wind patterns.

Example: During the day, the sun heats the ground, warming the air above it. This warm air, being less dense, rises and creates convection currents that can lead to cloud formation and, sometimes, precipitation.

Problem-Solving with Buoyancy: Example Calculations

To understand buoyancy calculations, let’s examine a sample problem.

Example Problem

A metal cube with a volume of $0.02 \, \text{m}^3$ is placed in water. The density of water is $1000 \, \text{kg/m}^3$ , and the density of the metal cube is $5000 \, \text{kg/m}^3$ . Will the cube float or sink?

Step 1: Calculate the weight of the metal cube.

$\text{Weight of cube} = \text{density} \times \text{volume} \times g$

$= 5000 \times 0.02 \times 9.8 = 980 \, \text{N}$

Step 2: Calculate the buoyant force.

$F_b = \rho \times V \times g$

$= 1000 \times 0.02 \times 9.8 = 196 \, \text{N}$

Since the weight of the metal cube (980 N) is greater than the buoyant force (196 N), the cube will sink.

Conclusion

Buoyancy is a fundamental force that governs the behavior of objects in fluids, whether it’s a boat floating on water, a fish controlling its depth, or a hot air balloon rising in the sky. Archimedes’ Principle provides the basis for understanding buoyancy, allowing us to predict whether an object will float or sink based on its density and volume of displaced fluid.

From engineering applications like ship design and submarine control to natural phenomena in weather patterns and animal physiology, buoyancy plays a crucial role in shaping the world around us. Understanding how to calculate buoyant force and recognizing the factors that influence buoyancy allow us to harness this force in innovative ways, advancing both technology and science.