Understanding Capacitance: Concepts, Principles, and Applications

Capacitance is a fundamental concept in electrical engineering and physics, describing the ability of a system to store electric charge. Capacitors, the components that utilize capacitance, are essential in a wide range of applications, from energy storage and signal processing to power management and electronic circuits. By understanding capacitance, we can better analyze and design electrical and electronic systems.

This article provides an in-depth exploration of capacitance, its principles, mathematical expressions, types of capacitors, and practical applications, with examples to illustrate each concept.

What Is Capacitance?

Capacitance is the property of a system that allows it to store an electric charge when a potential difference (voltage) exists across its terminals. It is defined as the ratio of the electric charge ( $Q$ ) stored on the plates of the capacitor to the voltage ( $V$ ) across those plates:

$C = \frac{Q}{V}$

Where:

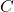$C$ is the capacitance, measured in farads (F).
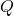$Q$ is the charge stored, measured in coulombs (C).
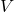$V$ is the voltage across the capacitor, measured in volts (V).

Key Features of Capacitance

1. Linear Relationship: In an ideal capacitor, the charge stored is directly proportional to the applied voltage.
2. Unit of Measurement: The farad (F) is the SI unit of capacitance, where 1 farad = 1 coulomb per volt. However, most practical capacitors have capacitances in microfarads (µF), nanofarads (nF), or picofarads (pF).

Example: A capacitor with a capacitance of $10 \, \mu F$ stores a charge of $50 \, \mu C$ when a $5 \, V$ voltage is applied. Using the formula $C = Q / V$ :

$C = \frac{50 \times 10^{-6}}{5} = 10 \times 10^{-6} \, \text{F} = 10 \, \mu F$

Structure and Working of a Capacitor

A capacitor is composed of two conductive plates separated by an insulating material called the dielectric. When voltage is applied across the plates, electric charge accumulates on the surfaces of the plates, creating an electric field.

How a Capacitor Works

1. Charging Phase:
– Electrons are removed from one plate, creating a positive charge.
– These electrons accumulate on the other plate, creating a negative charge.
– The electric field between the plates stores energy.

2. Discharging Phase:
– When the voltage source is removed and the capacitor is connected to a load, the stored charge flows through the circuit, releasing the stored energy.

Example: In a flashlight, the capacitor charges when the flashlight is off. When turned on, the capacitor discharges rapidly to provide a burst of energy to the light bulb.

Factors Affecting Capacitance

The capacitance of a capacitor depends on its physical and material properties:

1. Plate Area ( $A$ ):
– Larger plate areas allow more charge to be stored, increasing capacitance.
– Capacitance is directly proportional to the plate area.

2. Distance Between Plates ( $d$ ):
– A smaller separation between the plates results in stronger electric fields and higher capacitance.
– Capacitance is inversely proportional to the plate distance.

3. Dielectric Material:
– The dielectric increases capacitance by reducing the electric field strength, allowing more charge to be stored for a given voltage.
– The dielectric constant ( $\varepsilon_r$ ) of the material determines the capacitance.

The capacitance is calculated as:

$C = \varepsilon_r \varepsilon_0 \frac{A}{d}$

Where:

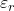$\varepsilon_r$ is the relative permittivity (dielectric constant).
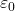$\varepsilon_0$ is the permittivity of free space ( $8.85 \times 10^{-12} \, \text{F/m}$ ).
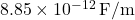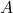$A$ is the plate area.
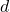$d$ is the distance between the plates.

Example: A capacitor with plate area $0.01 \, \text{m}^2$ , plate separation $1 \, \text{mm}$ , and a dielectric with $\varepsilon_r = 4$ has a capacitance:

$C = 4 \cdot 8.85 \times 10^{-12} \cdot \frac{0.01}{0.001} = 354 \, \text{pF}.$

Types of Capacitors

Capacitors come in various types, designed for specific applications:

1. Ceramic Capacitors

– Small, inexpensive, and widely used.
– Commonly used in high-frequency circuits and decoupling applications.

Example: Ceramic capacitors are found in smartphone circuit boards to stabilize voltage.

2. Electrolytic Capacitors

– High capacitance values.
– Used for energy storage, filtering, and smoothing in power supplies.

Example: Used in audio amplifiers to filter out low-frequency noise.

3. Film Capacitors

– Stable and reliable, with low energy loss.
– Used in signal processing and motor run circuits.

Example: Found in electric motors to improve efficiency.

4. Tantalum Capacitors

– Compact with high capacitance-to-volume ratios.
– Used in space-constrained applications like portable devices.

Example: Used in medical devices such as portable ECG machines.

5. Supercapacitors

– Extremely high capacitance values.
– Used for energy storage and backup power applications.

Example: Found in regenerative braking systems in electric vehicles.

Energy Stored in a Capacitor

A capacitor stores energy in the electric field between its plates. The energy ( $U$ ) stored is given by:

$U = \frac{1}{2} C V^2$

Example: A $100 \, \mu F$ capacitor charged to $10 \, V$ stores energy:

$U = \frac{1}{2} \cdot 100 \times 10^{-6} \cdot 10^2 = 0.05 \, \text{J}.$

Capacitors in Series and Parallel

Capacitors can be connected in series or parallel, and their equivalent capacitance depends on the configuration.

Capacitors in Series

The total capacitance ( $C_{\text{eq}}$ ) of capacitors in series is given by:

$\frac{1}{C_{\text{eq}}} = \frac{1}{C_1} + \frac{1}{C_2} + \dots$

Example: For two capacitors, $C_1 = 4 \, \mu F$ and $C_2 = 6 \, \mu F$ , in series:

$\frac{1}{C_{\text{eq}}} = \frac{1}{4} + \frac{1}{6} = \frac{5}{12}, \, C_{\text{eq}} = 2.4 \, \mu F.$

Capacitors in Parallel

The total capacitance of capacitors in parallel is the sum of their individual capacitances:

$C_{\text{eq}} = C_1 + C_2 + \dots$

Example: For $C_1 = 4 \, \mu F$ and $C_2 = 6 \, \mu F$ in parallel:

$C_{\text{eq}} = 4 + 6 = 10 \, \mu F.$

Applications of Capacitance

Capacitors are critical components in various technologies:

1. Energy Storage

– Capacitors store energy for use in power backup and energy harvesting.

Example: Supercapacitors in electric buses provide bursts of power for acceleration.

2. Filtering

– Capacitors remove unwanted signals in AC and DC circuits.

Example: Used in power supplies to filter out AC ripple in DC outputs.

3. Timing Circuits

– Capacitors work with resistors to create time delays in circuits.

Example: Found in camera flash units to create delay before firing.

4. Signal Coupling and Decoupling

– Used to pass AC signals while blocking DC components.

Example: In audio systems, capacitors separate audio signals from power supply noise.

5. Motor Starting and Running

– Capacitors provide phase shift for starting and running motors.

Example: Used in ceiling fans to ensure smooth startup.

Practical Considerations in Using Capacitors

1. Voltage Rating: Ensure the capacitor can handle the circuit voltage without breaking down.
2. Tolerance: Account for variations in capacitance values due to manufacturing limits.
3. Temperature Sensitivity: Some capacitors are sensitive to temperature changes, affecting performance.

Conclusion

Capacitance is a cornerstone of modern electronics, enabling the design and operation of countless devices and systems. By understanding its principles, structure, and behavior, we can harness capacitors for energy storage, signal processing, and power management.