Correlation is a statistical measure that describes the relationship or association between two variables. It helps determine whether an increase or decrease in one variable corresponds to an increase or decrease in another. Correlation is widely used in fields such as statistics, economics, psychology, and data science to help understand patterns in data, inform decision-making, and identify trends.
This article delves into the concept of correlation, the types of correlation, how it is measured, and what it signifies. We’ll also explore examples to see how correlation works in real-life scenarios and discuss some limitations and misconceptions about correlation.
What is Correlation?
Correlation quantifies the degree to which two variables move in relation to each other. If the variables tend to increase or decrease together, they are said to be positively correlated. If one variable tends to increase when the other decreases, they are negatively correlated. If the variables show no consistent relationship, they are said to have no correlation.
Key Points of Correlation:
- Correlation does not imply causation. It only suggests a relationship, not a cause-and-effect link.
- Correlation is represented by a correlation coefficient, a value that ranges from -1 to 1. A correlation coefficient close to 1 or -1 indicates a strong relationship, while a coefficient close to 0 indicates little or no relationship.
The most common measure of correlation is the Pearson correlation coefficient (r), which is used for linear relationships.
Correlation Coefficient Values and Interpretation:
- +1: Perfect positive correlation (variables move together perfectly in the same direction).
- -1: Perfect negative correlation (variables move together perfectly in opposite directions).
- 0: No correlation (no relationship between the variables).
Types of Correlation
There are different types of correlation, each describing a unique type of relationship between variables. The main types of correlation include positive correlation, negative correlation, and no correlation.
1. Positive Correlation
Positive correlation occurs when an increase in one variable is associated with an increase in the other, and vice versa. In other words, the variables move in the same direction.
Example of Positive Correlation:
Consider the relationship between education level and income. Studies have shown that as education level increases, income tends to increase as well. Here, education level and income have a positive correlation. People with higher levels of education often earn more, while those with lower levels of education tend to earn less.
2. Negative Correlation
Negative correlation describes a relationship in which an increase in one variable is associated with a decrease in the other, and vice versa. In other words, the variables move in opposite directions.
Example of Negative Correlation:
Consider the relationship between exercise frequency and body weight. Generally, as the frequency of exercise increases, body weight tends to decrease. This is a negative correlation because when one variable (exercise frequency) increases, the other (body weight) decreases.
3. No Correlation
No correlation means there is no relationship between two variables; changes in one variable do not affect the other. In this case, the correlation coefficient is close to 0.
Example of No Correlation:
Suppose we examine the relationship between shoe size and intelligence. These two variables likely have no correlation because there is no logical connection between a person’s shoe size and their intelligence.
Types Based on Strength of Correlation
Correlation can also be categorized by its strength:
- Strong correlation: Correlation coefficient is close to -1 or +1, indicating a strong relationship.
- Moderate correlation: Correlation coefficient is moderately close to -1 or +1.
- Weak correlation: Correlation coefficient is close to 0, indicating a weak relationship.
Measuring Correlation
There are several methods to measure correlation, the most common of which is the Pearson correlation coefficient. Other methods include the Spearman rank correlation and the Kendall rank correlation, which are better suited for non-linear or ordinal data.
1. Pearson Correlation Coefficient
The Pearson correlation coefficient (r) is a measure of linear correlation between two variables. It ranges from -1 to 1, where:
- A value of +1 indicates a perfect positive linear relationship.
- A value of -1 indicates a perfect negative linear relationship.
- A value of 0 indicates no linear relationship.
The Pearson correlation formula is as follows:
![\[ r = \frac{\sum (x - \bar{x})(y - \bar{y})}{\sqrt{\sum (x - \bar{x})^2 \sum (y - \bar{y})^2}} \]](https://www.sridianti.com/wp-content/uploads/2024/10/quicklatex.com-0655a511851bf58750c1db94737356b8_l3.png "Rendered by QuickLaTeX.com")
Where:
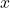and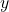 
are the values of the two variables.
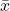and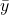 
are the means of the two variables.
Example Calculation of Pearson Correlation:
Consider two variables, study hours and test scores, for a sample of students. Suppose we have the following data:
- Study hours: [2, 4, 6, 8]
- Test scores: [50, 60, 70, 80]
Using the Pearson formula, we can calculate the correlation coefficient (r) to see if there is a positive correlation between study hours and test scores.
2. Spearman Rank Correlation
The Spearman rank correlation is a non-parametric measure of rank correlation. It assesses how well the relationship between two variables can be described using a monotonic function. This method is used when data does not meet the requirements for Pearson correlation, especially with ordinal data or non-linear relationships.
Interpretation of Correlation in Real Life
Correlation is highly useful in identifying and understanding relationships between variables in real life. Here are some examples to illustrate its application in various fields.
Example 1: Correlation in Business
Marketing expenditure and sales: A business wants to determine if there is a correlation between the amount it spends on marketing and its sales revenue. By analyzing past data, the business finds a strong positive correlation between marketing expenditure and sales, indicating that higher marketing spending is associated with increased sales. This insight allows the business to allocate resources more effectively, knowing that investing in marketing can positively impact sales performance.
Example 2: Correlation in Healthcare
Smoking and lung disease: Researchers frequently study the correlation between smoking and lung disease. Numerous studies show a strong positive correlation between the number of cigarettes smoked and the likelihood of developing lung disease. This information helps in public health campaigns aimed at reducing smoking rates to prevent lung-related illnesses.
Example 3: Correlation in Education
Study time and academic performance: In education, understanding the correlation between study time and grades is valuable. Research often finds a positive correlation between the number of hours a student spends studying and their grades. This insight helps educators encourage effective study habits, as data supports the idea that increased study time can improve academic performance.
Example 4: Correlation in Economics
Interest rates and inflation: Economists often analyze the correlation between interest rates and inflation. A negative correlation is often observed, meaning that as interest rates increase, inflation tends to decrease. Central banks use this relationship to make monetary policy decisions, raising interest rates to control inflation or lowering them to stimulate economic growth.
Limitations of Correlation
While correlation is a valuable statistical tool, it is important to understand its limitations and not to misinterpret or misuse correlation coefficients.
1. Correlation Does Not Imply Causation
A common misconception is that correlation implies causation, but this is not true. Correlation only indicates a relationship between variables; it does not prove that one variable causes the other. For instance, there might be a positive correlation between ice cream sales and drowning incidents, but this does not mean that eating ice cream causes drowning. Instead, both variables may be influenced by a third factor—in this case, warmer weather.
2. Impact of Outliers
Outliers, or extreme values in the data, can significantly impact the correlation coefficient, making it appear stronger or weaker than it is. Outliers can distort the interpretation of correlation, especially in small data sets, so it is essential to handle or remove them appropriately when analyzing data.
3. Non-Linear Relationships
The Pearson correlation coefficient only measures linear relationships. If two variables have a non-linear relationship, the correlation coefficient may not accurately represent their association. For example, a quadratic relationship between two variables might show no correlation even though they have a clear pattern. In such cases, other statistical methods, such as regression analysis, may be more appropriate.
4. Correlation in Small Samples
In small data sets, correlation coefficients can be unstable and may not provide an accurate representation of the relationship between variables. Larger samples typically provide more reliable estimates of correlation.
Examples Illustrating Misinterpretation of Correlation
Example 1: Correlation Between Coffee Consumption and Productivity
Suppose a company finds a positive correlation between coffee consumption and employee productivity. However, this does not necessarily mean that drinking more coffee causes increased productivity. It is possible that employees who are more productive also tend to drink coffee, or that other factors, like work environment or motivation, influence both productivity and coffee consumption. Misinterpreting this correlation could lead to false conclusions about the impact of coffee on productivity.
Example 2: Correlation Between Social Media Use and Anxiety
A study finds a correlation between increased social media use and higher anxiety levels. While this suggests a relationship, it does not mean that social media use directly causes anxiety. It could be that individuals who are already more anxious are more likely to spend time on social media. Without further analysis, it is impossible to determine the cause-and-effect relationship between these variables.
Conclusion
Correlation is a powerful statistical tool that helps identify and measure the strength of relationships between variables, offering valuable insights for data analysis across various fields. The main types of correlation—positive, negative, and none—describe the nature of relationships between variables. Using correlation coefficients, we can quantify these relationships and use them to make informed decisions in fields like business, healthcare, education, and economics.
While correlation is essential for identifying relationships, it’s important to remember that correlation does not imply causation. Misinterpreting correlation can lead to incorrect conclusions, especially when outliers, small samples, or third variables influence the data. By understanding the strengths and limitations of correlation, we can effectively use it to uncover meaningful patterns in data and make well-informed decisions.
