In mathematics, functions are central to describing relationships between elements of two sets. Functions map elements from one set, called the domain, to another set, called the codomain. Within the codomain, some elements are “reachable” from the domain through the function, forming what is known as the range. Understanding these concepts—domain, codomain, and range—is essential in defining and working with functions. This article will explore each concept in detail, with examples to illustrate how they function individually and as part of the whole.

What Is the Domain of a Function?
The domain of a function is the complete set of all possible input values (or arguments) for which the function is defined. In simpler terms, it is the collection of all values that can be plugged into the function to produce a valid output.
For example, if we have a function ![]() , then the domain of
, then the domain of ![]() consists of all real numbers because squaring any real number will produce a valid result. However, for other functions, like
consists of all real numbers because squaring any real number will produce a valid result. However, for other functions, like ![]() , the domain excludes
, the domain excludes ![]() because dividing by zero is undefined.
because dividing by zero is undefined.
Example 1: Domain of Basic Functions
Consider the function ![]() .
.
- Analysis: Since square roots are only defined for non-negative numbers in the real number system,
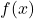 is defined only for
is defined only for 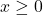 .
. - Domain: The domain of
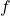 is all non-negative real numbers, or
is all non-negative real numbers, or 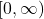 .
.
If instead we have a function ![]() (the natural logarithm), the domain is restricted to
(the natural logarithm), the domain is restricted to ![]() because the logarithm is only defined for positive values.
because the logarithm is only defined for positive values.
- Domain:
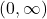
These examples show that the domain depends on the specific function and the operations involved within it.
Example 2: Domain of a Rational Function
Consider the function ![]() .
.
- Analysis: This function is defined for all real numbers except where the denominator is zero.
- Domain: To find the domain, set the denominator equal to zero and solve:
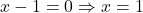 .
. - Result: The domain of
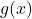 is all real numbers except
is all real numbers except 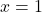 , or
, or 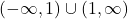 .
.
For rational functions, the domain typically excludes values that would make the denominator zero, as division by zero is undefined.
What Is the Codomain of a Function?
The codomain of a function is the set in which all the outputs of the function lie. It is specified when defining the function and represents the “target” space that the function maps to, whether or not all elements in the codomain are actually reached by the function.
The distinction between codomain and range is essential: while the range is the set of all actual outputs, the codomain is the set of all possible outputs by definition, as stated in the function.
Example 1: Specifying the Codomain
Consider the function ![]() defined as
defined as ![]() , where
, where ![]() represents the set of real numbers.
represents the set of real numbers.
- Codomain: Here, the codomain is all real numbers,
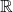 , even though the function
, even though the function 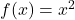 only produces non-negative values for all real
only produces non-negative values for all real 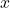 .
.
In this case, the codomain of ![]() is
is ![]() , but the range (the set of actual outputs) is
, but the range (the set of actual outputs) is ![]() .
.
Example 2: Different Codomains for the Same Function
Now, consider the same function ![]() , but redefine it as
, but redefine it as ![]() .
.
- Codomain: Here, we have redefined the codomain to be the set of all non-negative real numbers,
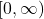 , which now matches the range of the function.
, which now matches the range of the function.
This example illustrates that while the codomain is part of the function definition, it is separate from the range, which depends on the values the function can actually produce.
What Is the Range of a Function?
The range of a function is the set of all actual outputs the function can produce. It consists only of those values in the codomain that the function reaches for at least one input from the domain.
In many cases, the range is a subset of the codomain, particularly if the function doesn’t reach every element of the codomain.
Example 1: Range of a Quadratic Function
Consider the function ![]() , defined as
, defined as ![]() .
.
- Range: Since
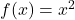 produces only non-negative values (e.g.,
produces only non-negative values (e.g., 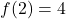 ,
, 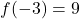 ), the range of
), the range of 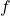 is the set of non-negative real numbers, or
is the set of non-negative real numbers, or 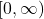 .
. - Codomain: The codomain of this function, however, is all real numbers
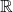 , as specified in the function definition.
, as specified in the function definition.
This example highlights that the range of ![]() (the set of outputs) is a subset of the codomain.
(the set of outputs) is a subset of the codomain.
Example 2: Range of a Trigonometric Function
Consider the sine function ![]() , defined as
, defined as ![]() .
.
- Range: The sine function oscillates between -1 and 1, so the range of
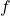 is
is ![Rendered by QuickLaTeX.com [-1, 1]](https://www.sridianti.com/wp-content/uploads/2024/11/quicklatex.com-61888feeeeb8e122a17b229740cd3b65_l3.png) , which in this case matches the codomain.
, which in this case matches the codomain.
By defining the codomain as ![]() , we align it with the range, as sine values cannot exceed these limits. This is common in trigonometric functions, where the range is bounded by the properties of the function.
, we align it with the range, as sine values cannot exceed these limits. This is common in trigonometric functions, where the range is bounded by the properties of the function.
Why Are Domain, Codomain, and Range Important?
Understanding domain, codomain, and range is essential because they provide crucial information about how a function behaves and interacts with different sets.
1. Domain: Helps us understand the limitations on the input values for a function.
2. Codomain: Defines the “target” set that the function maps to, helping to clarify expectations about the possible outputs.
3. Range: Shows the actual outputs, indicating which elements of the codomain are reached by the function and highlighting any unused portions of the codomain.
These distinctions become especially important in advanced mathematics, calculus, and computer science, where precise definitions are necessary to avoid ambiguities in problem-solving and applications.
Working with Domain, Codomain, and Range in Real-World Applications
1. Physics: Describing Motion and Energy
Functions are widely used in physics to describe various phenomena, such as motion, energy, and force.
Example: The kinetic energy of an object is given by the function ![]() , where
, where ![]() is the mass (a constant) and
is the mass (a constant) and ![]() is the velocity.
is the velocity.
- Domain: Since velocity
 can take any real value, the domain is
can take any real value, the domain is 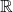 .
. - Codomain: Defined as all real numbers,
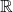 , but realistically, we only consider non-negative kinetic energy.
, but realistically, we only consider non-negative kinetic energy. - Range: For non-zero mass,
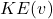 produces only non-negative values, so the range is
produces only non-negative values, so the range is 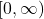 .
.
This example illustrates how understanding the domain, codomain, and range can provide insight into the physical properties of a function and its applications.
2. Economics: Modeling Supply and Demand
In economics, functions model relationships between variables like price, supply, and demand.
Example: Suppose the demand for a product is given by ![]() , where
, where ![]() is the price and
is the price and ![]() represents demand.
represents demand.
- Domain: Since price
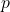 must be non-negative, the domain is
must be non-negative, the domain is 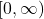 .
. - Codomain: Set as
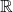 , representing all real values.
, representing all real values. - Range: As
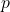 increases,
increases, 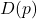 decreases. If
decreases. If  , then
, then  , which makes sense if we restrict the range to non-negative values of demand, resulting in the range
, which makes sense if we restrict the range to non-negative values of demand, resulting in the range ![Rendered by QuickLaTeX.com [0, 100]](https://www.sridianti.com/wp-content/uploads/2024/11/quicklatex.com-818b9662ae704234d95a3cea6756bd8d_l3.png) .
.
By analyzing the function’s domain and range, we can gain a better understanding of the relationship between price and demand.
3. Biology: Modeling Population Growth
Functions also model population growth, helping biologists understand species dynamics in ecosystems.
Example: The exponential growth model ![]() , where
, where ![]() is the initial population and
is the initial population and ![]() is the growth rate.
is the growth rate.
- Domain: Since
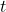 represents time, the domain is
represents time, the domain is 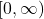 .
. - Codomain: All real numbers, but practically only non-negative values make sense.
- Range: Since
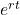 is always positive for real
is always positive for real  and
and 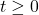 , the range is
, the range is 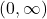 .
.
The domain and range constraints provide essential context for interpreting population growth realistically.
Conclusion
The concepts of domain, codomain, and range are foundational in understanding functions in mathematics and their applications in real life. The domain sets the limitations on input values, the codomain specifies the possible output space, and the range identifies the actual outputs. By examining examples across various fields, we see that understanding these three elements helps clarify how functions behave, making it easier to apply them accurately in science, engineering, economics, and beyond. Through the proper use of domain, codomain, and range, we gain a more thorough understanding of mathematical relationships and their implications in the real world.