Understanding Frequency, Time Period, and Angular Frequency: Definitions, Relationships, and Applications

In physics, frequency, time period, and angular frequency are fundamental concepts used to describe oscillatory motion, wave behavior, and circular motion. These concepts are essential for understanding how objects oscillate, how waves propagate, and how rotational systems behave. Frequency and time period describe the rate and duration of cycles in a repeating motion, while angular frequency specifically applies to rotational motion, measuring the rate at which an object rotates in terms of angles. Together, these concepts are critical in fields such as mechanical engineering, electrical engineering, signal processing, and even biology.

This article delves into the definitions, relationships, and practical applications of frequency, time period, and angular frequency, with examples that illustrate their importance in both theoretical and real-world scenarios.

What Is Frequency?

Frequency is the number of times an event repeats within a specific time period. In the context of oscillatory motion, frequency refers to the number of cycles or complete oscillations that occur in one second. It is commonly used to describe waves, sound, vibrations, and any periodic motion.

Definition and Units

The frequency of a repeating event is defined as the number of cycles per second. In mathematical terms:

$f = \frac{N}{T}$

where:

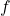$f$ is the frequency,
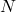$N$ is the number of cycles,
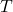$T$ is the total time.

The SI unit for frequency is the hertz (Hz), where 1 Hz is equivalent to one cycle per second. For example, if a wave oscillates 60 times in a second, its frequency is 60 Hz. Higher frequencies indicate more rapid oscillations, while lower frequencies represent slower oscillations.

Examples of Frequency

1. Sound Waves: Frequency determines the pitch of a sound. For instance, a low-frequency sound wave (e.g., 100 Hz) produces a low pitch, while a high-frequency wave (e.g., 1000 Hz) produces a high pitch.

2. Electricity: In alternating current (AC) circuits, the frequency of the current determines the rate at which the current alternates. For example, in many countries, household AC power has a frequency of 50 or 60 Hz, meaning the current alternates direction 50 or 60 times per second.

3. Radio Waves: Frequency is crucial in telecommunications, where different frequencies are used to transmit radio, television, and mobile phone signals. For example, FM radio stations typically broadcast at frequencies between 88 MHz and 108 MHz.

What Is the Time Period?

The time period (often simply called “period”) is the duration of time it takes for one complete cycle or oscillation of a repeating event to occur. It is the inverse of frequency, meaning that a higher frequency corresponds to a shorter time period, and vice versa.

Definition and Units

The time period, denoted as $T$ , is defined as the time taken for one complete cycle of oscillation. Mathematically, it is given by:

$T = \frac{1}{f}$

where $f$ is the frequency. This relationship shows that as frequency increases, the time period decreases, and as frequency decreases, the time period increases.

The SI unit for the time period is the second (s). For example, if a wave has a frequency of 2 Hz, its time period is:

$T = \frac{1}{2 \, \text{Hz}} = 0.5 \, \text{seconds}$

This means that each cycle of the wave takes 0.5 seconds to complete.

Examples of Time Period

1. Pendulum Motion: A simple pendulum swinging back and forth has a time period, which depends on its length and gravity. For example, if the time period of a pendulum is 2 seconds, it takes 2 seconds for the pendulum to complete one full swing (from one side to the other and back again).

2. Rotating Objects: The time period can also describe the rotation of objects. For instance, if a wheel rotates 10 times in one second, the frequency is 10 Hz, and the time period is 0.1 seconds, meaning it takes 0.1 seconds for the wheel to complete one rotation.

3. Earth’s Rotation: The Earth takes approximately 24 hours to complete one rotation on its axis, so the time period of the Earth’s rotation is about 24 hours. In this case, the frequency of Earth’s rotation is very low.

What Is Angular Frequency?

Angular frequency, often denoted by the symbol $\omega$ , describes the rate of rotation or oscillation in terms of angles, typically in circular or rotational motion. It represents how fast an object travels through an angle or how quickly a repeating motion occurs within a given time frame, measured in radians per second (rad/s).

Angular frequency is closely related to linear frequency, but while frequency counts the number of cycles per second, angular frequency considers the rate of angle change per second. One full cycle or oscillation corresponds to an angle of $2\pi$ radians.

Definition and Formula

Angular frequency $\omega$ is calculated as:

$\omega = 2 \pi f$

where:

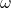$\omega$ is the angular frequency,
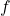$f$ is the linear frequency in hertz (cycles per second).

Since $f = \frac{1}{T}$ , angular frequency can also be expressed in terms of the time period:

$\omega = \frac{2 \pi}{T}$

This formula shows that angular frequency is directly proportional to frequency. Higher angular frequencies correspond to faster rotations or oscillations.

Examples of Angular Frequency

1. Rotating Wheel: Consider a wheel rotating at a frequency of 5 Hz. The angular frequency of the wheel’s rotation is:

$\omega = 2 \pi \times 5 = 10 \pi \, \text{rad/s}$

This means the wheel rotates through $10 \pi$ radians per second.

2. Mass-Spring System: In a mass-spring system undergoing simple harmonic motion, the angular frequency depends on the mass ( $m$ ) and the spring constant ( $k$ ):

$\omega = \sqrt{\frac{k}{m}}$

For a system with a spring constant of 100 N/m and a mass of 1 kg, the angular frequency is:

$\omega = \sqrt{\frac{100}{1}} = 10 \, \text{rad/s}$

3. Circular Motion of a Planet: When a planet orbits the Sun, its angular frequency depends on the time it takes to complete one orbit (its time period). For instance, if Earth takes about 365 days to orbit the Sun, we can calculate its angular frequency as follows:

$T = 365 \times 24 \times 3600 \approx 3.15 \times 10^7 \, \text{seconds}$

$\omega = \frac{2 \pi}{T} \approx \frac{2 \pi}{3.15 \times 10^7} \approx 2 \times 10^{-7} \, \text{rad/s}$

This low angular frequency reflects the slow but continuous orbit of Earth around the Sun.

Relationships Between Frequency, Time Period, and Angular Frequency

Frequency, time period, and angular frequency are closely related, as they all describe aspects of periodic motion. Understanding the relationships between them helps us analyze oscillatory systems and circular motion more effectively.

1. Frequency and Time Period: These two quantities are inversely related:

$f = \frac{1}{T} \quad \text{and} \quad T = \frac{1}{f}$

This means that if the frequency of an oscillation increases, the time period decreases proportionally, and vice versa.

2. Frequency and Angular Frequency: Angular frequency is directly proportional to linear frequency:

$\omega = 2 \pi f$

If the frequency of an oscillation doubles, the angular frequency also doubles. This relationship is particularly useful when analyzing rotational and wave motion, where angles are involved.

3. Time Period and Angular Frequency: Angular frequency is inversely related to the time period:

$\omega = \frac{2 \pi}{T}$

A shorter time period results in a higher angular frequency, indicating faster rotations or oscillations.

Practical Applications

Understanding frequency, time period, and angular frequency is crucial in many fields, including physics, engineering, and telecommunications. Some notable applications include:

Electromagnetic Waves: In radio and television broadcasting, frequency is used to modulate signals. Radio stations broadcast at specific frequencies, such as 98.7 MHz or 101.5 MHz, to allow listeners to tune in to a specific channel.
Mechanical Vibrations: Engineers design buildings, bridges, and other structures to avoid resonant frequencies that could lead to excessive vibrations and structural damage. Knowledge of angular frequency and time period helps engineers calculate safe designs.
Medical Imaging: Magnetic Resonance Imaging (MRI) relies on radiofrequency pulses and the resonant frequencies of atomic nuclei in the human body. Understanding frequency and angular frequency is essential in generating clear MRI images for medical diagnosis.
Simple Harmonic

Motion: Systems like pendulums, springs, and oscillating masses can be analyzed using frequency, time period, and angular frequency to predict behavior and design applications, such as timing devices.

Example Calculations

1. Calculating Frequency from Time Period

If a pendulum has a time period of 2 seconds, its frequency is:

$f = \frac{1}{T} = \frac{1}{2} = 0.5 \, \text{Hz}$

2. Calculating Angular Frequency from Frequency

If an AC current has a frequency of 60 Hz, the angular frequency of the current is:

$\omega = 2 \pi f = 2 \pi \times 60 \approx 377 \, \text{rad/s}$

3. Finding Time Period from Angular Frequency

If a rotating fan has an angular frequency of 20 rad/s, its time period is:

$T = \frac{2 \pi}{\omega} = \frac{2 \pi}{20} = 0.314 \, \text{seconds}$

Conclusion

Frequency, time period, and angular frequency are essential concepts in understanding oscillatory and rotational motion. Frequency measures how often an event repeats, the time period measures the time it takes for one cycle, and angular frequency describes the rate of rotation in radians per second. These concepts not only help us analyze simple harmonic motion but also find applications in various fields such as engineering, telecommunications, and medicine. Mastering the relationships and applications of frequency, time period, and angular frequency deepens our understanding of the complex motions observed in the natural world and in technological systems.