Understanding Periodic Motion: Principles, Characteristics, and Examples

Periodic motion is a type of motion that repeats itself at regular intervals of time. This concept is foundational in physics and appears in a wide variety of natural and artificial systems. From the oscillations of a pendulum to the vibrations of a guitar string and the revolution of planets, periodic motion is everywhere. It helps describe and predict the behavior of systems in mechanics, acoustics, and even quantum physics.

This article provides a detailed overview of periodic motion, its mathematical characteristics, different types, and real-world examples to illustrate each concept.

What Is Periodic Motion?

Periodic motion occurs when an object or system moves in such a way that it repeats the same pattern over a fixed period. The key feature of periodic motion is repetition: the motion cycles through identical states at equal intervals of time.

Key Characteristics of Periodic Motion

1. Period ( $T$ ): The time taken for one complete cycle of motion. It is measured in seconds.
– Example: For a clock’s pendulum, the period is the time taken for the pendulum to swing back and forth once.

2. Frequency ( $f$ ): The number of cycles completed per second. It is the reciprocal of the period:

$f = \frac{1}{T}$

Measured in Hertz (Hz).

3. Amplitude: The maximum displacement of the system from its equilibrium position.
– Example: For a vibrating string, the amplitude is the height of the string’s oscillation.

4. Phase: Describes the state of the motion within the cycle at any given time, measured in radians or degrees.

Example: Simple Pendulum

A pendulum exhibits periodic motion as it swings back and forth. Each swing represents one complete cycle, with the time for one cycle defining the period. The frequency is the number of swings per second, while the amplitude is the maximum angle of the swing.

Types of Periodic Motion

Periodic motion can be categorized based on the type of system and the forces involved.

1. Oscillatory Motion

Oscillatory motion is a type of periodic motion in which an object moves back and forth about an equilibrium position under the influence of restoring forces.

Example: Spring-Mass System

In a spring-mass system, a mass attached to a spring oscillates when displaced from its equilibrium position. The restoring force is provided by Hooke’s Law:

$F = -kx$

Where:

$F$ is the restoring force.
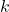$k$ is the spring constant.
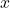$x$ is the displacement.

The motion is periodic, with the period given by:

$T = 2\pi \sqrt{\frac{m}{k}}$

Where $m$ is the mass.

—

2. Rotational Motion

Rotational motion occurs when an object moves in a circular path and completes rotations at regular intervals.

Example: Earth’s Rotation

The Earth’s rotation about its axis is a periodic motion with a period of 24 hours. Each full rotation represents one cycle, and the periodic nature of this motion defines the concept of a day.

—

3. Vibrational Motion

Vibrational motion involves the rapid oscillation of particles about an equilibrium position. This type of periodic motion is common in acoustics and molecular physics.

Example: Vibrating Guitar String

When a guitar string is plucked, it vibrates periodically, producing sound waves with a frequency that corresponds to the pitch of the note.

—

4. Wave Motion

Wave motion, such as sound waves, light waves, or water waves, is inherently periodic. The motion of particles in the medium oscillates periodically as the wave propagates.

Example: Sound Waves

Sound waves are longitudinal waves where air particles oscillate back and forth in a periodic fashion. The frequency of the wave determines the pitch of the sound.

Mathematical Description of Periodic Motion

Periodic motion can be described mathematically using trigonometric functions, particularly sine and cosine. The general equation for periodic motion is:

$x(t) = A \cos(\omega t + \phi)$

Where:

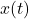$x(t)$ is the displacement at time $t$ .
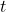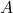$A$ is the amplitude.
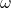$\omega$ is the angular frequency ( $\omega = 2\pi f$ ).
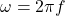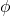$\phi$ is the phase constant, which shifts the motion along the time axis.

Example: Simple Harmonic Motion (SHM)

Simple Harmonic Motion (SHM) is a specific type of periodic motion where the restoring force is directly proportional to displacement:

$F = -kx$

The displacement of the system as a function of time is given by:

$x(t) = A \cos(\omega t)$

Where $A$ is the maximum displacement and $\omega = \sqrt{\frac{k}{m}}$ .

Example of SHM: Swinging Pendulum

For small angular displacements, the motion of a pendulum approximates SHM. The period is given by:

$T = 2\pi \sqrt{\frac{L}{g}}$

Where:

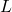$L$ is the length of the pendulum.
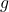$g$ is the acceleration due to gravity.

Energy in Periodic Motion

Periodic motion involves continuous energy exchange between potential and kinetic energy.

1. Potential Energy: Energy stored due to displacement from equilibrium.
– Example: In a spring-mass system, the potential energy at maximum displacement is:

$PE = \frac{1}{2} kx^2$

2. Kinetic Energy: Energy of motion.
– Example: At equilibrium, the spring-mass system’s kinetic energy is:

$KE = \frac{1}{2} mv^2$

3. Total Energy: The total energy remains constant and is the sum of potential and kinetic energy:

$E = KE + PE$

—

Real-World Examples of Periodic Motion

1. Clock Pendulum

A pendulum in a grandfather clock exhibits periodic motion, maintaining consistent time intervals.

Period: Determined by the length of the pendulum.
Application: Accurate timekeeping in mechanical clocks.

—

2. Planetary Orbits

Planets revolve around the sun in nearly circular or elliptical orbits, exhibiting periodic motion.

Period: The time for one complete revolution, as defined by Kepler’s laws of planetary motion.
Example: Earth’s orbit around the sun defines a year.

—

3. Heartbeats

The beating of the human heart is a biological example of periodic motion.

Frequency: The average adult heart beats 60–100 times per minute.
Amplitude: Corresponds to the intensity of the heartbeat.

—

4. AC Current

Alternating current (AC) in electrical circuits changes direction periodically, following a sinusoidal pattern.

Frequency: The standard frequency of AC in most countries is 50 Hz or 60 Hz.
Example: The voltage in household electrical outlets follows periodic motion.

—

5. Swing on a Playground

A child on a swing exhibits periodic motion, moving back and forth around an equilibrium position.

Period: Depends on the length of the swing and gravity.
Example: For a swing with a length of 2 meters, the period is approximately:

$T = 2\pi \sqrt{\frac{2}{9.8}} \approx 2.83 \, \text{seconds}.$

—

Importance of Periodic Motion

Periodic motion is fundamental in understanding and designing systems in various fields:

1. Engineering: Vibrations in mechanical systems are modeled using periodic motion to ensure structural stability.
2. Astronomy: Planetary and celestial motion are analyzed through periodic behavior to predict orbits and eclipses.
3. Music: Sound production and resonance rely on periodic vibrations.
4. Communication: Electromagnetic waves used in radio, television, and cellular networks are periodic in nature.

—

Conclusion

Periodic motion is a cornerstone of physics, describing countless phenomena in nature and technology. Whether it’s the oscillation of a pendulum, the vibration of a guitar string, or the revolution of celestial bodies, periodic motion provides a predictable and repeatable pattern of behavior. By understanding its principles, mathematical representation, and real-world applications, we gain valuable insights into the dynamics of systems that shape our universe and daily lives. The study of periodic motion continues to play a vital role in advancing science, engineering, and technology.