Understanding Relative Speed: Concepts and Examples

Relative speed is a concept in physics and mathematics that deals with the velocity of one object as observed from another moving object. It plays a crucial role in solving problems involving motion, especially when two or more objects move simultaneously. Relative speed simplifies the analysis of complex motion scenarios by focusing on the velocity difference between objects.

In this article, we’ll explore the concept of relative speed, its formulas, and practical applications, with detailed examples to illustrate its use.

What Is Relative Speed?

Relative speed is the rate at which one object moves with respect to another. It depends on the individual speeds and directions of the objects. The concept is commonly applied in scenarios involving two moving objects, such as vehicles, trains, or people, and helps determine how quickly the distance between them changes.

Key Idea

1. When objects move in the same direction: The relative speed is the difference between their speeds.

$\text{Relative Speed} = \lvert v_1 - v_2 \rvert$

Here, $v_1$ and $v_2$ are the speeds of the two objects.

2. When objects move in opposite directions: The relative speed is the sum of their speeds.

$\text{Relative Speed} = v_1 + v_2$

Example 1: Understanding Same-Direction Motion

Two cars are traveling along the same road. Car A has a speed of 60 km/h, and Car B has a speed of 40 km/h. Both cars are moving in the same direction.

Relative speed = 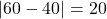$\lvert 60 - 40 \rvert = 20$ km/h.
Interpretation: From Car B’s perspective, Car A appears to be moving away at a speed of 20 km/h.

Example 2: Understanding Opposite-Direction Motion

Now, suppose the same cars are moving toward each other, with Car A traveling at 60 km/h and Car B at 40 km/h.

Relative speed = 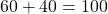$60 + 40 = 100$ km/h.
Interpretation: From the perspective of either car, the other appears to be approaching at a speed of 100 km/h.

Deriving Relative Speed Formula

Relative speed can be derived using basic concepts of motion:

1. For Same-Direction Motion: If two objects are moving in the same direction, the effective speed at which the distance between them changes is the difference in their speeds. Subtracting the slower speed from the faster speed gives the relative speed.

2. For Opposite-Direction Motion: When two objects move toward or away from each other, their speeds combine to give the relative speed. This is because both contribute to the change in the distance between them.

Applications of Relative Speed

Relative speed is widely used in physics, engineering, and transportation planning to solve practical problems involving motion.

1. Solving Distance Problems

Relative speed simplifies calculations of the time required for two objects to meet or pass each other. The formula is:

$\text{Time} = \frac{\text{Distance}}{\text{Relative Speed}}$

Example: Meeting Point of Two Trains

Two trains start from stations 150 km apart. Train A travels at 50 km/h, and Train B travels at 70 km/h toward each other.

Relative speed = 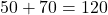$50 + 70 = 120$ km/h.
Time to meet = 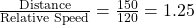$\frac{\text{Distance}}{\text{Relative Speed}} = \frac{150}{120} = 1.25$ hours.

Thus, the trains will meet after 1 hour and 15 minutes.

—

2. Overtaking Problems

When one object overtakes another, relative speed helps determine the time taken to do so.

Example: Car Overtaking a Truck

A car traveling at 80 km/h approaches a truck moving at 60 km/h. The length of the truck is 20 meters. How much time does the car take to overtake the truck?

Relative speed = 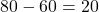$80 - 60 = 20$ km/h = $20 \times \frac{1000}{3600} = 5.56$ m/s.
Distance to cover = Length of the truck = 20 meters.
Time = 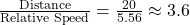$\frac{\text{Distance}}{\text{Relative Speed}} = \frac{20}{5.56} \approx 3.6$ seconds.

The car takes approximately 3.6 seconds to overtake the truck.

—

3. Boat and Stream Problems

In river or stream scenarios, relative speed accounts for the influence of the water current.

Downstream Speed: Speed of the boat + Speed of the current.
Upstream Speed: Speed of the boat – Speed of the current.

Example: Boat in a Stream

A boat can travel at 15 km/h in still water. If the river flows at 5 km/h, calculate the time taken to travel 20 km downstream and upstream.

Downstream speed = 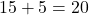$15 + 5 = 20$ km/h.
Upstream speed = 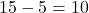$15 - 5 = 10$ km/h.
Time downstream = 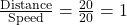$\frac{\text{Distance}}{\text{Speed}} = \frac{20}{20} = 1$ hour.
Time upstream = 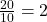$\frac{20}{10} = 2$ hours.

—

4. Relative Motion in Two Dimensions

Relative speed is not limited to linear motion; it also applies to two-dimensional motion, such as airplanes flying in crosswinds or objects moving on inclined planes.

Example: Airplane in a Crosswind

An airplane has an airspeed of 300 km/h and encounters a crosswind blowing at 100 km/h perpendicular to its direction. Find the effective speed of the airplane relative to the ground.

Effective speed = Resultant of the two velocities:

$\text{Effective Speed} = \sqrt{\text{(Airspeed)}^2 + \text{(Wind Speed)}^2} = \sqrt{300^2 + 100^2} = \sqrt{90000 + 10000} = \sqrt{100000} = 316.23 \, \text{km/h}.$

The airplane’s speed relative to the ground is approximately 316.23 km/h.

—

Practical Implications of Relative Speed

1. Traffic Management: Relative speed helps design safer roadways and improve traffic flow by analyzing overtaking scenarios and vehicle spacing.
2. Navigation: In aviation and maritime navigation, relative speed calculations ensure accurate course adjustments in the presence of winds or currents.
3. Sports Analysis: In athletics and racing, relative speed determines the advantage of one competitor over another.
4. Physics Experiments: Relative motion is fundamental in understanding concepts such as frame of reference, velocity addition, and the Doppler effect.

—

Limitations of Relative Speed

While relative speed is a useful concept, it has limitations:

1. Relativity in Higher Speeds: At speeds approaching the speed of light, the classical concept of relative speed breaks down, and Einstein’s theory of relativity must be used.
2. Neglect of Acceleration: Relative speed assumes constant velocities, which may not be realistic in cases involving acceleration or deceleration.
3. Frame of Reference Dependency: The observed relative speed depends on the frame of reference, which can lead to varying interpretations of motion.

—

Conclusion

Relative speed is a fundamental concept in understanding motion, enabling us to analyze how objects move concerning one another. It simplifies calculations of time, distance, and velocity in scenarios involving same or opposite directions, streams, or even two-dimensional motion. By mastering relative speed, we gain insight into the dynamics of moving objects, making it an invaluable tool in physics, engineering, and daily problem-solving. Through real-world examples such as overtaking vehicles, meeting trains, and navigating streams, the utility of relative speed becomes clear in both theoretical and practical contexts.