Resistors are fundamental components in electrical and electronic circuits, used to control the flow of electric current. By combining resistors in series or parallel configurations, engineers and designers can control the current and voltage in different parts of a circuit, enabling various functionalities within electronic devices. Each configuration affects the overall resistance in distinct ways, which in turn impacts the current flow and power distribution within the circuit.

This article explores the concepts of resistors in series and parallel configurations, providing a detailed look at each setup, including real-world examples, calculations, and practical applications. Understanding these configurations is essential for circuit design, as it allows for efficient control of electrical properties.
Resistors in Series Configuration
When resistors are connected in series, they are arranged in a single, continuous path for the current to flow. In a series connection, the total resistance is the sum of each individual resistor’s resistance. This results in an increase in total resistance, which limits the current flow in the circuit.
Properties of Resistors in Series
- Current: The current flowing through each resistor in a series configuration is the same because there is only one path for the current.
- Voltage: The total voltage across the series combination is equal to the sum of the voltages across each individual resistor. This is known as the voltage drop across each resistor, which varies according to the resistance.
- Total Resistance: The total or equivalent resistance in a series configuration is the sum of all individual resistances.
Formula for Total Resistance in Series
If there are three resistors ![]() ,
, ![]() , and
, and ![]() connected in series, the total resistance
connected in series, the total resistance ![]() is given by:
is given by:
![]()
This relationship applies to any number of resistors in series.
Example Calculation for Resistors in Series
Let’s consider a circuit with three resistors connected in series: ![]() ,
, ![]() , and
, and ![]() . Using the formula for total resistance, we find:
. Using the formula for total resistance, we find:
![]()
If the circuit is connected to a 12V battery, the total current ![]() flowing through the circuit can be calculated using Ohm’s law:
flowing through the circuit can be calculated using Ohm’s law:
![]()
Since the current is the same across each resistor in a series circuit, 0.2 A flows through each resistor.
Voltage Drop Across Each Resistor
The voltage drop across each resistor can be calculated by Ohm’s law, ![]() :
:
- Voltage across
 :
: 
- Voltage across
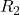 :
: 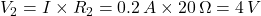
- Voltage across
 :
: 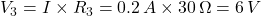
The sum of the voltages across each resistor equals the total applied voltage:
![]()
This confirms that the voltage drops across each resistor in series add up to the total supply voltage.
Applications of Series Resistors
Series resistor configurations are commonly used in circuits requiring precise control of current, such as:
- Voltage dividers: Using resistors in series divides the input voltage into smaller voltages, useful in sensor circuits and analog applications.
- Current Limiting: Series resistors limit the current flow to sensitive components like LEDs, preventing damage due to excessive current.
Resistors in Parallel Configuration
In a parallel configuration, resistors are connected across the same two points, providing multiple paths for the current to flow. In contrast to a series connection, the total or equivalent resistance in a parallel setup is lower than the smallest individual resistance. This allows more current to flow through the circuit, as the overall resistance decreases.
Properties of Resistors in Parallel
1. Voltage: The voltage across each resistor in a parallel configuration is the same, as each resistor is connected directly across the power source.
2. Current: The total current is divided among the parallel resistors based on their resistance values. Resistors with lower resistance carry more current.
3. Total Resistance: The total resistance in a parallel configuration is less than the smallest resistor in the parallel network.
Formula for Total Resistance in Parallel
If there are two resistors ![]() and
and ![]() in parallel, the total resistance
in parallel, the total resistance ![]() is calculated using:
is calculated using:
![]()
For more than two resistors in parallel, the formula generalizes to:
![]()
Example Calculation for Resistors in Parallel
Consider three resistors connected in parallel: ![]() ,
, ![]() , and
, and ![]() . Using the formula for parallel resistance, we calculate
. Using the formula for parallel resistance, we calculate ![]() as follows:
as follows:
![]()
Calculating each term:
![]()
Then, the total resistance is:
![]()
If this parallel network is connected to a 12V source, the total current ![]() flowing through the circuit is:
flowing through the circuit is:
![]()
Current Through Each Resistor
The current through each resistor can be calculated individually using Ohm’s law:
- Current through
 :
: 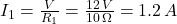
- Current through
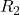 :
: 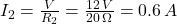
- Current through
 :
: 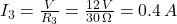
The total current is the sum of the currents through each resistor:
![]()
This confirms that the total current in a parallel circuit is equal to the sum of the individual currents.
Applications of Parallel Resistors
Parallel resistor configurations are useful in circuits where lower overall resistance is needed and where current needs to be divided among multiple components:
- Power Distribution: Parallel configurations allow even distribution of power across multiple devices or components, commonly seen in household electrical wiring.
- Current Sharing: In high-current applications, resistors in parallel can share the load to prevent overheating of a single resistor.
Comparing Series and Parallel Configurations
The choice between series and parallel configurations depends on the intended function of the circuit. Here’s a quick comparison:
| Property | Series Configuration | Parallel Configuration |
|---|---|---|
| Total Resistance | Sum of individual resistances; higher | Less than the smallest resistance; lower |
| Current | Same through each resistor | Divided among resistors, depending on resistance |
| Voltage | Divided across resistors | Same across each resistor |
| Application | Voltage dividers, current limiters | Power distribution, current sharing |
Practical Example: Using Both Series and Parallel Resistors
In some circuits, both series and parallel configurations are used to achieve desired electrical properties. For example, in a household lighting circuit, the lights may be connected in parallel, allowing each light to receive the full supply voltage, while the total circuit current is controlled by a series resistor or circuit breaker.
In electronics, a series-parallel combination can control current in LED arrays. LEDs are arranged in parallel (each branch receiving the same voltage), but a resistor is added in series with each branch to limit the current, protecting the LEDs from excessive current.
Conclusion
Understanding resistors in series and parallel configurations is fundamental for designing and analyzing electrical circuits. Series resistors increase total resistance, which limits current, while parallel resistors decrease total resistance, allowing more current to flow. By combining series and parallel configurations, engineers can achieve precise control over circuit behavior, enabling efficient functionality in various applications, from household appliances to complex electronic devices. Mastery of these configurations allows for creative and optimized circuit designs that meet specific power, voltage, and current requirements.